Точки в параболе

Как обычно в подобных задачах, имеет смысл посмотреть, что происходит при малых значениях чисел, фигурирующих в условии. Уравнения обеих парабол в условии имеют вид \(y^2 = a-x^2\). Как меняется число точек в данной области при малых \(a\)?

Все точки с целыми координатами, находящиеся во внутренней области параболы \(y=2024-x^2\), можно сгруппировать в квадраты и, возможно, один прямоугольник (рис. 2).

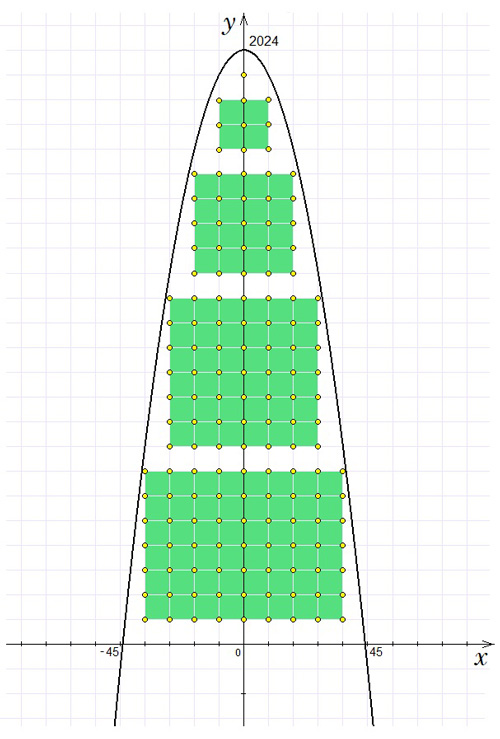
Рис. 2.

Стороны этих квадратов состоят из нечетного количества точек: 1, 3, 5, 7, ..., поэтому искомое число точек будет равно сумме точек в нескольких первых квадратах и еще точек нижнего прямоугольника (которые, по сути, являются несколькими первыми рядами следующего квадрата). Значит, количество целочисленных точек можно выразить так:

где \(n\) — число целых точечных квадратов, \(m\) — число рядов следующего точечного квадрата.

Чтобы выяснить чему равны \(n\) и \(m\) в нашем случае, нужно представить число 2024 в виде суммы максимального числа первых подряд идущих нечетных чисел и числа, которое не превосходит следующего нечетного числа:

Поскольку нас интересуют точки с положительными координатами, \(m=88-1=87\). Число \(n\) легко найти из уравнения \(2n-1=87\), поэтому \(n=44\).

Итак,

Формулу для подсчета суммы квадратов первых \(k\) нечетных чисел \(\sum\limits_{i=1}^k (2i-1)^2\) можно найти, воспользовавшись известной формулой для суммы квадратов начального куска натурального ряда (см., например, задачу Суммы квадратов, суммы кубов...):

Сумма нечетных чисел от 1 до \(2k-1\) — это разность суммы всех чисел от 1 до \(2k-1\) и суммы четных чисел в этом диапазоне:

Первая из этих сумм находится сразу по формуле:

Чтобы найти вторую сумму, вынесем за скобку 2 в квадрате, сдвинем индекс суммирования и применим ту же формулу:

Получим:

При \(k=44\) получим ответ к нашей задаче:

Задачу подсчета узлов координатной плоскости внутри криволинейной трапеции можно обобщить. Пусть функция \(f(x)\) задана на отрезке \([a,\ b]\), где \(a\) и \(b\) — целые числа, тогда подсчет количества точек с целочисленными координатами, находящимися внутри области, ограниченной графиком \(y=f(x)\), и осью \(Ox\) (рис. 3) можно осуществить следующим образом.

Рис. 3.

Напомним, целая часть числа \(r\) — это наибольшее целое число, не превосходящее числа \(r\). Целая часть числа \(r\) обозначается \([r]\), иногда эта операция называется «антье».

Обозначим число узлов внутри такой криволинейной трапеции за \(K\). Тогда \(K\) можно найти по такой формуле:

где число \(g\) — число узлов, находящихся непосредственно на графике функции \(y=f(x)\).

Как устроена эта формула? Для каждого целого \(i\) из отрезка \([a,\ b]\) вычисляется значение \(f(i)\). Обратим внимание, что \([f(i)]\), то  есть целая часть значения функции, совпадает с количеством узлов, лежащих на вертикальной прямой \(x=i\) и одновременно в криволинейной трапеции. Если \(f(i)\) — целое число, то \([f(i)]\) «учитывает» и целую точку на графике функции. Просуммировав все найденные таким образом числа \([f(i)]\), получим сумму, из которой нужно вычесть число \(g\) узлов, лежащих на графике функции \(y=f(x)\).

Для функции, график которой изображен на рис. 3, получим:

Если применить этот прием к решению нашей задачи, то, учитывая, что функция \(y=2024-x^2\) при целых значениях \(x\) принимает только целые значения, можно обойтись без операции «антье». Также можно воспользоваться тем, что график этой функции симметричен относительно оси \(Oy\). В итоге достаточно вычислить \(y(n)=2024-n^2\) для всех целых \(n\) от 0 до \(44=[\sqrt{2024}]\):

Здесь \(g=2\cdot44 +1\), поскольку на верхней границе нашей криволинейной «трапеции», то есть на параболе \(y=2024-x^2\) лежит 89 узлов.

Подставим значения функции:

Раскроем скобки, а затем применим формулу для суммы квадратов:

После всех упрощений получим тот же ответ \(K=121307\).

Для решения нашей задачи можно привлечь и теорему Пика. Эта теорема комбинаторной геометрии позволяет вычислить площадь многоугольника с целочисленными вершинами путем подсчета количества целочисленных точек внутри него (\(B\)) и на его границе (\(\Gamma\)): \(S=B+\frac\Gamma2-1\).

Рассмотрим красный многоугольник, вершинами которого являются узлы, лежащие на параболе (рис. 4). Из формулы Пика можно выразить интересующее нас число \(B=S-\frac\Gamma2+1\). Но для этого нужно знать величины S и Г. Понятно, что на границе этого многоугольника находится \(\Gamma=91+89=180\) узлов.

Рис. 4.

Площадь многоугольника найдем как сумму площадей треугольника \(S_1\) и трапеций \(S_2\), \(S_3\), ..., \(S_{45}\).

Поэтому

Теперь можно вычислить число узлов, находящихся в красном многоугольнике:

Теперь, чтобы получить ответ, осталось вычесть из этого числа количество узлов, лежащих на оси \(Ox\). Получится как раз 121307.