Как расплести косу?
Задача
Из пяти прядей сплетена коса. Верхние концы прядей неподвижно закреплены. Нижние концы прядей могут занимать положения, пронумерованные на рис. 1 цифрами от 1 до 6 (можно считать, что концы фиксируются при помощи канцелярских кнопок). Изначально «заняты» позиции с 1 по 5; концы разных прядей не могут оказаться в одной позиции. Перемещение нижнего конца пряди с одной позиции на другую называется ходом.
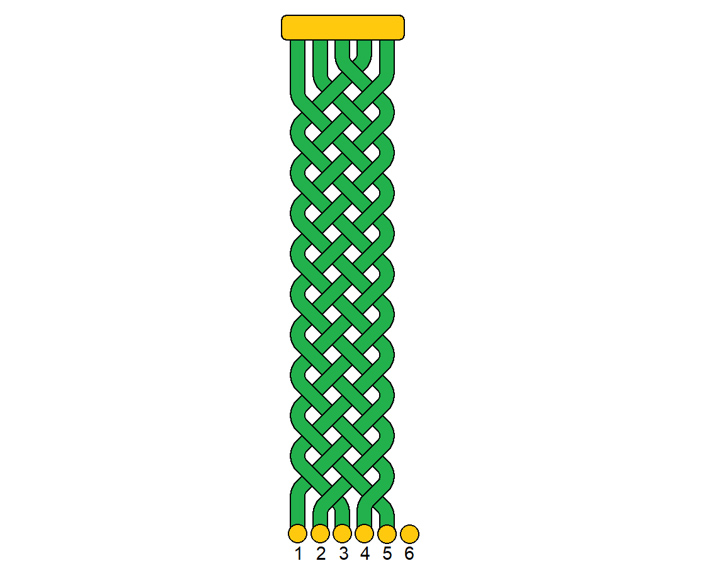
За какое наименьшее число ходов можно расплести косу, то есть добиться положения, в котором никакие две пряди не пересекаются, и при этом их нижние концы по-прежнему занимают позиции с 1 по 5?
Подсказка
Обратите внимание, что основная часть косы периодически повторяется. Значит, в оптимальном решении и некоторая группа ходов будет повторяться.
Решение
Заметим, что ни одно лежащее выше пересечение шнуров не уберется, пока не уберется лежащее ниже. Например, чтобы убрать пересечение D на рис. 2, предварительно нужно убрать пересечение A.

Рис. 2.
Коса содержит десять эквивалентных частей (желтые и голубые на рис. 2). Каждая из них содержит по четыре пересечения прядей. Очевидно, что пересечение A расплетается одним ходом (рис. 3) — переносом пряди с позиции 4 на позицию 6. Далее будем для записи ходов использовать стрелочки: 4→6.

Рис. 3.
Как же быстрее всего расплести четыре пересечения B, C, D и E, расположенные в первой (голубой) части? Очевидным ходом 2→4 расплетается пересечение B. Далее можно расплести пересечение D, но этого делать не имеет смысла, так как появится новое пересечение на месте прежнего узла B, поэтому требуется сделать подготовительный ход 1→2. Следующим ходом 3→1 расплетается пересечение C, а ходом 5→3 расплетается пересечение D. Остается пересечение E, которое одним ходом не убрать, поэтому нужно сделать подготовительный ход 6→5, после чего ходом 4→6 расплетается пересечение E. Все эти перестановки показаны на рис. 4.

Рис. 4.
Таким образом, четыре пересечения B, C, D и E в первой части расплетаются самым экономным способом за 6 ходов: 2-1-3-5-6-4. В этой записи указаны текущие номера переносимых прядей, этого достаточно для однозначного определения порядка ходов, потому что в любой момент имеется одно свободное место. Обратите внимание, что после расплетания пересечений B, C, D и E в первой части свободным остается позиция №4, как и было перед расплетанием. Это значит, что пересечения второй части, отмеченные звездочками (рис. 4, пункт 6), тоже расплетаются за 6 ходов: 2-1-3-5-6-4. За эти же 6 ходов расплетаются пересечения других желтых и голубых частей косы. Таким образом 10 частей косы расплетаются за \(6\cdot 10=60\) ходов.

Рис. 5.
После всех этих манипуляций на косе остается положение, показанное на рис. 5: требуется расплести оставшиеся два пересечения M и N.
Это можно сделать за 3 хода 2-3-5.
Поскольку по условию задачи нижние концы прядей расплетенной косы должны занимать позиции с 1 по 5, придется сделать еще один ход 6→5.
Таким образом, чтобы расплести данную косу, потребуется минимум \(1+6\cdot10+3+1=65\) ходов.

Рис. 6.
Послесловие
В обиходе коса — одна из самых распространенных причесок (и женских, и мужских). Косы плели еще в древности, а сейчас, благодаря услугам парикмахеров, их разнообразие стало поистине неописуемо.
Математики тоже «плетут» косы: существуют математические объекты, которые называются косами. Мы не будем сильно углубляться в теорию кос — раздел математики на стыке алгебры и топологии, занимающийся их изучением. Упомянем лишь, что у математических кос концы прядей закреплены с обеих сторон (в нашей задаче концы были закреплены только с одной стороны, см. рис. 1), поэтому на множестве кос можно ввести специальную операцию («умножение»). Результатом «умножения» двух кос будет новая коса, полученная соединением нижних концов прядей первой косы и верхних концов прядей второй косы. «Умножением» эту операцию называют не случайно. Оказывается, что она сильно напоминает обычное умножение чисел (рациональных или действительных): результатом «умножения» кос снова будет коса (а умножение двух чисел дает снова число), существует коса, «умножение» на которую ничего не меняет (это аналог числа 1; попробуйте понять, как она устроена), для каждой косы есть своя обратная коса («умножение» на которую дает «единичную» косу). Если вы хотя бы немного знаете основы высшей алгебры, то уже поняли, что косы вместе с таким «умножением» образуют группу. Значит, их можно изучать, привлекая аппарат теории групп. С одной стороны это очень мощный инструмент, позволяющий много чего понять и доказать, с другой — теряется наглядность, потому что вместо красивых геометрических объектов приходится иметь дело с абстрактными формулами.
Основы теории кос заложил в первой половине XX века немецкий математик Эмиль Артин. Сейчас она вместе с отчасти родственной теорией узлов прочно вошла в инструментарий современной математики. Родство между косами и узлами показывает теорема Александера (Alexander's theorem): любой узел является замкнутой косой. А математик Вон Джонс (Vaughan F. R. Jones) за свои работы по теории узлов и открытие неожиданных связей со статистической механикой был удостоен Филдсовской премии. Подробнее с основами теорий кос и узлов можно познакомиться в книге А. Б. Сосинского «Узлы и косы».
Головоломку с косой из трех прядей, концы которых скреплены с обеих сторон, я впервые увидел в книге М. Гарднера «Математические досуги» (стр. 147). Там же было указано, что такие косы можно заплетать из большего числа прядей. Имеется в виде следующее: изначально дана «единичная» коса (пряди не переплетены), концы прядей которой закреплены с обеих сторон; требуется (не высвобождая концы) заплести из нее косу (а потом ее расплести обратно).
Изготовить такую головоломку довольно просто: достаточно иметь веревку и пару брусочков. В брусочках нужно просверлить отверстия по числу прядей (я изготовил вариант с пятью прядями), а веревку разрезать на части равной длины. Укрепив концы кусочков веревки в отверстиях так, чтобы не было переплетений (например, при помощи клея) вы получите головоломку (рис. 7).

Рис. 7.
Многочисленные попытки заплести косу из пяти прядей мне не удавались — я уже подумал, что может быть это сделать невозможно. Но как же тогда утверждение из книги Гарднера? Решение придумал мой ученик С. Прика, которому удалось придумать уникальный прием. Чтобы узнать, как это делается, разверните скрытый текст ниже. Но я очень советую попробовать порешать головоломку самостоятельно!
Идея решения
Пронумеруем пряди по порядку и положим головоломку «на ребро» (рис. 8.2). Пряди разделим на две группы: первая с нечетными номерами, вторая — с четными. Раздвинем их так, чтобы получилась «восьмерка», лежащая на боку (рис. 8.3). Затем деревянный брусок правого конца вставим сверху в правое «кольцо» восьмерки (рис. 8.4) и протащим его насквозь (рис. 8.5), при этом стараемся сберечь левое кольцо восьмерки. Затем брусок левого конца проденем через левое «кольцо» восьмерки снизу верх (рис. 8.6–7). Все, косичка заплетена, остается чуть-чуть упорядочить веревочки (рис. 8.8).
-
Простите, чтоб зря не тратить время при разгадывании на недопустимые действия, вопрос:
последовательность
4,1,3... - это можно, это распутываннием считается? Иначе говоря, можно ли проносить кончик "пряди" сзади?
Или только спереди, со стороны наблюдателя?-
Имеется ввиду именно "расплетать косу", то есть проносить кончик пряди сзади нельзя. Вы правильно пишите в конце "переносить только спереди, со стороны наблюдателя".
Я сделал реальную косу, с магнитиками на концах прядей, в которой концы прядей можно переносить с одной позиции на другую со стороны решающего.
-
Заинтриговала речь об умножении - чем последовательно соединение кос схоже с умножением? Ну уж статистическая механика - вообще звучит, как фокус иллюзиониста)
И жаль, что только сказано о них, но не сказано, что именно там такое. Может быть кратенько-популярненько, по Мартин-Гарднеровски, прольёте свет? Ведь явно что-то интересное)
А что касается последнего фото в послесловии - торжественно клянусь, что сделаю такую штуку и найду решение, не заглядывая в ответ!)
Мне кажется, Когда знаешь, что оно есть - поиск решения куда проще, чем если такого знания нет. ))
-
Здесь можно скачать брошюру Сосинского https://www.klex.ru/uz1
Почитайте, там классно написано.
А косичку-головоломку, - сделайте, не пожалеете.
Жаль редактор на Элементах.ру укоротил послесловие, там еще было рассказано, как можно многократно применять описанный прием плетения и показана такая дважды повторенная коса. То есть показан квадрат косы, приведенной в послесловии.
Последние задачи
















Рис. 1.