Объем «линоида»

Попробуйте выяснить, каким уравнением задается поверхность линоида. Возможно, вам удастся установить форму горизонтальных сечений линоида на разной высоте. В этом сильно поможет правильный выбор системы координат.

На рис. 2 показана «раскадровка» образования поверхности линоида в процессе движения отрезка \(KF\). Рассмотрим этот процесс повнимательнее. Если принять, что описанное в условии задачи движение вообще возможно (то есть что при движении длина отрезка \(KF\) не меняется), то происходит следующее. Пока точка \(K\) движется от вершины \(A\) к середине своей диагонали (она, напомним, «ездит» по диагонали \(AC\)), точка \(F\) движется из середины диагонали \(B_1D_1\) к вершине \(B_1\). В тот момент, когда точка \(K\) окажется в середине диагонали \(AC\), точка \(F\) развернется в вершине \(B_1\) и начнет движение к вершине \(D_1\). Когда точка \(K\) «доедет» до вершины \(C\), точка \(F\) будет находиться в середине диагонали \(B_1D_1\) (по-прежнему двигаясь к вершине \(D_1\)). В этот момент пройдена половина цикла. Вторая половина устроена аналогично: точка \(K\) разворачивается в вершине \(C\) и начинает «ехать» к вершине \(A\); в тот момент, когда она будет проходить через середину диагонали \(AC\), точка \(F\) развернется в вершине \(D_1\) и «поедет» обратно к середине диагонали (из которой она и начинала движение). Затем цикл замкнется.

Рис. 2.

На своем пути каждая из точек \(K\) и \(F\) дважды проедет по своей диагонали, а отрезок \(KF\) очертит в пространстве поверхность, которую мы назвали линоидом (рис. 3).

Рис. 3.

Но откуда уверенность, что описанное движение с условием постоянства длины отрезка \(KF\) в принципе возможно? Чтобы это обосновать, вспомним про одну из замечательных кривых — астроиду. Согласно одному из своих определений, она является огибающей семейства отрезков одинаковой длины, концы которых расположены на двух данных перпендикулярных прямых. Ну а то, что все отрезки из такого семейства получаются непрерывным скольжением одного из них так, как показано на анимации слева на рис. 4, достаточно очевидно. Теперь представим, что эти две перпендикулярные прямые — это диагонали \(AC\) и \(BD\), а длина нашего «скользящего» отрезка равна половине диагонали. Обозначим одну из его вершин за \(K\), а из второй опустим перпендикуляр на плоскость противоположной грани куба \(A_1B_1C_1D_1\). Этот перпендикуляр попадет в точности на скрещивающуюся диагональ, обозначим эту точку за \(F\) (рис. 4, справа). В итоге получится именно наш отрезок из условия. Поскольку расстояние между противоположными гранями куба постоянно (и равно длине ребра куба), то по теореме Пифагора длина всех таких отрезков \(KF\) будет одинакова и, если ребро куба принять за \(2a\), равна \(a\sqrt{6}\).

Рис. 4.

Вернемся к поиску объема линоида. Рассмотрим его поверхность в прямоугольной системе координат \(Oxyz\), где \(O\) — центр куба, ось \(Ox\) проходит через середину ребра \(AA_1\), ось \(Oy\) проходит через середину ребра \(BB_1\), а ось \(Oz\) проходит через центр грани \(A_1B_1C_1D_1\) (рис. 5).

Рис. 5.

В этой системе координаты концов отрезка \(KF\) будут иметь такие координаты: \(K(x_K;0;-a)\), \(F(0;y_F;a)\). Пусть произвольная точка \(M\) отрезка \(KF\) имеет координаты \(x;y;z)\), тогда векторы \(\overrightarrow{KM}(x-x_K;y;z+a)\) и \(\overrightarrow{FM}(x;y-y_F;z-a)\) коллинеарны, азначит, их координаты пропорциональны. Поэтому справедливы две пропорции: \(\frac{x-x_K}{x}=\frac{z+a}{z-a}\) и \(\frac{y}{y-y_F}=\frac{z+a}{z-a}\). Из первой пропорции выразим \(x_K=\frac{2ax}{a-z}\), из второй пропорции выразим \(y_F=\frac{2ay}{a+z}\).

По формуле для длины отрезка в пространстве имеем:

Но отрезок \(KF\), как мы уже убедились, имеет постоянную длину \(KF=a\sqrt{6}\), поэтому \(x_K^2+y_F^2+4a^2=6a^2\) или \(x_K^2+y_F^2=2a^2\).

Применяя найденные ранее формулы для \(x_K\) и \(y_F\), получим \(\left(\frac{2ax}{a-z}\right)^2+\left(\frac{2ay}{a+z}\right)^2=2a^2\). После упрощения получим формулу поверхности линоида:

Чтобы получить уравнение горизонтального (то есть перпендикулярного оси \(Oz\)) сечения этого линоида, нужно зафиксировать значение \(z\) в интервале \((-a;\,a)\). Легко видеть, что при фиксированном \(z\) это уравнение превращается в уравнение эллипса с полуосями \(\frac{(a-z)\sqrt2}{2}\) и \(\frac{(a+z)\sqrt2}{2}\). Как известно, площадь эллипса равна произведению длин его полуосей и числа \(\pi\), поэтому площадь нашего эллипса равна

Интегрируя по переменной \(z\) от \(-a\) до \(a\), получим объем линоида:

Эта задача появилась на основе другой задачи, которую я встретил в учебнике по геометрии под редакцией Л. С. Атанасяна. В ней требовалось найти геометрическое место середин отрезков данной длины с концами на двух данных скрещивающихся прямых, угол между которыми равен 90°. Позже выяснилось, что эту задачу предлагали еще на Московской математической олимпиаде 1941 года.

Множество середин таких отрезков образует окружность (рис. 6). Покажем, как это следует из решения основной задачи. Координатная плоскость \(z=0\), которая делит четыре ребра куба пополам, будет делить пополам и все отрезки с концами на диагоналях \(AC\) и \(B_1D_1\), поэтому искомое ГМТ лежит в этой плоскости (легко показать, что точки, не лежащие в этой плоскости, заведомо не подходят). При \(z=0\) уравнение поверхности превращается в уравнение \(\frac{2x^2}{(a-0)^2}+\frac{2y^2}{(a+0)^2}=1\), задающее множество середин всех таких отрезков. Его легко преобразовать к виду \(x^2+y^2=\frac{a^2}{2}\), а это уравнение окружности с центром в точке О и радиусом \(\frac{a\sqrt2}{2}\).

Рис. 6.

Заметим, что если спроецировать отрезок \(KF\) на плоскость \(z=0\) (она же — плоскость \(Oxy\), в ней же лежит «окружность середин»), то его проекции его концов будут скользить по координатным осям \(Ox\) и \(Oy\) так, как показано на рис. 3. А середина его проекции будет двигаться, как мы только что показали, по окружности.

И тут на память приходит известнейшая «кружковская» задача про котенка, который мужественно сидел на прислоненной к стене лестнице, которая начинает скользить по полу и стене: Лестница, стоявшая на гладком полу у стены, соскальзывает вниз. По какой из трех показанных на рис. 7 линий движется котенок, сидящий в середине лестницы?

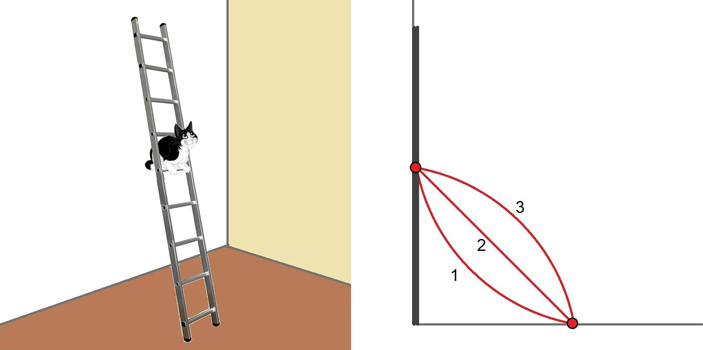
Рис. 7.

Фактически же требуется найти геометрическое место середин отрезков фиксированной длины с концами на сторонах прямого угла. Как мы уже успели показать, это будет часть окружности, но решений этой задачки не требует тяжелой артиллерии в лице метода координат: достаточно свойств диагоналей прямоугольника. Как известно, они равны и точкой пересечения делятся пополам, поэтому отрезок \(KO\) равен половине длины лестницы \(AB\), то есть котенок \(K\) при движении лестницы всегда равноудален от вершины \(O\), то есть движется по дуге \(DF\), являющейся четвертью окружности (рис. 8).

Рис. 8.

Если котенок сидит в точке, отличной от середины лестницы, то он будет двигаться по дуге эллипса (рис. 9). В самом деле, пусть \(AK=a\), \(BK=b\), а переменный угол между лестницей и полом равен \(t\), тогда точка \(K\) имеет координаты \(x=a\cos t\), \(y=b\sin t\). Это — ни что иное как параметрическое задание эллипса, но чтобы получить более привычное уравнение, выразим из этих равенств \(\cos t=\frac xa\), \(\sin t=\frac yb\), возведем их в квадрат и сложим. Учитывая основное тригонометрическое тождество, получим уравнение \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\). Это уравнение эллипса, полуосями которого являются отрезки \(AK\) и \(BK\).

Рис. 9.

Что касается основной задачи, то объем тела можно было бы вычислить, воспользовавшись формулой Симпсона: \(V=\frac{h}{6}(S_0+4S+S_1)\), где \(h\) — высота тела, \(S_0\) и \(S_1\) — площади верхнего и нижнего оснований, а \(S\) — площадь «среднего» сечения, которое параллельно основаниям и равноудалено от них. Для линоида \(h=2a\), его основаниями являются отрезки, поэтому \(S_0=S_1=0\), а серединным сечением является круг радиуса \(\frac{a\sqrt2}{2}\), площадь которого равна \(S=\frac{\pi a^2}2\). По формуле Симпсона получим \(V=\frac{2a}6\left(0+4\cdot\frac{\pi a^2}2+0\right)=\frac{2\pi a^3}3\). Вообще, формула Симпсона предназначена для приближенного вычисления, но в нашем случае она дает точное значение объема, потому что площадь горизонтального сечения является квадратичной формой.

Линоид обладает еще одним интересным свойством. Оказывается, что он равновелик эллипсоиду \(2x^2+2y^2+z^2=a^2\). Это можно обосновать, опираясь на принцип Кавальери. Высота эллипсоида равна ребру куба \(2a\) и любая плоскость, параллельная основанию куба, пересекает линоид по эллипсам, площади которых равны площадям соответствующих кругов (рис. 10). Исключение составляют граничные сечения в верхнем и нижнем положениях, когда сечениями линоида являются отрезки, а сечениями эллипсоида являются точки, но их площади очевидно в обоих случаях равны нулю. Поскольку объем эллипсоида вычисляется по формуле \(V=\frac43\pi ABC\), где \(A\), \(B\) и \(C\) — его полуоси, в данном случае равные \(A=\frac{a}{\sqrt{2}}\), \(B=\frac{a}{\sqrt{2}}\), \(C=a\), то объем нашего эллипсоида равен \(\frac43\pi \cdot \frac{a}{\sqrt{2}} \cdot \frac{a}{\sqrt{2}} \cdot a = \frac{2\pi a^3}{3}.\) Это дает еще одно решение задачи об объеме линоида.

Рис. 10.