Кривые постоянной ширины

Свойство кривой иметь постоянную ширину можно переформулировать. Вспомним, что проекция такой кривой на любое направление — это отрезок, причем его длина не зависит от направления. Если провести через концы отрезка две перпендикулярных ему прямые, то получится, что кривая «зажата» между ними (каждая из них будет касаться кривой; см. рис. 4). При этом расстояние между прямыми равно в точности ширине кривой.

Рис. 4. Параллельные опорные прямые «зажимают» кривую

Вообще, прямая, которая имеет с кривой общие точки, и при этом кривая вся (кроме этих общих точек) лежит в одной полуплоскости относительно этой прямой, называется опорной. Ясно, что есть только две опорные прямые с данным направлением, как раз они и «зажимают» нашу кривую. Используя только что введенное понятие, получаем такую переформулировку: если кривая имеет постоянную ширину, то расстояние между любыми двумя параллельными опорными прямыми равно ширине кривой (рис. 5).

Рис. 5. Если кривая имеет постоянную ширину d, то расстояние между параллельными опорными прямыми не зависит от направления и равно d

Это означает, что мы можем покатить кривую по одной из двух параллельных опорных прямых, а она при этом будет катиться и по второй прямой — ровно так же, как это делает обычная окружность.

Эти замечания делают кривые постоянной ширины чуть более «осязаемыми». В частности, становится понятно, что их можно попытаться составить из дуг окружностей (чтобы было проще катиться).

Самое простое нетривиальное (то есть не окружность) решение — это треугольник Рело, названный по имени придумавшего его немецкого математика Франца Рело (Franz Reuleaux, 1829–1905). Он получится, если в равностороннем треугольнике соединить концы каждой стороны дугой окружности, центр которой находится в противолежащей этой стороне вершине (рис. 6).

Рис. 6. Построение треугольника Рело

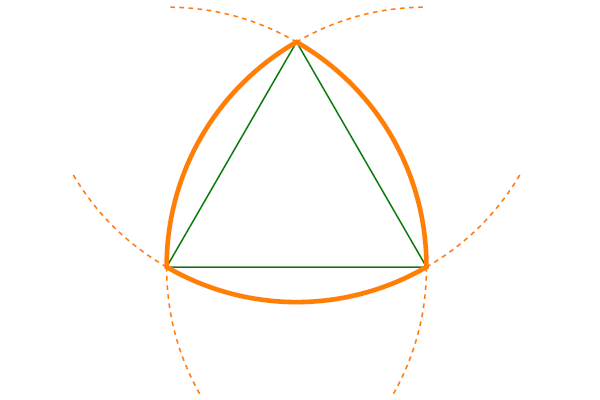
Нетрудно убедиться, что этот криволинейный треугольник действительно имеет постоянную ширину. В самом деле, одна из двух параллельных опорных прямых будет касаться одной из дуг, а вторая будет проходить через противолежащую вершину. Расстояние между ними равно радиусу окружности, то есть оно не зависит от выбора направления.

Рис. 7. Британские монеты достоинством 50 пенсов имеют форму семиугольника Рело. На фото: монета 2005 года выпуска, посвященная 250-й годовщине выхода в свет толкового словаря английского языка Сэмюэля Джонсона

Можно построить и другие примеры линий постоянной ширины: возьмем вместо треугольника любой правильный многоугольник с нечетным числом сторон и соединим концы каждой стороны дугами аналогично предыдущему построению. Получится криволинейный многоугольник Рело. Любопытно, что форму семиугольников Рело имеют британские 20 и 50 (рис. 7) пенсов, некоторые монеты Ботсваны и Иордании.

Рис. 8. Построение кривой постоянной ширины на данном наборе попарно пересекающихся прямых

Рис. 9. «Раздутый» треугольник Рело

Но и на этом примеры таких линий не заканчиваются! Предположим, что на плоскости нарисованы несколько попарно пересекающихся прямых. Любая пара прямых разбивает плоскость на четыре сектора. Выберем один из секторов и проведем дугу окружности произвольного (но достаточно большого, чтобы все точки пересечения прямых лежали внутри окружности) радиуса с центром в вершине сектора от одной его стороны до другой (рис. 8). Дойдя до границы, мы переместимся в соседний сектор. Продолжая линию, соединим и его стороны дугой окружности. Ее центр — вершина сектора, а радиус равен расстоянию от вершины до точки пересечения предыдущей дуги со стороной этого сектора. Этот процесс в конце концов вернет нас в первый сектор, и при этом кривая замкнется (подумайте, почему). Например, таким способом можно получить "раздутый" треугольник Рело (рис. 9).

У линий постоянной ширины есть интересные свойства, как чисто теоретические, так и «прикладные», благодаря которым в некоторых механизмах используются детали такой формы. Отметим, что по теореме Барбье все фигуры ширины d имеют периметр πd (имеются в виду именно фигуры, у которых граница — линия постоянной ширины). Понятное, но при этом нетривиальное доказательство этой теоремы можно прочитать здесь (к сожалению, на английском). Можно доказать, что среди кривых данной постоянной ширины окружность ограничивает максимальную площадь, а треугольник Рело — минимальную.

Поместим треугольник Рело ширины d в квадрат со стороной d. Оказывается, что, независимо от того, как мы это сделаем, он будет касаться сторон квадрата ровно в трех точках (рис. 10, слева). Теперь начнем двигать треугольник внутри квадрата и все время закрашивать область, которую он занимает. Через некоторое время увидим, что незакрашенными остались лишь небольшие кусочки рядом с углами квадрата, а вся остальная его площадь закрашена (рис. 10, справа).

Рис. 10. Треугольник Рело внутри квадрата (слева). При вращении треугольник Рело заметает почти весь квадрат

На этом наблюдении основан способ сверления почти квадратных отверстий. Если взять сверло в форме треугольника Рело и двигать его ось по специальной траектории, то оно просверлит отверстие очень близкое к квадратному. Основную сложность здесь представляет именно соблюдение нужной траектории оси сверла. Но в начале прошлого века с этой проблемой справились, и с тех пор люди с успехом сверлят квадратные отверстия.

Как раз из-за того, что при вращении многоугольников Рело их центр описывает весьма замысловатую траекторию, мы не видим на улицах колес такой формы — изготовление втулок и передач слишком затратное. Куда проще иметь дело с привычными для нас круглыми колесами, ведь при их вращении ось остается неподвижной. Но в принципе колеса могут быть и не круглыми (рис. 11), и при езде пассажир не будет испытывать лишней тряски и дискомфорта. Это прекрасно продемонстрировал китаец Гуань Байхуа, построив вот такой велосипед.

Рис. 11. Сборка этого велосипеда с колесами в виде многоугольников Рело заняла у жителя Китая Гуаня Байхуа полтора года. Фото с сайта www.china.org.cn

Форму, близкую к треугольнику Рело, имеет ротор в двигателе внутреннего сгорания Ванкеля. У такого двигателя есть ряд преимуществ перед двигателями внутреннего сгорания: из-за более простой конструкции и меньшего количества движущихся деталей двигатели Ванкеля получаются компактнее и легче аналогичных по мощности ДВС; они меньше подвержены вибрациям и поэтому более комфортны. При этом на первых порах серьезными проблемами были износоустойчивость, перегрев, высокий расход топлива и токсичность выхлопов. Но на сегодняшний день благодаря использованию современных материалов все они в той или иной степени решены. Сейчас двигатели Ванкеля ставят на автомобили Mazda RX-8.

Советуем зайти на сайт «Математические этюды», где можно не только прочитать много интересного о линиях постоянной ширины и их применениях, но и посмотреть красивые и информативные видео о них.