Улучшенная версия атомно-силового микроскопа рассказала много нового про белок титин

Биофизики давно изучают механические свойства белка титина, играющего важную роль в работе мышечных волокон. Однако до сих пор экспериментальные данные и результаты молекулярного моделирования не удавалось сравнить напрямую, поскольку они отвечали совершенно разным условиям. Группа исследователей из Марселя и Барселоны реализовала новую экспериментальную методику, которая перекинула мостик через эту пропасть и впервые позволила сравнить эти два метода исследования. Полученные результаты улучшили понимание как самого белка, так и теоретических моделей.
Титин
В работе мышечных волокон принимает участие множество белковых молекул (рис. 1), и каждая из них играет свою важную роль (см. краткий обзор в недавней новости «Поворот и замок»: новая модель мышечного сокращения, «Элементы», 05.04.2013). В связи с важностью и сложностью этого процесса исследователи стремятся разобраться во всех его нюансах, изучить свойства и строение каждой молекулы. Одна из них — это белок титин. В мышечном волокне он играет роль биологической «пружины», которая соединяет его подвижные части вместе и удерживает волокно от чрезмерного растяжения. Хоть титин и не играет роль главного «мотора» в сокращении мышцы, он, тем не менее, очень важен, поскольку обеспечивает ее эластичность и возврат в исходное состояние при расслаблении. «Поломки» этой молекулы или кодирующего ее гена могут быть причиной серьезных патологий, в частности кардиомиопатии. По этой причине биологам нужно во всех деталях понимать механику этой молекулы, причем не только in vivo, но и изолированной молекулы самой по себе. Таким образом, титин становится объектом изучения для атомной физики, как теоретической, так и экспериментальной.
Назвав титин биологической «пружиной», нужно тут же сделать важное уточнение. Несмотря на то что эта молекула играет роль пружины, ведет себя она совсем не так, как мы бы ожидали от обычной металлической пружинки. Обычная пружина обладает жестко заданной конструкцией, все ее части неподвижны, они не живут своей жизнью и не дергаются туда-сюда. Молекула титина, как и всякая белковая молекула при нормальной температуре, вовсе не неподвижна, а постоянно колеблется: то там, то здесь чуть-чуть распаковывается и снова упаковывается, — в общем, она прощупывает доступное ей пространство конфигурационных состояний (рис. 2). Такое «беспокойство» — неотъемлемая часть существования белковой молекулы, без этого она бы никогда толком и не упаковалась. Но это означает, что для растяжения молекулы требуется преодолевать не только внутреннюю механическую упругость, как у обычной пружины, но и вот это «желание постоянно изменяться». В статистической физике это всё записывается в виде дополнительной энтропийной силы, которая действует наряду с силами механической упругости; поэтому титин справедливее называть «энтропийной пружиной».

Рис. 2. В отличие от обычной механической пружины, в «энтропийной пружине», каковой является титин, появляется дополнительная энтропийная сила упругости, связанная с постоянным «исследованием» этой молекулой разнообразных конфигураций
Главный вопрос в исследовании механики титина — как именно эта молекула растягивается под нагрузкой и как она сворачивается, когда нагрузка исчезает. Исследователям нужно понимать эту механику в мельчайших деталях. Как зависит удлинение молекулы от приложенной силы? Какие участки молекулы расплетаются и на каком этапе? Какие именно связи между какими аминокислотами рвутся при какой нагрузке? Всё это можно изучать экспериментально, буквально взяв молекулу за два конца и растягивая её, можно теоретически, а можно и чисто вычислительно, с помощью моделирования методами молекулярной динамики. Кстати, стоит напомнить, что именно за молекулярное моделирование биологических важных комплексов была присуждена Нобелевская премия по химии за 2013 год.
Разумеется, при этом нужно убедиться, что всё друг с другом сходится: результаты моделирования согласуются с экспериментальными данными, а теоретические модели правильно схватывают все найденные зависимости. И вот тут, оказывается, имеется одна большая проблема — до сих пор не удавалось напрямую сравнить экспериментальные данные по титину с результатами моделирования. Скорости растяжения молекулы, доступные этим двум методам, различались на порядки: в эксперименте молекулы растягивались слишком медленно, а вычислительные ресурсы просто не позволяли смоделировать поведение молекулы так надолго. Хотя эксперимент и моделирование приводили к разным результатам, было неясно, является ли это расхождение серьезным или же просто отвечает двум разным режимам растяжения.
В последнем выпуске журнала Science была опубликована статья, которая единым махом устраняет эту пропасть. В ней описывается усовершенствованная методика, которая позволяет резко увеличить скорость растяжения молекулы в эксперименте и впервые сравнить результаты измерений параметров титина с моделированием. Кроме того, она позволила увидеть тонкие детали этого процесса и, между прочим, вскрыла неточность некоторых теоретических оценок.
Структура и исследования титина
Условно говоря, титин представляет собой этакие молекулярные «бусы». В нем имеется несколько сот крепких компактных модулей иммуноглобулинового типа (Ig-домены), а также специальный легко расплетающийся участок. Эта структура придает молекуле «мягкую» упругость при небольших воздействиях, «жесткую» — при умеренно больших, но одновременно с этим она предохраняет молекулу от разрыва в критических ситуациях.
При обычных физиологических нагрузках концы молекулы растягиваются с силой в несколько пиконьютонов (пН). При этом Ig-домены прочно держат свою форму, а растягивается именно мягкий участок, что позволяет удлинить молекулу до некоторого предела. За этим пределом молекула всё равно не рвется и может растягиваться дальше, но режим упругости здесь меняется. При усилении нагрузки она сначала тянется неохотно, но выше порога силы в 100–200 пН скачкообразно удлиняется примерно на 25 нм. В этот момент распрямляется отдельный Ig-домен. Если растягивающая сила от этого не ослабла, титин снова тянется сначала неохотно, а потом удлиняется еще на 25 нм, и так далее. Шаг за шагом молекула «поддается» слишком большому воздействию, которое она не может удержать, в надежде, что после некоторого значительного удлинения растягивающая сила ослабнет. Подчеркнем, что все эти процессы обратимы: как только воздействие снимается, титин спокойно укладывается в свою естественную (нативную) структуру.
Для того чтобы это всё изучить экспериментально, причем так, чтобы не было разнобоя в экспериментальных условиях, исследователи договорились проводить опыты на «укороченной версии» этой молекулы, состоящей из восьми Ig-доменов, без участка «мягкой» упругости. С одного конца эта молекула прикреплена к устройству, которое тянет ее с определенной скоростью. С другого конца ее держит игла атомно-силового микроскопа, которая находится на краю миниатюрного упругого подвеса — кантилевера. Под действием слабых сил кантилевер чуть-чуть изгибается, этот изгиб удается зарегистрировать, и тем самым можно измерить действующую на него силу. Исследователи запускают механическое устройство, которое медленно, но неумолимо удлиняет молекулу, расплетая ее. При этом снимают показания с атомного силового микроскопа, и в результате получается профиль силы в зависимости от удлинения (рис. 3).

Рис. 3. Эксперименты по растяжению «укороченной версии» титина из восьми Ig-доменов и их типичный результат — кривая силы в зависимости от растяжения молекулы. Изображение из статьи Wolfgang A. Linke et al. 2002. PEVK Domain of Titin: An Entropic Spring with Actin-Binding Properties
Эта кривая имеет характерную пилообразную форму. Каждый зубец отвечает нарастанию силы при растяжении молекулы, а после того как расплетается один из Ig-доменов, механическое напряжение резко падает, и сила «прыгает» вниз. Так происходит восемь раз, после чего вырастает последний высокий зубец, который уже не скомпенсировать никаким расплетанием, и затем молекула отрывается от кантилевера. Кроме этих очевидных особенностей, кривая содержит и дополнительную информацию: это, например, высота и профиль зубцов, резкость падения силы после расплетания очередного Ig-домена, одинаковость зубцов, а также зависимость всего этого от скорости растяжения молекулы. И оказывается, из этих мелких характеристик можно извлечь немало информации о процессе расплетания титина.
Совпадают ли данные этих экспериментов с результатами моделирования? На рис. 4 приведено сравнение (по состоянию на 2009 год) для одной конкретной характеристики явления — критической силы в зависимости от скорости растяжения. Видно, что критическая сила в эксперименте и в моделировании отличается в несколько раз. Однако эти значения получены при сильно разных скоростях растяжения! Типичные скорости удлинения в эксперименте не превышали нескольких микрон в секунду, и при такой скорости молекуле требуется несколько миллисекунд для распаковки одного Ig-домена. Это огромное время по молекулярным масштабам; достаточно сказать, что для честного расчета динамики молекул шаг по времени должен быть порядка 1 фемтосекунды (10−15 с). Миллион шагов — это всего лишь 1 наносекунда; и то, до таких времен моделирование дотянулось лишь 10 лет назад. Три года назад суперкомпьютер смог просчитать целую миллисекунду — правда, только для небольшой молекулы. А что касается моделирования титина, то тут типичные скорости растяжения составляли сантиметры и даже метры в секунду — иначе компьютер не успел бы промоделировать ничего интересного. Фактически, моделировалось не растяжение молекулы, а, скорее, рывок. Самое медленное удлинение, которое физики смогли пока промоделировать, отвечало скорости около 3 мм в секунду, что всё еще в тысячу раз превосходило возможности эксперимента.
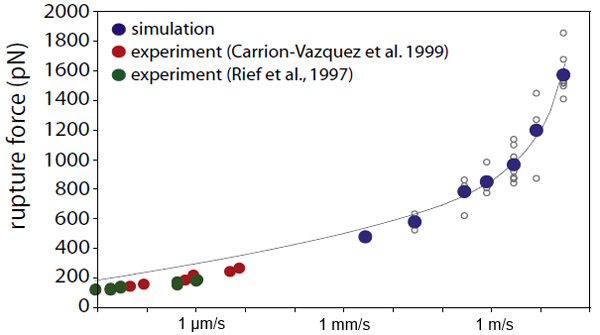
Рис. 4. Сравнение экспериментальных данных и результатов моделирования по состоянию на 2009 год на примере критической силы в зависимости от скорости удлинения. Видно, что область скоростей, доступная эксперименту (красные и зеленые точки), отличается от скоростей, доступных в моделировании (синие точки), почти в тысячу раз. Изображение из статьи Eric H. Lee et al., 2009. Discovery Through the Computational Microscope
У читателя здесь могут возникнуть два вопроса. Во-первых, почему вообще есть разница, с какой скоростью растягивать молекулу? Ведь нам, по большому счету, хочется узнать лишь, какие там действуют силы да что в каком порядке расплетается. Причина опять-таки в том, что титин — это «энтропийная пружина». Её упругость возникает не только из-за роста потенциальной энергии при растяжении, но и за счет того, что молекула постоянно меняется, постоянно «прощупывает» доступные ей пространственные конфигурации. Если молекулу растягивать медленно, то она успеет под нагрузкой прощупать все близкие конфигурации и «найти» самый оптимальный путь к распаковке Ig-домена. Но если скорость резко увеличить, то молекула просто не успеет за выделенное время найти оптимальный путь. В результате при растяжении рывком «энтропийность» пружины уже не важна; процесс распаковки станет более грубым, механическим, непохожим на медленное удлинение. Поэтому критическая сила и возрастает.
Во-вторых, может удивить, что эксперименты долго не могли ускорить растяжение больше чем до нескольких микрон в секунду. Конечно, причина не в самом растяжении, а в точности измерений. Под действием переменной силы кантилевер дрожит, и пока эта дрожь не прекратилась, он не может показывать правильные данные. При больших скоростях движения эта тряска кантилевера замазывала все реальные силы, которые слишком быстро менялись со временем. Поэтому быстро растягивать молекулу было просто бессмысленно — никаких данных получить не удалось бы.
Новые результаты
Эта сложность, вкупе с некоторыми сопутствующими трудностями, и была преодолена в новой статье в Science. Ее авторы использовали экстремально короткий кантилевер, длиной всего в несколько микрон и с периодом свободных колебания меньше микросекунды. Казалось бы, совершенно незначительное усовершенствование! Но в результате установка заработала на три порядка быстрее, чем классический атомно-силовой микроскоп, и кроме того, ей открылся огромный динамический диапазон скоростей — от 0,01 до 3870 мкм/с. Благодаря этому исследователям удалось полностью перекрыть весь недоступный ранее интервал и впервые сопоставить друг с другом результаты эксперимента и моделирования. Кроме того, благодаря высокому временному разрешению они смогли аккуратно изучить те явления и измерить те величины, которые ранее были недоступны прямому наблюдению.
Итак, прежде всего исследователи убедились, что при очень низких скоростях их измерения согласуются с данными прошлых экспериментов, а при высоких скоростях — с результатами моделирования (рис. 5). Таким образом, они впервые перекинули мостик через пропасть, разделявшую эти два метода исследования титина.

Рис. 5. Слева: профиль сил в зависимости от удлинения при разных скоростях растяжения. Высота зубцов отвечает критической силе при данной скорости. Справа: зависимость критической силы от скорости; черные точки — новые результаты, квадратики — результаты прошлых экспериментов, треугольники — результаты моделирования. Изображение из обсуждаемой статьи в Science
Во-вторых, было впервые показано, что рост критической силы на этом графике не линейный, а круто загибается вверх. По-видимому, это является указанием на то, что при скоростях выше 1 мм/с меняется режим расплетания молекулы. Такое поведение предполагалось и ранее, но только сейчас оно было наглядно продемонстрировано.

Рис. 6. Профиль одного зубца при медленном растяжении. Стрелкой указан тот момент, когда профиль «срывается» на слегка сдвинутую кривую. Изображение из обсуждаемой статьи в Science
В-третьих, видно, что экстраполяция данных в область еще больших скоростей, порядка несколько сантиметров в секунду и выше, предсказывает намного большие значения силы, чем те, что получаются в моделировании. Является ли это расхождение чем-то серьезным, пока сказать трудно. Если оно подтвердится в будущем, то это может означать, что в моделировании сделаны некоторые не вполне справедливые предположения о силах, действующих между частями молекулы. Таким образом, это сравнение поможет улучшить надежность вычислительных результатов.
В-четвертых, благодаря высокому временному разрешению удалось измерить профиль каждого зубца с недостижимой ранее точностью. В этих измерениях стала четко видна одна особенность, на которую предыдущие эксперименты только слегка намекали: при превышении некоторого промежуточного порога силы зубец растет чуть медленнее, чем поначалу (стрелка на рис. 6). Более аккуратные измерения показывают, что зубец чуть-чуть сдвигается вбок (цветные кривые на рис. 6). Такой переход означает, что в этот момент происходит небольшое ослабление упругости, и молекула чуть-чуть удлиняется, примерно на 0,9 нм (оценки предыдущих экспериментов давали удлинение всего на 0,3 нм). Подчеркнем — это происходит до полного расплетания Ig-домена, но явно как-то с ним связано.
И действительно, результаты моделирования предсказывают, что Ig-домен расплетается не мгновенно, а вначале переходит в промежуточное состояние. В частности, самый первый этап — это разрыв трех водородных связей между β-тяжами, помеченными буквами A и B на рис. 7. Именно в этот момент происходит предварительное удлинение молекулы как раз на 1 нм (что прекрасно согласуется с новыми данными), а уж потом, при еще больших нагрузках, начинают расплетаться и другие части Ig-модуля.

Рис. 7. Три начальных этапа расплетания Ig-домена в титине. Слева: нативная структура, в центре: промежуточное состояние с тремя разорванными связями, справа: последующие этапы расплетания молекулы. Изображение с сайта www.ks.uiuc.edu
В-пятых, хоть это и не показано на графиках, но авторам удалось извлечь из своих данных разнообразные термодинамические характеристики этого белка. Они определили энергию возбуждения промежуточного состояния и выяснили, что она вполне согласуется с разрывом трех водородных связей между участками A и B. Они также выяснили, при какой нагрузке активируется это промежуточное состояние, оценили, сколько раз в секунду молекула перескакивает из нативного состояния в промежуточное и обратно, а также как быстро молекула возвращается в нативное состояние после снятия нагрузки. Некоторые из этих величин сильно отличались от прежних оценок.
Авторы заканчивают свою статью справедливым замечанием, что область применения их установки не ограничивается одним лишь титином. На ней можно будет изучать динамику других биологически важных молекул, принимающих участие в тех или иных механических процессах внутри клетки. Тот факт, что эти измерения могут теперь дотянуться до результатов моделирования, позволит уточнить программы моделирования и улучшить общее понимание молекулярных биомеханических процессов.
Источник: F. Rico et al. High-Speed Force Spectroscopy Unfolds Titin at the Velocity of Molecular Dynamics Simulations // Science. 2013. V. 342. P. 741.
См. также:
1) Торжество компьютерных методов: предсказание строения белков, «Биомолекула», 26.03.2008.
2) Помогать науке можно играя, «Элементы», 01.09.2010.
-
А зачем такие сложные термины как "энтропийные силы"? Есть же понятие вязкости и силы вязкого трения. Что сила сопротивления возрастает со скоростью и имеет довольно сложную зависимость - это давно известно.
-
Не-не, это не взякость и не сила трения. Это дополнительная сила, которая появляется у пружинкм потому, что при разной длине у нее разная энтропия.
Вот смотрите, классический пример, одна из первых задач в курсе статистической физики. Представьте себе этакую складную линейку, состоящую из отдельных жестких звеньев, соединенных шарнирами, нечто типа
\/\/\/\/\/\/\/\/
Пусть шарниры могут проворачиваться свободно, т.е. никакой силы упругости нет вообще. И пусть для простоты звенья совсем не мешают друг другу. Вопрос: какую силу нужно приложить, чтоды удлинить эту линейку?
В обычном механическом рассмотрении мы записываем пеотенциальную энергию упругости E. Но она тут равна нулю для любого растяжения, так что никакого сопротивления эта линейка не оказывает и сколько угодно малая сила будет ее удлинять.
А в термодинамике, для системы при фиксированной температуре, нужно смотреть не на энергию, а на свободную энергию F = E - TS, где S — энтропия. Система стремится к понижению F, так что даже если E=0, остается все равно некая энергия, минимум которой достигается при максимальной энтропии. А максимум энтропии достигается, когда вся линейка сжалась в компактный клубок. А если ее существенно растянуть, то там энтропия намного меньше, и она будет понижаться еще при дальнейшем растяжении. Т.е. F увеличивается с растяжением — производная и является энтропийной силой.
Этот пример должен быть во всех учебниках/задачниках по статфизике.
Вот еще пара ссылок (на английском, к сожалению):
http://johncarlosbaez.wordpress.com/2012/02/01/entropic-forces/
http://butler.cc.tut.fi/~vattula2/teaching-bf/LECTURE06-Nelson-Chapter07-2012.pdf — куча вариантом энтропийной силы -
Дорогой афтар, таки уж поищите ссылки получше, раз уж взялись за блаародное дело популяризации науки. Первая вообще принадлежит не физику, а топологу (поправьте, если я чего-то о нём неправильно знаю), известному больше игривостью стиля и желанием выглядеть классиком науки, чем конкретными математическими достижениями (я работаю, если брать достаточно широко, в той же области, так что кое-что знаю - но поправки, повторяю, приму есичё). И по-русски, плиз - а если не найдёте, так сами напишите доходчивую статью "Энтропийные силы". Или вы думали, что популяризация - это такая синекурица сплошная?
PS. Ваше краткое объяснение выше, однако, неплохое. Желающие могут в него внимательно вчитаться и понять суть дела.-
> Дорогой афтар, таки уж поищите ссылки получше, раз уж взялись за блаародное дело популяризации науки.
Давайте я сделаю выжимку из ваших слов:
*) вы не высказали претензию (пока что?) ко всей совокупности моих новостей в целом,
*) вы не высказали претензию к этой новости самой по себе,
*) вы не высказали претензию к моему ответу другому участнику, более того, вы его даже рекомендуете почитать,
*) вы не высказали претензию к истинности той информации, которая по ссылкам,
*) вам лишь не понравилось, что по первой Баез (то, что вам не нравится его стиль, это ваше личное отношение, а то, что он занимается давно и активно не только фундаментальной математикой, вы должны вроде бы понимать), а также что обе на английском. Т.е. единственная претензия к тому, что сущестувуют ссылки получше, но я их не указал.
И на основании этого вы мне даете глобальные рекомендации насчет того, что я должен делать и как я должен популяризировать физику. Комментарии не требуются.-
Ещё раз заглянул на эту страничку. Игорь Иванов, я же вообще не высказывал претензий, вы уж очень эмоционально реагируете. Я всего лишь высказал доброе пожелание, ну немного в тоне мехматской хуцпы (тех лет, когда я там учился) - но это чтобы популяризаторов в тонусе держать :D Я зарабатываю на жизнь преподаванием, так что практически машинально думаю о других читателях (а сам я вполне себе математический физик, и на языках разных понимаю, вопрос не во мне, и зря здесь ниже переходили на личности :D ).
Давайте, работайте, всё будет хорошо!
-
-
-
-
-
-
Очень жаль, тут я должен признать что при отличном университетском математическом образовании и отличном школьном знании физики, физику университетского уровня я понимаю через пень-колоду.
Правильно ли я понимаю, что энтропийные силы отражают тот заём энергии, который можно получить у внешней среды за счет околотепловых процессов? К примеру, вода с мокрой тряпки испаряется с расходованием тепловой энергии внешней среды. Т.е. эта сила - следствие того, что у нас эксперимент в незамкнутой системе?
По вашим ссылкам я почитал, спасибо, иначе ничего бы не понял. Но недостаток ваших ссылок в том, что остаётся подвешенным в воздухе вопрос "ну и причем тут скорость процесса, она не входит в уравнение состояния и в энтропию тоже". Почему я заговорил о силе трения. Сила трения меняет знак как только меняет знак скорость. Сила натяжения пружины - нет. Точно также не пропадает давление в газовом поршне, если его перестать двигать - давление просто остаётся постоянным (возможно, если сжатие было адиабатическим, и поршень нагрелся, то давление далее будет плавно падать, но упадёт не очень сильно, и это детали). Т.е. вопрос в том, что если натянуть волокно, так что оно разматывается с очень большой скоростью и мгновенно уменьшить силу в 2 раза. Что будет? Я вижу 2 варианта: а) пружина качнётся в обратном направлении, потому что тут есть вполне определённые силы, в первом приближении зависящие от формы, т.е. пружина готова вернуть накопленную энергию б) пружина продолжит процесс растяжения, но скорость растяжения будет заметно ниже, как и свойственно движению в условиях вязкого трения - энергия трения ушла в тепло и не вернётся.-
У Фейнмана в лекциях есть глава - почему пружинит резина. Там самое наглядное объяснение которое я встречал.
-
Так у него и ответ там есть. При растяжении резинки энтропия уменьшается и она нагревается. Когда резинку нагревают, она сжимается и приподнимает грузик, подвешенный на резинке. Очень наглядно.
При быстром растяжении молекула просто не успевает остыть и сопротивляется сильнее.
Про энтропию можно здесь почитать: http://modcos.com/articles.php?id=61
-
-
Тут у читателя может сложиться неверное представление. Речь идет о глобулярных белках. Вот это "то там, то здесь" это их поверхность, а ядро у них как раз на удивление жесткое. Часто, для большей жесткости еще и прошитое дополнительными ковалентными связями.
Здесь бы хорошо либо приводить полную картинку, либо вообще об этом не говорить.
-
Про энтропийность пружины все-таки надо сказать, это очень полезно для объяснения, почему от скорости растяжения может зависеть упругость. Но в тонкости того, какие именно прощупываются конфигурационные состояния (т.е. где именно там происходит фолдинг/дефолдинг), по-моему, пускаться уже не требуется. У меня и так в новостях часто перегруз информацией, мне приходится удалять куски, которые хоть и интересные, но уводят немножко в сторону.
-
Про энтропийность обязательно надо. Но может быть как-то изменить фразу чтобы не сложилось впечатления что белок это некая полурасплавленная капля. Мне так показалось из текста.
-
А по мне как раз очень правильно сказать, что белок - это полурасплавленная капля. Т.к. он вне воды наверняка имеет совершенно другие свойства.
-
Это не мнение. Этот вопрос хорошо изучен.
Ядро нормального белка это максимально твердый каркас. На нем расположены вещи обеспечивающие функции. Вот они могут быть любыми.
Конечно и ядро может быть подвижно. Но это не общий случай, а когда это требуется для какого-то механизма. (Кстати, не знаю как в титине, поскольку его функция как раз в многократном сворачивании) Фантастическое устройство на самом деле. С одной стороны он не далеко от температуры плавления, с другой, он должен обеспечивать жесткий каркас.
-
-
-
Да и теоретики этим занимаются очень давно: во-первых, энтропийный вклад в упругость полимерной цепи описал не то Флори в 1950-е, не то Эдвардс с Лифшицем в 1960-е. Прекрасно согласуется с экспериментом. Во-вторых, именно задача экспериментального исследования случайно рвущихся связей кантилевером АФМа привела к расцвету флуктуационных теорем двадцать лет назад.
-
Хорошо, когда появляется специалист. Правда, у специалистов часто встречаются шапкозакидательсткие интонации :) но это терпимо.
Работа, конечно, про эксперимент, моделирование и тем более теорию не трогаем. (Хотя насчет симуляций таких молекул вы, по-моему, тоже перегибаете палку, на масштабе миллисекунд это еще не сделано даже на Антоне.)
Если вы говорите, что аналогичные методы давно используются в других группах, то объясните, почему ж они их к титину не применили? Ведь причитание об огромном разрыве между моделированием и экспериментами по растягиванию повторяется из статьи в статью. А ссылки на данные AFM и оптических ловушек при этом почему-то ограничиваются только 1999-2000 годами.
Или вы имеете в виду, что метод пусть и новый, но информация о свойствах титина, которую они а статье сообщают, была известна и раньше? Ну, тут я спорить не буду, революционного ничего не обнаружено, но всё-таки хорошо, когда это подтверждается и уточняется прямым экспериментом в тех же условиях, где есть результаты моделирования.
Для меня здесь интересно следующе.
В технике есть метод увеличения порога чувствительности АЦП путем подключения к входу АЦП источника шума. При этом, после фильтрации сигнала можно получит разрешение значительно выше порога дискретизации АЦП. Если этого не делать, то сигнал бы застревал на определенных ступеньках, равных порогу дискретизации АЦП.
Похоже, что природа использует этот же принцип для построения оптимальных свернутых конфигурации полипептидных цепочек (белков), при наличии шума (теплового движения молекул). При этом, в процессе сворачивания, существует возможность выбора между множеством различных вариантов, в том числе отличающихся друг от друга с энергетической точки зрения на очень незначительную величину. В противном случае фолдинг белка был бы невозможен, т.к. полипептидная цепочка при сворачивании могла бы застревать в одном из неоптимальных вариантов.
Смысл в том, что в такой системе на процесс фолдинга могут влиять очень слабые силы, относящиеся, например, к сверхтонкому взаимодействию (возможно и меньше), и искажающие симметрию электронных оболочек на очень незначительную величину - поскольку порога чувствительности при выборе двух близких вариантов практически нет.
-
По смыслу Вы сейчас написали про стохастический резонанс. В случае динамики молекул, насколько мне известно, данное понятие не имеет смысла. Молекуле не нужно "знать" конкретный переход между двумя очень близкими по энергии конформационними состояниями из огромного числа возможных. Это нужно Вам для усиления чувствительности к конкретному сигналу. В этом и заключается смысловая разница между эволюцией собственно системы и актом измерения этой эволюции.
Расплетите молекулу белка и заморозьте - фолдинг станет невозможен. Нагрейте - конформация восстановится. В чем Ваш вопрос заключается?-
Согласно мысли, которую высказал Игорь Иванов, молекула при движении постоянно «прощупывает» доступные пространственные конфигурации. При этом части молекулы не фиксированы и немого колебаются (иначе как можно объяснить физику этого процесса?).
Фазовое пространство движения частей молекулы можно сравнить с неровным рельефом. Если шума нет, то конфигурация молекулы при своем движении застревает в одной из ближайших потенциальных ям. Возможно, случайным образом. Если есть шум, то рельеф как - бы сглаживается. Части молекулы при движении постоянно «измеряют» потенциал не конкретных ближайших потенциальных ям, а некоторый усредненный потенциал вокруг себя. Возможно, на очень большую глубину (при высокой степени усреднения) и скатываются в направлении максимального уклона. Т.е. дискретизации при измерении потенциала молекулой исчезает.
Если вход АЦП, вместе с сигналом, подать белый шум, на выходе АЦП появляется информация о значении измеряемой величины с большим разрешением, чем величина дискретизации АЦП. Точно также измеряет потенциал молекула. При наличии шума у молекулы появляется возможность «видеть» окружающее пространство в усредненном виде с очень высоким разрешением.
Следствием этого являтся то, что усредненный потенциал вокруг молекулы или ее части может быть очень небольшой величины, значительно ниже локальных потенциалов (т.к. микронеровности сглаживаются). Рельеф фазового пространства может допускать развилку, направления которой могут очень незначительно отличатся друг от друга, или вообще может быть плоская поверхность одного уровня. При этом на исход движения молекулы могут влиять очень незначительные силы, например магнитные моменты атомных ядер или мультипольные моменты, нарушающие симметрию электронных оболочек.
tetrapack: «Расплетите молекулу белка и заморозьте - фолдинг станет невозможен.»
Это так. Молекула белка «замерзнет». Ее конфигурация скатится в одну из микронеровностей рельефа фазового пространства.
tetrapack: «Нагрейте - конформация восстановится.»
Это так. В этом случае микронеровности сгладятся, и будет движение.
tetrapack: В чем Ваш вопрос заключается?»
Вообще говоря, я не задавал никакого вопроса. Я просто хотел поговорить на интерсующуую меня тему. (Поскольку здесь она может считаться, по моему мнению, умеренным оффтопиком, детализирующем физику одного из механизмов живой природы.)-
Мне показалось, что вы задали вопрос, видимо из-за фразы "Для меня интересно следующее" Теперь понятно, что вопроса не было.
В статье имелось в виду не то, что молекула "прощупывает" или "не прощупывает" возможные конформационные состояния, а "успевает ли она прощупать" все доступные состояния в зависимости от скорости ее растяжения. Т.е. равновесное ли оно, или нет. Здесь больше подходит аналогия не со стохастическим резонансом, а с термодинамическими процессами. Равновесный термодинамический процесс идет с совершением максимально возможной работы, неравновесный - нет. Говоря иначе, при резком растяжении "энтропийная упругость" будет меньше, чем при плавном, несмотря на то, что в обоих случаях убыль энтропии (начальное состояние - конечное) будет, в общем-то, одинакова. Сила упругости будет совершать меньшую работу в первом случае, чем во втором.-
Я хотел сказать немного другое. Я рассматривал ситуацию в общем виде немного с другой стороны. Но если говорить о титине, то с рассматриваемой мною точки зрения можно написать следующее.
В случае если растяжение титина происходит с высокой скоростью, молекула и ее части в каждой новой конфигурации за короткий отрезок времени могут совершить небольшое количество колебаний. В результате окружающий части молекулы потенциал усредняется слабо и она плохо «видит» внешнее окружение. Траектория движения частей молекулы в фазовом пространстве становится сложной. При этом части молекулы часто попадают в потенциальные ямы, чтобы выбраться из которых необходимы усилия.
Это предположение хорошо поддерживается графиками в обсуждаемой статье.
-
-
-
Игорь, может быть, все-таки "объектом изучения для квантовой химии (молекулярной динамики, полуэмпирических методов и т.д)".
-
Это все хорошо, но в самом начале новости я обычно стараюсь говорить самые простые слова, чтоб их успели схватить люди, для которых все эти комбинации слов нечто новое. (А мысль о том, что маленькие штучки внутри клетки — это объект изучения не только биологии, он и химии, физики и т.д., для многих нетривиален.)
Ну и кроме того, я имел в виду, прежде всего, эксперименты, так что сразу уводить все в расчетную сторону не стоит, как мне кажется.
Последние новости

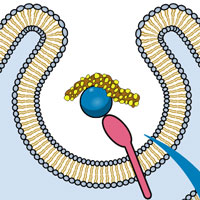












Рис. 1. Схематичное изображение молекулярного устройства поперечно-полосатой мышцы. В этом упорядоченном разнообразии молекул присутствует и белок титин (темно-синие ниточки), который удерживает всю эту конструкцию вместе и препятствует излишнему растяжению мышечного волокна. Изображение из статьи John C. Sparrow & Frieder Schöck. 2009. The initial steps of myofibril assembly: integrins pave the way