Критическая температура сверхпроводника может быть увеличена магнитным полем

Рис. 1. Усиление сверхпроводимости параллельным магнитным полем в ультратонкой аморфной пленке свинца. Абсолютное (шкала слева) и относительное (шкала справа) увеличение критической температуры T_c по отношению к T_c0 = 3,814 K для пленки в отсутствие магнитного поля. Толщина пленки 21,1 Å. По оси абсцисс отложена индукция магнитного поля в теслах. Рисунок из обсуждаемой статьи в Nature Physics

Сверхпроводимость — это квантовое состояние вещества, которое, помимо внешних признаков — отсутствия сопротивления и абсолютной невосприимчивости к магнитному полю, — характеризуется формированием синхронизированных между собой пар из электронов проводимости. В силу особенностей строения и характеристик электронных пар магнитное поле с индукцией выше определенного уровня уменьшает критическую температуру сверхпроводника, то есть температуру, ниже которой в нём реализуется явление сверхпроводимости. Коллектив американских ученых, проведя эксперименты с ультратонкими (порядка 10^–9 м) аморфными пленками свинца, обнаружил, что сильное магнитное поле, наоборот, повышает их критическую температуру. Полученный результат противоречит общепринятой теории сверхпроводимости.

Причиной возникновения сверхпроводимости, то есть появления у вещества бесконечно большой проводимости и идеального диамагнетизма (выталкивания внешнего магнитного поля), является формирование в нём пар из электронов проводимости, ведущих себя затем синхронизированным образом. Такое единство позволяет электронам без трения протекать через кристаллическую решетку материала и слаженно «отражать атаки» силовых линий магнитного поля.

Согласно общепринятой микроскопической теории сверхпроводимости (известной еще как теория Бардина—Купера—Шриффера или, сокращенно, БКШ), формирование электронных пар происходит, когда температура вещества становится меньше определенной величины, индивидуальной для данного материала, — критической температуры T_c. При температуре ниже T_c электроны, посредством обмена фононами, притягиваются друг к другу и образуют пару, часто называемую куперовской по фамилии американского физика-теоретика Леона Купера, предсказавшего это явление. Сейчас такое притяжение известно как электрон-фононное взаимодействие; при температуре ниже критической оно становится сильнее, чем кулоновское отталкивание этих одноименно заряженных частиц.

Здесь важно отметить, что в теории БКШ образование куперовских пар возможно лишь из электронов с противоположно направленными импульсами и спинами. Напротив, в так называемых «необычных» сверхпроводниках, сверхпроводящие свойства которых не объясняются теорией БКШ, направления спинов электронов в куперовских парах могут совпадать.

Определение сверхпроводимости позволяет понять, как ее можно разрушить. Первый способ — нагреть сверхпроводник до температуры выше критической. Второй — усиливать магнитное поле настолько, чтобы сверхпроводящий материал уже не мог отталкивать силовые линии этого поля. На микроскопическом уровне разрушение куперовских пар теплом объясняется понижением энергии связи электронов в куперовской паре. В случае усиления магнитного поля разрушение пар электронов объясняется двумя эффектами — парамагнитным и орбитальным. Парамагнитный эффект заключается в стремлении магнитного поля выстроить спины электронов в направлении своих силовых линий. Поскольку спины в куперовской паре, как уже было сказано, имеют антипараллельное направление, то когда сильное магнитное поле выпрямляет «неправильную» ориентацию одного из электронов пары, ей уже с точки зрения энергии невыгодно продолжать свое существование (действует принцип Паули). Орбитальный эффект состоит в том, что, поскольку импульсы электронов в паре направлены противоположно, на каждый электрон будет действовать разнонаправленная сила Лоренца, которая будет растягивать частицы в куперовской паре подобно нитке, концы которой тянут в разные стороны.

Из всего сказанного можно сделать следующий вывод: в теории БКШ нет механизма, который делал бы куперовские пары прочнее в магнитном поле, повышая тем самым критическую температуру сверхпроводника. Справедливости ради, правда, стоит заметить, что существуют соединения на основе урана, которые в сильных магнитных полях восстанавливают сверхпроводимость, утраченную ранее в более слабом поле (см. Открыта экзотическая сверхпроводимость в сильном магнитном поле, «Элементы», 30.08.2005). Однако эти сверхпроводники относятся к уже упомянутой категории «необычных», для которых теория БКШ неприменима. Каким образом магнитное поле стимулирует в этих веществах возрождение сверхпроводимости, для ученых пока неясно.

В связи с этим опубликованные в журнале Nature Physics результаты экспериментов группы американских ученых кажутся удивительными и весьма неожиданными. Авторы этой работы сообщают о росте критической температуры ультратонких (толщина порядка 10 Å, 1 Å = 10^–10 м) пленок свинца с увеличением индукции магнитного поля, силовые линии которого ориентированы параллельно поверхности исследуемых образцов. Неординарность полученных результатов прежде всего здесь состоит в том, что свинец относится к числу «обычных» сверхпроводников, для которых прекрасно работает теория БКШ. А потому при увеличении индукции магнитного поля критическая температура должна по квадратичному закону уменьшаться.

Для начала несколько слов о методике эксперимента. Во-первых, изучение данного явления проходило в диапазоне индукций магнитного поля от 0 до 8 Тесла (Тл). Во-вторых, изменение ориентации магнитного поля с параллельной пленкам на перпендикулярную приводило к тому, что критическая температура образцов ожидаемо уменьшалась. В-третьих, свинцовые пленки были аморфными. Иными словами, в материале отсутствовала кристаллическая решетка, и расположение атомов носило неупорядоченный характер. Попутно также стоит отметить, что в таких практически двумерных (или, как говорят, квазидвумерных) конфигурациях свинца его критическая температура существенно зависит от толщины и может быть в несколько раз меньше критической температуры для массивных образцов данного вещества, которая составляет около 7,2 К.

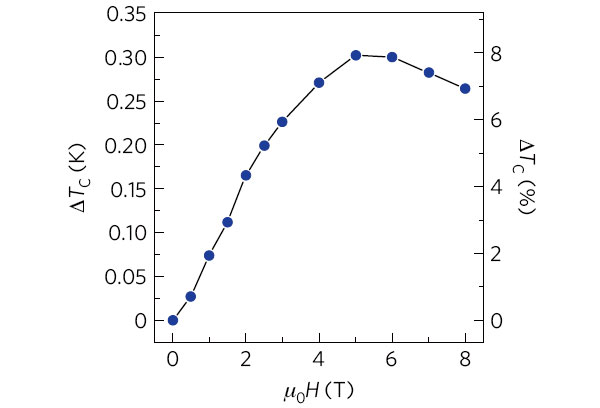
На рис. 1 представлен, пожалуй, основной результат экспериментальных изысканий авторов статьи. На нём приведены данные по приросту ДT_c критической температуры аморфной свинцовой пленки толщиной 21,1 Å в зависимости от прикладываемого к ней параллельного магнитного поля.

Интересно, что данная зависимость носит явно немонотонный характер. Максимальное увеличение T_c наблюдается, когда индукция магнитного поля составляет приблизительно 5 Тл. Чтобы уяснить, насколько велико для сверхпроводящего свинца это значение, скажем, что в массивных образцах, температура которых близка к абсолютному нулю, сверхпроводимость исчезает в полях с индукцией выше всего 0,08 Тл.

На первый взгляд может показаться, что увеличение не такое уж значительное, всего лишь на 8%, или на 302 милликельвина в абсолютных единицах (см. рис. 1), однако здесь важен сам факт присутствия этого роста и то, при каких огромных значениях магнитного поля наблюдаемый эффект реализуется в сверхпроводнике, для которого магнитное поле, как известно, является «врагом».

Далее в своих изысканиях авторы заинтересовались вопросом, как эволюционирует критическая температура квазидвумерных образцов, если менять их толщину. Ответ приведен на рис. 2, где визуализированы экспериментальные данные, показывающие увеличение T_c для набора из восьми пленок разной толщины.

Рис. 2. Зависимость роста ΔT_c критической температуры квазидвумерных аморфных пленок свинца от их толщины (приведена на графике) в параллельном магнитном поле. Для самой тонкой пленки (красные квадраты) критическая температура в отсутствии магнитного поля составляет T_c0 = 0,486 К, для самой толстой (фиолетовые треугольники), которую можно уже интерпретировать как массивный трёхмерный образец, T_c0 = 6,44 К. Рисунок из обсуждаемой статьи в Nature Physics

Как и на графике рисунка 1, данная зависимость также имеет свои особенности. Оказывается, максимальное приращение критической температуры реализуется не для самой тонкой пленки, как вроде бы должно было быть, а для образца с промежуточной толщиной 21,1 Å (данные по этой пленке были приведены на рис. 1). В целом же, практически все зависимости на качественном уровне совпадают: до определенного значения магнитного поля критическая температура растет, потом следует максимум, затем монотонное убывание.

Каковы могут быть причины обнаруженного явления, для авторов публикации пока остается загадкой. Ученые в своей статье выдвинули несколько гипотез, однако аргументы носят эвристический характер и претендовать на окончательное объяснение не могут. К тому же, как замечают исследователи, необходимо более тщательно промерять величину эффекта в зависимости от толщины образцов, наличия в них магнитных примесей и прочих характеристик вещества, которые могут оказать влияние на прирост критической температуры.

Источник: H. Jeffrey Gardner, Ashwani Kumar, Liuqi Yu, Peng Xiong, Maitri P. Warusawithana, LuyangWang, Oskar Vafek, Darrell G. Schlom. Enhancement of superconductivity by a parallel magnetic field in two-dimensional superconductors // Nature Physics. 2011. V. 7. P. 895–900.

Юрий Ерин