Найдена геометрия, в которой сила Казимира становится отталкивающей

Рис. 1. Пример геометрии, в которой эффект Казимира приводит к расталкиванию тел: металлическая частица в форме сфероида «зависает» над центром круглой дырки в металлической пластине. Рисунок из обсуждаемой статьи в Phys. Rev. Lett.

Взаимное притяжение двух металлических тел в вакууме, возникающее на расстояниях менее 1 мкм, называют эффектом Казимира, а силу, с которой тела притягиваются, — силой Казимира. Хотя эффект Казимира известен уже более 60 лет и неоднократно проверялся экспериментально, до сих пор не было ясно, можно ли так подобрать геометрическую конфигурацию двух тел с металлической проводимостью, что между ними будет наблюдаться не притяжение, а отталкивание. Группа физиков-теоретиков из Массачусетского технологического института и Гарвардского университета нашла пример геометрии, в которой два металлических объекта в вакууме испытывают казимировское отталкивание.

Традиционно эффект Казимира объясняют квантовыми флуктуациями электромагнитного поля в вакууме. Согласно принципу неопределенности Гейзенберга, вакуум представляет собой не абсолютную пустоту. В нём постоянно флуктуируют (рождаются и почти сразу исчезают) пары различных частиц и античастиц, среди которых есть и фотоны, то есть кванты — переносчики электромагнитного взаимодействия. Чаще всего эффект Казимира наблюдается в случае притяжения двух параллельных незаряженных металлических пластин. Расчеты показывают, что в пространстве, зажатом между пластинами, число рождающихся фотонов меньше, чем снаружи. Из-за такого дисбаланса в количестве частиц давление, которое оказывают фотоны извне, становится больше давления в зазоре между пластинами, и между пластинами возникает притяжение, которое назвали силой Казимира. В последующих теоретических исследованиях эффекта Казимира обнаружилось, что притягиваться могут не только параллельные пластины, но и тела произвольной геометрической формы. Главное, чтобы они обладали металлической проводимостью.

Через несколько лет после открытия эффекта Казимира советский физик Евгений Лифшиц описал эти квантовые флуктуации и обнаружил, что сила Казимира может возникать не только между металлическими телами с разделяющим их вакуумным промежутком, но и между объектами с произвольными значениями диэлектрической проницаемости. Из такого обобщения эффекта Казимира, впоследствии получившего название «эффект Казимира–Лифшица», следовало, что при определенных соотношениях диэлектрических проницаемостей тел, а также материала, заполняющего зазор, объекты могут не притягиваться, а, наоборот, отталкиваться на любых расстояниях. В начале прошлого года величина этого отталкивания было впервые точно экспериментально измерена (см. Впервые измерена сила отталкивания в эффекте Казимира–Лифшица, «Элементы», 21.01.2009).

Тем не менее до настоящего времени было неизвестно, можно ли подобрать такую геометрию двух тел с металлической проводимостью, разделенных вакуумным промежутком, чтобы вместо казимировского притяжения между ними происходило отталкивание? Иными словами, какую форму должны иметь объекты и как они должны быть расположены, чтобы «чистый» эффект Казимира (не эффект Казимира–Лифшица) приводил к их взаимному отталкиванию без всяких ухищрений с диэлектрическими проницаемостями?

Ответ на этот вопрос смог дать коллектив физиков-теоретиков из Массачусетского технологического института и Гарвардского университета. В журнале Physical Review Letters они опубликовали статью Casimir Repulsion between Metallic Objects in Vacuum (доступную также в Архиве электронных препринтов), в которой описывается пример геометрии с казимировским отталкиванием.

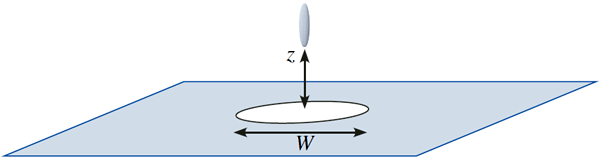
Найденная система состоит из металлической частицы в форме эллипсоида вращения (сфероида), расположенной над центром отверстия в металлической пластине (см. рис. 1). Авторы статьи рассчитали, что взаимодействие частицы с перфорированной пластиной на малых расстояниях приводит к появлению отталкивающей силы Казимира.

Ученые смоделировали упрощенный вариант задачи, рассмотрев поочередно взаимодействие цилиндра (который представляет собой предельный случай сильно сжатого эллипсоида вращения) с перфорированной бесконечно тонкой пластиной и с пластиной конечной толщины. Они исходили из предположения, что цилиндр и пластина изготовлены из «идеального металла» — то есть металла, который совершенно не впускает в себя электромагнитное поле.

Результаты вычислений показаны на рис. 2. Пунктирные красные линии — это зависимость силы Казимира от расстояния между цилиндром и пластиной с отверстием. Параметры геометрии и схема измерения расстояния приведены на вставке.

Рис. 2. Зависимость силы Казимира от расстояния в системе «цилиндр — перфорированная пластина». Положительные значения силы Казимира соответствуют отталкиванию в системе, отрицательные — притяжению. Параметры геометрии приведены на вставке. Расстояние между телами отсчитывается от середины цилиндра до центра отверстия в пластине. Красные пунктирные линии соответствуют расчетам казимировской силы в предположении, что пластина и цилиндр изготовлены из идеального металла (Perfect Metal). Вычисления проведены для пластины с бесконечно малой толщиной (t = 0) и такой же пластины с толщиной 20 нм (t = 20 nm). Сплошная голубая линия — это зависимость казимировской силы для пластины c той же геометрией (толщина 20 нм), но из неидеального металла — золота (Gold). Для сравнения приведены расчеты силы Казимира для идеальной металлической сферы диаметром 60 нм и перфорированной идеальной пластины толщиной 20 нм. Видно, что на любых расстояниях имеет место притяжение. Изображение из обсуждаемой статьи в Phys. Rev. Lett.

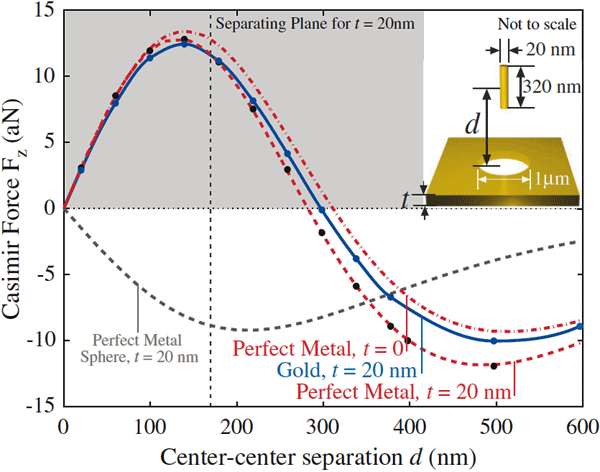
Как видно из хода графиков, существует интервал расстояний (от нуля до примерно 300 нм), когда сила Казимира принимает положительные значения. Это значит, что между цилиндром и пластиной наблюдается отталкивание. Интересно, что полученная учеными зависимость немонотонна, и с увеличением промежутка между объектами сила отталкивания меняется на традиционное для эффекта Казимира притяжение (сила Казимира меньше нуля).

Качественно характер зависимости казимировской силы не изменялся и при рассмотрении реалистичной ситуации с золотым (неидеальный металл) цилиндром и такой же пластиной, имеющей ненулевую толщину (голубая кривая на рис. 2): в определенном интервале расстояний (от 0 до 300 нм) происходит отталкивание, которое затем трансформируется в притяжение.

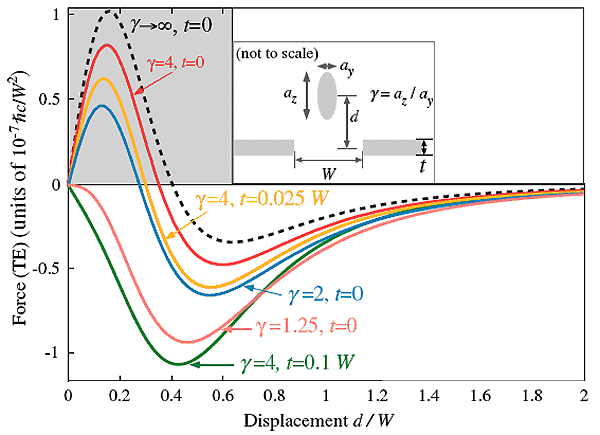
Чтобы определить, как влияет степень сжатия сфероида (отношение его большой полуоси к малой) на поведение казимировской силы, ученые снова рассчитали функцию «сила Казимира — расстояние», зафиксировав размер отверстия в пластине (диаметр отверстия равен 0,002 длины большой полуоси). Выяснилось (рис. 3), что сила Казимира будет отталкивающей, если сжатие сфероида меньше 1,25, а пластина бесконечно тонкая. Для пластины с ненулевой толщиной (в расчетах авторов она составляла 10% от диаметра отверстия) отталкивание имело место только тогда, когда сжатие не превышало 4.

Рис. 3. Влияние формы частицы (сфероида) и толщины перфорированной пластины на зависимость силы Казимира от расстояния. Положительные значения силы Казимира соответствуют отталкиванию, отрицательные — притяжению. Основные геометрические характеристики системы показаны на вставке к графикам; большая полуось a_z = 0,002 W. Величина γ определяет сжатие сфероида. Изображение из обсуждаемой статьи в Phys. Rev. Lett.

Возникает вопрос: как авторы статьи поняли, что именно в такой, далеко не очевидной, геометрии может возникать отталкивание? На исследование подобной системы их натолкнула классическая задача о силе взаимодействия между незаряженной перфорированной плоскостью и диполем, чья ось ориентирована параллельно плоскости. Если вообразить, что диполь — это сфероид, то решение этой задачи формально приводит к тем же результатам, которые наблюдались для такой геометрии на квантовом уровне (в эффекте Казимира): близко расположенный к пластине диполь отталкивается, а на далеких расстояниях — притягивается.

Исходя из такой аналогии, авторы предложили рецепт обнаружения интересных геометрий для расчета пространственного поведения казимировской силы: надо сначала найти систему, которая математически как-то необычно проявляет себя в случае электростатического взаимодействия, а затем аккуратно перенести результаты на эффект Казимира.

Разумеется, не был обойден вниманием и вопрос экспериментального детектирования казимировского отталкивания. Исходя из графика на рис. 2 нетрудно рассчитать, что максимальное расталкивающее давление в изученной геометрии составляет порядка 10^–5 Па, что на один-два порядка меньше существующих экспериментальных методик обнаружения давления в эффекте Казимира. Это, конечно, затрудняет проверку теоретических предсказаний ученых, однако авторы надеются в будущем придумать условия для проверки их предсказания.

Ну и напоследок отметим, что данная система, согласно вычислениям ученых, обладает неустойчивым равновесием, а значит, ни о какой стабильной левитации и, соответственно, применении в каких-либо нанотехнологических процессах говорить не приходится.

Источник: Michael Levin, Alexander P. McCauley, Alejandro W. Rodriguez, M. T. Homer Reid, Steven G. Johnson. Casimir Repulsion between Metallic Objects in Vacuum // Phys. Rev. Lett. 105, 090403 (2010).

См. также:
1) Обнаружена ошибка в расчетах эффекта Казимира для микромеханических устройств, «Элементы», 28.12.2005.
2) Эффект Казимира не может приводить к расталкиванию симметричных тел, «Элементы», 24.10.2006.
3) Впервые измерена сила отталкивания в эффекте Казимира–Лифшица, «Элементы», 21.01.2009.

Юрий Ерин