На основе углеродной нанотрубки создан новый тип масс-спектрометра

Рис. 1. a — изображение углеродной нанотрубки с двойными стенками, полученное просвечивающим электронным микроскопом. Благодаря хорошему разрешению микроскопа возможно с высокой точностью определить массу углеродной нанотрубки (CNT, carbon nanotube) с помощью формулы m_CNT = 2m_Cπ(D_i + D_o)L/A_gr, где m_C — масса атома углерода и A_gr — площадь элементарной ячейки графена. b — устройство атомного сенсора массы (см. пояснения в тексте). Рисунок из обсуждаемой статьи

Ученым из Калифорнийского университета и национальной лаборатории Беркли на основе углеродной нанотрубки удалось создать компактный масс-спектрометр с атомной чувствительностью, который работает при комнатной температуре и не требует необходимой для таких измерений ионизации взвешиваемых частиц.

Традиционно измерение массы атомов или молекул производят с помощью масс-спектрометра. Главный недостаток этого прибора — необходимость превращения объекты взвешивания в ионы (обычно с этой целью используют электроспрей и ионизацию лазерной десорбцией при содействии матрицы, МАЛДИ). В случае, например, определения массы белковых соединений этот процесс крайне нежелателен.

Современный уровень нанотехнологий позволяет избежать таких «варварских» методов. Несколько лет назад было предложено использовать в качестве основного механизма атомных весов наномеханические резонаторы. Суть этого способа, не требующего ионизации частиц, состоит в следующем. У каждого резонатора, не только наномеханического, существует своя частота, определяемая его массой. Когда резонатор начинает адсорбировать атомы или молекулы, то изменение его массы вызывает изменение этой частоты. В общем случае соотношение между изменением массы резонатора и сдвигом его частоты определяется геометрией резонатора и расположением адсорбированных частиц. Если резонатор по форме представляет собой консольную балку, а поглощаемая масса Δm при этом распределяется вдоль него равномерно, то сдвиг частоты Δf можно рассчитать по следующей простой формуле:

где f₀ и m₀ — начальные частота и масса наноустройства соответственно.

Из приведенной выше формулы нетрудно понять, что чувствительность резонатора будет высокой, если его масса маленькая, а частота большая. Углеродные нанотрубки идеально подходят для этой цели, обладая меньшими размерами и плотностью, а значит, и массой (равной по порядку величины 10^–21 кг) по сравнению с традиционными нанорезонаторами (10^–17 кг), изготовленными методом электронно-лучевой литографии (см. статью Zeptogram-Scale Nanomechanical Mass Sensing в журнале Nano Letters; в открытом доступе статью можно посмотреть здесь, PDF).

Именно такой сенсор массы на основе углеродной нанотрубки с двойными стенками и предложили ученые из Калифорнийского технологического института в своей работе An atomic-resolution nanomechanical mass sensor (многослойную нанотрубку такого типа — из вложенных друг в друга однослойных цилиндрических нанотрубок — называют «русская матрешка»).

Изображение одной из углеродных нанотрубок, использованной учеными для создания атомарных весов, можно увидеть на рисунке 1а. Ее характеристики таковы: внутренний диаметр D_i = 1,75 нм, внешний D_o = 2,09 нм, длина L = 254 нм, масса m_CNT = 2,33·10^–21 кг.

Итак, каков же принцип работы предложенного сенсора массы?

Углеродная нанотрубка закреплена одним концом на электроде и находится в камере, в которой создан высокий вакуум — давление 10^–10 мм рт. ст (рис. 1b). С вольфрамовой нити, расположенной на расстоянии d_CNT = 50,2 см от нанотрубки, испаряются атомы золота, массу которых и предлагается определить. Заслонка регулирует количество попадающих в резонатор атомов золота. Находящиеся на расстоянии d_QCM = 12,8 см перпендикулярно направлению испарения взвешиваемых частиц, кварцевые микровесы (QCM, quartz crystal microbalance) выполняют функцию калибровочного устройства для нанотрубки, контролируя равномерность испарения атомов золота. Иными словами, предназначение этих весов — убеждаться в постоянстве массового потока от вольфрамовой нити. Для детектирования механических колебаний резонатора ученые использовали уникальную особенность углеродных нанотрубок, заключающуюся в зависимости между ее механическими колебаниями и током автоэлектронной эмиссии (рис. 2). Как показали измерения, до открытия заслонки частота резонатора составила 328,5 МГц. Из соотношения между частотой резонатора и его массой (см. формулу выше) получаем, что поглощение одного цептограмма массы (1 цептограмм (цг) = 10^–24 кг) соответствует уменьшению частоты резонатора на Δf = 0,104 МГц (то есть чувствительность резонатора равна 0,104 МГц/цг).

Рис. 2. Участок схемы, с помощью которой по величине тока автоэлектронной эмиссии детектируют частоту механических колебаний нанотрубки. Рисунок из обсуждаемой статьи

В динамике работа сенсора массы выглядит так. С помощью кварцевых микровесов при закрытой заслонке исследователи убеждались в постоянстве массового потока атомов золота, испаряющихся с вольфрамовой нити. После этого ученые открывали заслонку, позволяя небольшому количеству атомов достичь углеродной нанотрубки. Далее заслонка закрывалась, и спустя некоторое время эксперимент повторялся вновь. Результаты опыта представлены на рис. 3, из которого видно, что, как и ожидалось, частота резонатора уменьшилась.

Рис. 3. a — изменение частоты резонатора (углеродная нанотрубка) со временем. Серые полосы соответствуют моментам времени, когда затвор не пропускает атомы золота в резонатор, белые полосы отвечают времени, когда затвор открыт, и атомы золота достигают поверхности нанотрубки. График во вставке на рисунке а демонстрирует зависимость скорости сдвига частоты резонатора от массового потока, фиксируемого с помощью кварцевых микровесов. b — график, подтверждающий с помощью кварцевых микровесов постоянство скорости испарения атомов золота с вольфрамовой нити. В эксперименте использовалась нанотрубка со следующими параметрами: D_o = 1,78 нм, D_i = 1,44 нм, L = 205 нм, m_CNT = 1,58·10^–21 кг. Добротность резонатора составляла порядка 1000. Рисунок из обсуждаемой статьи

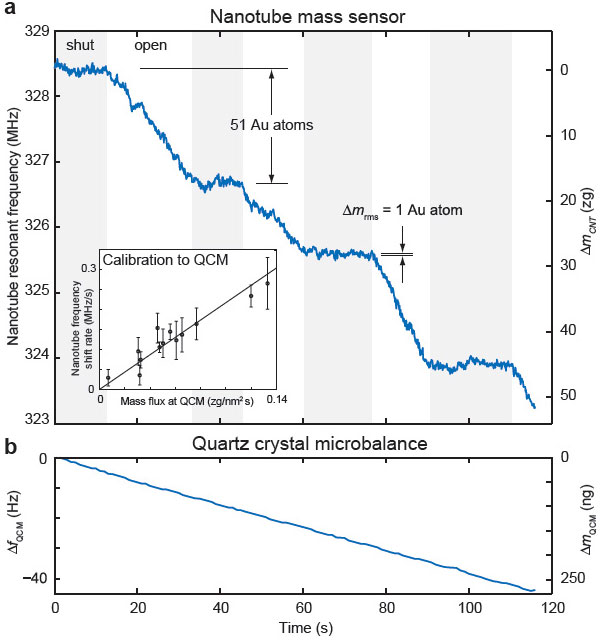
По резонансному сдвигу частоты исследователи определили (предполагая массу атома золота известной — 0,327 цг), что во время первого открытия заслонки углеродная нанотрубка «вобрала» в себя 51 атом золота (рис. 3a). Что самое поразительное и важное в этих экспериментах, так это то, что все данные получены и измерены при комнатной температуре! Никакого охлаждения до низких температур не происходило.

При такой температуре логично ждать высокого уровня шума атомного сенсора, а значит, и существенного ограничения его чувствительности. Ученым необходимо было уяснить: так ли это на самом деле?

Как видно из рис. 3a, частота резонатора очень слабо осциллирует, даже когда заслонка закрыта и поглощения частиц нанотрубкой не происходит. Эти мелкие осцилляции авторы назвали массовым шумом и связали его со статистическими флуктуациями в скорости поглощения атомов золота углеродной нанотрубкой. Именно уровень этого шума, который составил 0,13 цг/√Гц или 0,4 Au-атома/√Гц, и накладывает ограничение на чувствительность данного устройства.

Несколько слов о единицах измерения уровня шума — в частности, о кг/√Гц. Откуда появляется единица «квадратный корень из герца» (√Гц)? Рассмотрим в качестве примера тепловой шум — шум, который возникает из-за теплового движения зарядов в проводнике. Это движение зарядов приводит к тому, что на концах проводника с сопротивлением R возникает флуктуирующая разность потенциалов V, определяющаяся формулой Найквиста: , где k — постоянная Больцмана, T — температура и Δf — ширина частотного диапазона измерений (угловые скобки означают усредненное, среднее значение этого напряжения; если быть точным до конца, то среднеквадратичное значение). Теперь предположим, что в нашем распоряжении находится проводник с сопротивлением 100 Ом при температуре 100 К. Из формулы Найквиста рассчитываем величину, именуемую уровнем шума: 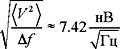. Означает это число следующее: если мы проводим измерения напряжения на проводнике в диапазоне, скажем, 100 Гц, то напряжение на нём «шумит» с величиной 74,2 нВ. То есть измерить напряжение в проводнике мы можем с точностью до указанного значения.

Аналогичное рассмотрение можно провести и для дробового шума, возникающего вследствие дискретности заряда q носителей тока. Уровень такого типа шума определяется из формулы Шоттки: . Например, для тока 1 А и частотной ширины измерений 1 кГц получаем приблизительно силу «шумящего» тока 18 нА.

Схожий подход для определения шума и, соответственно, чувствительности используют и в других измерительных устройствах. СКВИД (SQUID) — прибор для измерения очень слабых магнитных полей — имеет уровень шума порядка 1 фТл/√Гц (1 фТл (фемтотесла) = 10^–15 Тл). Как видим, чувствительность любого устройства, по сути, можно определять как единицу измерений этого устройства, деленную на корень квадратный из герца (√Гц), и ограничивается эта чувствительность уровнем шумов в конкретном измерительном приборе.

Такое значение шума эквивалентно способности прибора «почувствовать» массу единичного атома золота, поэтому ученые поставили перед собой обратную задачу — зная уровень шума нанорезонатора, определить массу атома золота. Для этого они провели аналогию в математическом описании дробового и массового шума и исходя из этого получили для массового шума формулу, определяющую его спектральную плотность. В эту формулу, помимо всего прочего (частота резонатора, его масса, скорость поглощения частиц углеродной нанотрубкой), входит и искомая величина — масса атома золота. Измерив уровень остальных возможных типов шумов в эксперименте (тепловой и дробовой шум), ученые смогли опытным путем определить спектральную плотность массового шума. А уже отсюда, с помощью упомянутого выше выражения, авторы без труда посчитали массу единичного атома золота: 0.29±0,05 цг, которая неплохо согласуется с точным значением 0,327 цг.

В общем, плюсы данного устройства очевидны:
    1) для определения массы не требуется ионизации взвешиваемой частицы, достаточно лишь направить частицу в резонатор (углеродную нанотрубку);
    2) по сравнению с используемыми масс-спектрометрами, новое устройство обладает большей чувствительностью;
    3) компактность устройства: оно не требует больших магнитов и длинных пролётных трубок, как в традиционных масс-спектрометрах.

Источник: K. Jensen, Kwanpyo Kim, A. Zettl. An atomic-resolution nanomechanical mass sensor // arXiv:0809.2126 (12 September 2008).

Юрий Ерин