Королевство кривых треугольников

Валерия Сирота
«Квантик»№3, 2024

Если вы уже начали учить в школе геометрию, то прошли или вот-вот изучите такую теорему: сумма углов треугольника равна 180°.

Эту теорему учат все школьники, знают все взрослые... И, однако, она не всегда верна! Как же такое может быть? А вот как: эта теорема верна для всех треугольников на плоскости. Но если рисовать их на искривленных поверхностях — она не работает!

Но как рисовать треугольники на искривлённых поверхностях? Ведь их стороны — это куски прямых, а на кривой поверхности прямых может и не быть? Впрочем, мы же все живём на кривой поверхности шара, и это ничуть не мешает нам говорить о прямом пути от дома до школы или даже из Москвы в Питер. Так что прямые найдутся, надо их только правильно определить.

Прямая (а точнее, геодезическая) на поверхности — это линия кратчайшего пути по этой поверхности из одной точки в другую. Есть кое-какие тонкости (см., например, статьи про конусы и цилиндры в «Квантике» №№8–10 за 2020 год), но пока нам достаточно и такого определения.

Теорема о сумме углов треугольника доказывается через параллельные прямые (рис. 1). Особенно легко, если уже знать теорему о внутренних накрест лежащих углах при параллельных прямых: проведём через вершину С прямую, параллельную АВ, тогда угол α равен углу A треугольника, а угол β равен углу В как внутренние накрест лежащие. Поэтому А + В + С = α+ β + С = 180°.

Рис. 1

Сфера и прямые на ней

Рис. 2

Если вы возьмёте нитку и натянете её между двумя любыми точками на поверхности мяча — это и будет кратчайший, прямой путь. Нитка пройдёт по «большому кругу», центр которого совпадает с центром мяча (проверьте!). На глобусе экватор и все меридианы — «большие круги», поэтому путь по ним — кратчайший. А вот параллели не годятся: если вы возьмёте две точки на одной параллели, например Москву и Читу, «прямая» — то есть геодезическая линия — пройдёт ближе к полюсу, чем параллель (рис. 2). А прямой путь из Санкт-Петербурга в Магадан и вовсе проходит через полуостров Таймыр и Карское море. Это легко проверить как с ниткой на глобусе, так и на Яндекс-картах (если вы им верите) с помощью инструмента «Линейка».

Рис. 3

Давайте для начала представим себе на Земле — или нарисуем на глобусе — какой-нибудь большой треугольник. Например, Северный полюс — Аккра — Сингапур. Чтобы измерить сумму его углов, нужно натянуть нитки на глобусе между тремя выбранными точками и измерить углы между этими нитками. Я специально выбрала Аккру и Сингапур, они почти на экваторе. Между ними нитка так по экватору и пойдёт. А из них на Северный полюс — по меридианам (рис. 3). Значит, два угла в этом треугольнике окажутся примерно по 90° — углы между экватором и меридианом. Это уже 180°, а ведь есть ещё третий угол: у Аккры долгота примерно 0°, у Сингапура около 100°. Итого, сумма углов треугольника приблизительно 90° + 90° + 100° = 280°!

Сфера — вся такая симметричная, со всех сторон одинаковая. Все её куски «выпуклы» одинаково и имеют одинаковую кривизну. Она называется ещё поверхностью постоянной положительной кривизны. Все треугольники на ней имеют сумму углов, бо́льшую 180°. Причём сумма эта зависит от размера (точнее, площади) треугольника: у совсем маленьких, почти плоских, она почти равна 180°, а чем больше треугольник, тем она больше. И от размера сферы зависит, конечно: треугольник той же площади на большей сфере оказывается ближе к плоскому, и сумма его углов меньше, чем на маленькой. Эллипсоид, сплюснутый, как мандарин, или вытянутый, как дыня, тоже имеет положительную кривизну, хоть и не постоянную, а меняющуюся от точки к точке. У нарисованных на дыне треугольников одинаковой площади суммы углов будут разными: на самой плоской части в середине только чуть-чуть больше 180°, а на сильно искривлённых участках — заметно больше. В этом смысле, одни участки дыни похожи на большую сферу, другие — на маленькую.

Эти одинаковые по площади треугольники можно даже использовать как «мерило кривизны»: чем больше сумма углов, тем более искривлённая в этом месте поверхность, тем больше у неё кривизна, тем на более маленькую сферу она в этом месте похожа.

Итак, сумма углов треугольника на плоскости равна 180°, а на сфере всегда больше. Интересно, как обстоят дела на других простых и понятных поверхностях — на цилиндре и конусе? В «Квантике» №№8–10 за 2020 год мы в них порядочно разобрались, научились делать их выкройки-развёртки и чертить на них геодезические линии... Не будем рассматривать цилиндр — с ним вы потом легко разберётесь сами — а займёмся сразу конусами.

Конус

Для начала посмотрим на конус, который получается сворачиванием полуплоскости — то есть берём лист бумаги, выбираем на одной из сторон точку и аккуратно склеиваем две половинки этой стороны друг с другом (рис. 4а). Пусть на конусе нарисован треугольник (рис. 4б). Мы можем «отойти от него подальше» и провести линию разреза — от вершины конуса вниз — так, чтобы она нигде этот треугольник не пересекла. Тогда после разрезания и разворачивания конуса получится «выкройка» с нарисованным на ней треугольником (рис. 4в), причём треугольник никак не пострадает: прямые линии останутся прямыми, углы тоже останутся прежними... — мы же не растягивали и не сжимали лист бумаги, только разрезали, и в близкой окрестности каждой вершины всё осталось как было до сворачивания. Значит, сумма углов треугольника как была, так и осталась 180°! Выходит, для «неправильной» суммы углов треугольника просто свернуть лист бумаги и сделать поверхность, «выпуклую в одном направлении», мало: чтобы получилось что-то интересное, нужна поверхность, «кривая в обе стороны».

Рис. 4

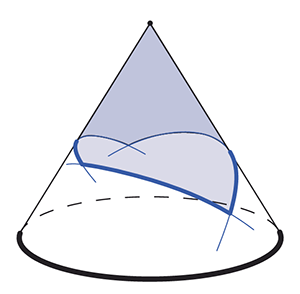
Рис. 5

Впрочем, кое-что интересное можно найти и здесь. Всегда ли мы можем провести разрез так, чтобы не задеть треугольник? Нет — мы не сможем это сделать, если треугольник содержит вершину конуса внутри себя, то есть если он «огибает» весь конус, как на рисунке 5. Можно, правда, спорить, считать ли эту штуку треугольником или нет... Однако, если это всё же треугольник, то какая у него сумма углов?

Рис. 6

Посмотрим сначала на самый симметричный из таких треугольников — треугольник, у которого все вершины лежат на одной и той же «параллели» конуса. Не волнуйтесь, стороны при этом лежат на совсем разных «прямых» — они ведь все проходят выше параллели. Получается «корона», как на рисунке 6. А теперь наберёмся смелости и разрежем нашконус... прямо по одной из вершин треугольника! При этом она раздвоится — придётся рисовать точку А и на левом, и на правом краю развёртки. Получается рисунок 7. Все тре угольники на этом рисунке — равносторонние. Значит, угол при каждой вершине такого треугольника равен 120°: у вершин В и С это видно сразу, а для вершины А нужно учесть, что при сворачивании конуса углы ОАВ и ОА'С состыкуются. Итак, сумма углов этого треугольника 120° ⋅ 3 = 360°.

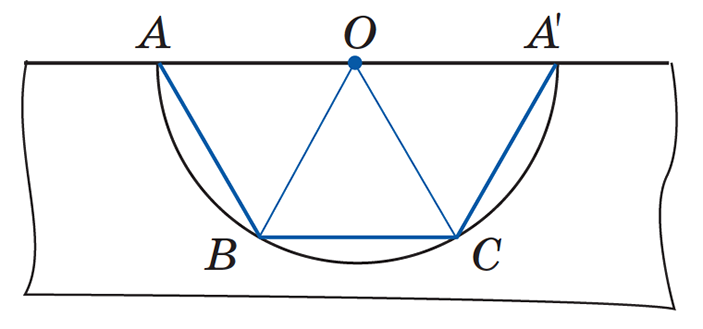
Рис. 7

Между прочим, у таких «обхватывающих» треугольников есть и ещё одно интересное свойство: у них возможны углы больше, чем 180°.

Обратите внимание: ситуация здесь не такая, как на сфере. Там были разные треугольники с разной суммой углов, она зависела от размера треугольника. Здесь — всего два типа треугольников: обычные плоские, у всех сумма 180° — и «заключающие в себе вершину», у всех сумма углов вдвое больше. Это потому, что вся кривизна здесь не размазана равномерно, как по сфере, а запрятана в одну-единственную точку — вершину конуса, а в остальных точках кривизна нулевая. И эта единственная точка или уж попадает внутрь и «кривит» треугольник, или нет.

Рис. 8

Задача 3. Разберитесь с произвольным конусом — который получается сворачиванием не полуплоскости, а сектора с углом α (рис. 8). (Угол α может быть и больше 180°.) Какие суммы углов треугольников получаются на нём?

Художник Алексей Вайнер

Окончание следует