Окружность девяти точек
Александр Блинков
«Квантик» №4, 2023
Познакомимся с одним из красивых фактов геометрии треугольника — теоремой об окружности девяти точек, называемой ещё окружностью Эйлера.
Теорема. Середины сторон треугольника, основания его высот и середины отрезков, соединяющих ортоцентр (точку пересечения высот) с вершинами треугольника, лежат на одной окружности (рис. 1).
Мы приведём один из самых простых способов её доказать. Нам понадобятся несколько фактов из школьного курса геометрии:
1. Средняя линия треугольника параллельна его стороне (рис. 2).
2. Две прямые, соответственно параллельные перпендикулярным прямым, перпендикулярны (рис. 3).
3. Точка С лежит на окружности с диаметром АВ тогда и только тогда, когда угол АСВ прямой (рис. 4).
4. Диагонали прямоугольника являются диаметрами его описанной окружности (рис. 5).

Теперь мы готовы доказать теорему.

Доказательство. Рассмотрим ос троугольный тре угольник АВС и его высоты, пересекающиеся в точке H (чтобы не загромождать чертёж, полностью проведём только высоту ВВ1). Пусть K и L — середины сторон АВ и АС, а P и Q — середины отрезков BH и CH (рис. 6а).
Заметим, что KL — средняя линия треугольника ВАС, значит, KL || BC, а PQ — средняя линия треугольника ВHС, значит, PQ || BC. Поэтому KL || PQ. Аналогично, KP и LQ — средние линии тре угольников АВН и ACН, поэтому KP || AH || LQ. Тогда стороны четырёхугольника KLQP соответственно параллельны перпендикулярным прямым ВС и AH, то есть KLQP — прямоугольник.
Рассмотрим окружность, описанную около KLQP, его диагонали — диаметры этой окружности. Угол РВ1L, опирающийся на диаметр PL, прямой, поэтому В1 тоже лежит на этой окружности.
Таким образом, уже доказано, что пять из девяти точек лежат на одной окружности.
Рассмотрим теперь вместо точек L и Р середины М и Т отрезков ВС и АН, а вместо точки В1 — основание А1 высоты, проведённой из вершины А (рис. 6б). Аналогично доказывается, что KMQT — прямоугольник. Но он имеет общую диагональ KQ с прямоугольником KLQP, поэтому их описанные окружности совпадают, то есть М и Т лежат на нашей окружности. Точка А1 лежит на ней же, так как диаметр ТМ виден из А1 под прямым углом.
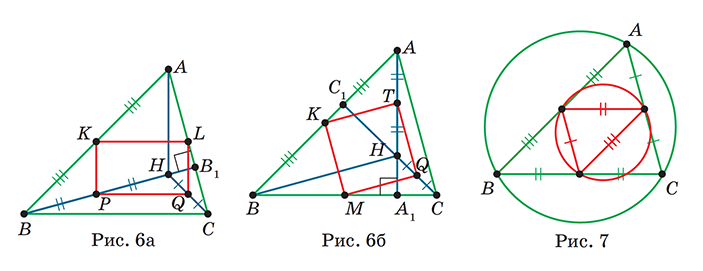
Осталась последняя точка: основание С1 высоты, проведённой из вершины С, которая лежит на той же окружности, так как QKC1Q = 90° (KQ — диаметр).

Случай остроугольного треугольника разобран. Прямоугольники KLQP и KMQT часто называют прямоугольниками Эйлера. Понятно, что существует ещё один такой прямоугольник: LMPT.
Найдём теперь радиус окружности девяти точек. Пусть R — радиус описанной окружности треугольника АВС. Заметим, что срединный треугольник (его вершины — середины сторон ABC) вписан в окружность девяти точек (рис. 7). Но его стороны в два раза меньше сторон исходного, поэтому он подобен треугольнику АВС с коэффициентом 0,5. Значит, радиус окружности девяти точек равен 0,5R.
Отметим, что мы доказали теорему для остроугольного треугольника. Нужно ли отдельно рассматривать случай тупоугольного треугольника? Для ответа на этот вопрос заметим, что если Н — ортоцентр остроугольного треугольника АВС, то А — ортоцентр тупоугольного треугольника ВНС (рис. 8). Действительно, НА1, ВС1 и СВ1 — высоты треугольника ВНС. При этом у треугольника ВНС та же самая окружность девяти точек, так как середины K и L сторон АB и AС просто меняются «ролями» с серединами P и Q отрезков ВН и СН, а «роли» остальных точек не меняются!
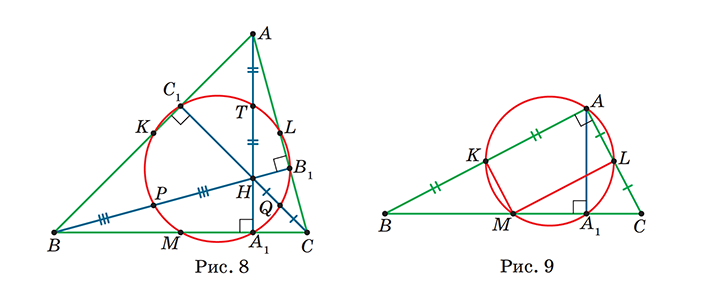
Точки А, В, С и Н, любая из которых является ортоцентром треугольника, образованного тремя другими, обычно называют ортоцентрической четвёркой. Таким образом, у четырёх треугольников АВС, ВНС, АНВ и АНС окружность девяти точек одна и та же.

Разберём, наконец, случай прямоугольного треугольника АВС (QА = 90°).
Проведём окружность через середины K, L и М его сторон и убедимся, что она соответствует окружности девяти точек (рис. 9).
Действительно, KMLA — прямоугольник, поэтому эта окружность проходит через вершину А. То, что на окружности лежит основание А1 высоты, доказывается как и выше. Но точек всего пять, где же остальные?
Их и не должно быть. Ведь А — ортоцентр треугольника, в этой точке совпадают основания двух высот и она же — «вырожденная» середина отрезка, соединяющего эту вершину с ортоцентром. А середины K и L сторон АВ и AС совпадают с серединами отрезков, соединяющих вершины В и С с ортоцентром.
Напоследок вернёмся к случаю непрямоугольного треугольника. Как мы видели, шесть из девяти точек на окружности Эйлера разбиваются на три пары диаметрально противоположных. Выберем любую из этих шести точек и найдём расстояния до оставшихся трёх точек. Докажите, что два расстояния из трёх совпадут.
Художник Алексей Вайнер


















