Пиковое занятие

Игорь Акулич
«Квантик» №12, 2022

— Сегодняшнее наше занятие — Пиковое. Но не надейтесь, что я сейчас достану из кармана колоду карт. Наше занятие — Пиковое с большой буквы. И названо в честь австрийского математика XIX– XX веков Георга Александра Пика. Он занимался самыми разными проблемами, порой очень сложными. Математикам известны матрица Пика, интерполяция Пика и многое другое. Но наиболее широко он прославился формулой Пика, позволяющей определять площади многоугольников на квадратной сетке.

Рис. 1

Поясню вкратце для тех, кто не в курсе. Пусть бесконечная плоскость разбита вертикальными и горизонтальными прямыми на одинаковые квадраты площади 1 каждый. Назовём узлами вершины квадратов и нарисуем произвольный многоугольник, все вершины которого лежат в узлах. Стороны многоугольника не обязаны быть вертикальными или горизонтальными (хотя это и допускается). Подсчитаем количество В узлов, попавших строго внутрь многоугольника, и количество Г узлов, оказавшихся на его границе. Последними будут, безусловно, все вершины многоугольника (по условию), а возможно, и ещё какие-то узлы, попавшие на стороны. Так, пятиугольник на рисунке 1 имеет 8 узлов внутри (отмечены красным), то есть В = 8, и 9 узлов на границе (синие), то есть Г = 9.

Оказывается, площадь любого многоугольника с вершинами в узлах зависит только от значений В и Г и вычисляется по формуле

S = В + 0,5Г − 1.

Это и есть знаменитая формула Пика. Именно её красота покорила весь мир. Говорят, в Германии она даже включена в школьную программу (у нас пока нет). Для пятиугольника на рисунке 1 получаем

S = 8 + 0,5 · 9 − 1 = 11,5.

Доказательство формулы Пика не простое, но и не слишком сложное. Eго можно найти на страницах и «Кванта», и «Квантика». Мы на это отвлекаться не будем — кто любопытен, сам найдёт и прочтёт. Отметим только, что аналоги формулы Пика имеются и для других видов бесконечной сетки — например, треугольной.

— Мы же с вами займёмся другим делом — осуществим переход от точек к отрезкам.

— Это как?

Рис. 2

— Сейчас объясню. Формула Пика носит, образно говоря, точечный характер, ибо в ней мы подсчитываем точки, лежащие внутри и на границе многоугольника. Давайте аналогичные действия произведём с отрезками самой сетки, попавшими внутрь многоугольника либо совпавшими с какими-то его сторонами. Сначала — по горизонтали. В рассмотренном нами пятиугольнике выделим красным кусочки горизонтальных линий сетки, попавшие внутрь, и синим — горизонтальные стороны (рис. 2). А теперь, по аналогии, подсчитаем суммарную длину В отрезков сетки, попавших внутрь многоугольника (красных) и суммарную длину Г отрезков сетки, совпадающих с его сторонами (синих). В нашем случае красных отрезков четыре. Верхний, как нетрудно понять, равен 1,5 — нецелому числу. Не очень радует, но ничего не поделаешь, придётся терпеть. Зато второй сверху — ровно 3. Третий тоже нецелый — 3,5. Четвёртый — снова 3. Итого В = 1,5 + 3 + 3,5 + 3 = 11. Синий же отрезок лишь один, длины 1, поэтому Г = 1. Так вот, оказывается, площадь любого многоугольника тоже зависит лишь от В и Г и вычисляется по формуле:

S = В + 0,5Г.

Почти точное совпадение с формулой Пика. Например, для нашего пятиугольника

S = 11 + 0,5 · 1 = 11,5.

— А если взять вертикальные линии сетки?

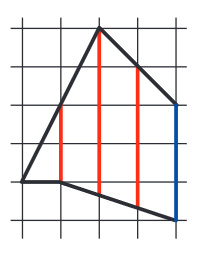
Рис. 3

— Попробуем! Здесь (рис. 3) получается лишь 3 красных отрезка, но с определением их длин придётся повозиться. Самый левый равен 2. А вот дальше... Средний, как видно, равен 4 с небольшим, а правый — 3 с небольшим (правда, с другим небольшим). И эти небольшие добавки порождает нижняя сторона нашего пятиугольника. Как же нам их определить?

— Я понял! Нижняя сторона — это же диагональ прямоугольника 1 × 3. Она делит его на симметричные части, поэтому вторая добавка дополняет первую до единицы!

Рис. 4

— Отлично! Значит, сумма длин среднего и правого красных отрезков равна 4 + 3 + 1 = 8. Синий же отрезок равен 3. Впрочем, с синими отрезками проблем быть не может — их длины всегда целые (сумеете это доказать?). Теперь мы можем определить площадь пятиугольника и третьим способом — по длинам вертикальных отрезков. Здесь В = 2 + 8 = 10 и Г = 3. Поэтому

S = 10 + 0,5 · 3 = 11,5.

Можете «испытать» и другие многоугольники и убедиться, что всегда получается верный ответ. Поэтому мы можем с гордостью назвать нашу формулу линейной формулой Пика (или, если хотите, отрезковой).

— А доказательство у вас есть?

— Да, и весьма простое. Изложу его для горизонтальных отрезков (а для вертикальных можно повернуть картинку на 90°). Разрежем многоугольник горизонтальными линиями сетки на «дольки». Каждая такая долька — многоугольник, ограниченный с двух сторон прямыми, расстояние между которыми равно 1. Все его вершины непременно лежат на этих прямых — ведь узлы все находятся на горизонтальных прямых, и между соседними прямыми узлов нет. А раз так, «ассортимент» возможных видов долек очень невелик. Это может быть трапеция, параллелограмм либо треугольник — и обязательно с единичной высотой.

Если это трапеция с основаниями a и b, то площадь её равна \(\frac{a+b}{2}\cdot 1=\frac{a}{2}+\frac{b}{2}\). Для параллелограмма — то же самое, только здесь в придачу ко всему a = b. И для треугольника формула верна — надо лишь учесть, что или a = 0, или b = 0. Так что площадь каждой дольки равна сумме половин отрезков, ограничивающих её сверху и снизу. И потому площадь всего многоугольника есть сумма таких половин для всех долек. Когда отрезок общий для двух соседних долек, его половина войдёт в сумму дважды, и в этой сумме, таким образом, участвует просто длина отрезка. А если отрезок крайний — то его половина и останется. Но ведь это и есть описание приведённой формулы: сумма длин отрезков, попавших внутрь многоу гольника, плюс полусумма длин отрезков, попавших на его границу (то есть совпадающих с какими-либо сторонами). Доказательство закончено.

Вижу, все согласны, кроме вот этого молодого человека. Что же вас не устраивает? − Да нет, устраивает, но... кое-что здесь лишнее.

— Это как?

— В доказательстве не использовался тот факт, что сетка — квадратная. Учитывалось только разбиение плоскости параллельными прямыми на слои единичной ширины. И потому данная формула, как мне кажется, пригодна и для многоугольника, все вершины которого лежат на каких-то параллельных прямых, разбивающих плоскость на полоски равной ширины.

— Справедливо! Поэтому давайте окончательно сформулируем теорему так.

— Ну как, теперь сойдёт?

— Вполне.

— Вот и прекрасно. А вам спасибо за своевременную критику. На этом можно бы и откланяться, но сначала предложу вам для размышления задачу¹:

К читателям. Решите и вы эту задачу, используя линейную формулу Пика.

Художник Мария Усеинова

¹ Автор задачи — Г. Гальперин. Задача была предложена в 10 классе на Московской математической олимпиаде 2000 года, а также в 10 — 11 классах на Турнире городов 1999 — 2000 года.