И снова про коники: окончание

Валерия Сирота
«Квантик»№9, 2023

Окончание. Начало читайте здесь.

Эллипс — парабола — далее везде. Фокус с фокусами

Разобравшись с задачками, Данька спросил: — А вот если я буду всё сильнее наклонять плоскость — я ведь получу всё более вытянутые эллипсы, да? И потом они превратятся в параболу?

— Конечно, но какого эллипсы будут размера — зависит от того, как ты поднимаешь или опускаешь плоскость, то есть как при этом меняется расстояние от плоскости до вершины конуса. Можно менять так, чтобы «начало» у всех эллипсов было в одной и той же точке и конуса, и плоскости (рис. 9, а). А потом все плоскости с нарисованными на них кониками совместить. В этом случае, если конус широкий (угол раствора больше 90°), эллипсы, возникающие между появлением окружности и параболы, окажутся внутри параболы, а окружность — внутри эллипсов (рис. 9, б); если конус узкий — эллипсы возле общей точки будут сначала «толстеть», а потом «худеть» (но поперечный размер эллипсов в любом случае растёт) (рис. 9, в).

Рис. 9

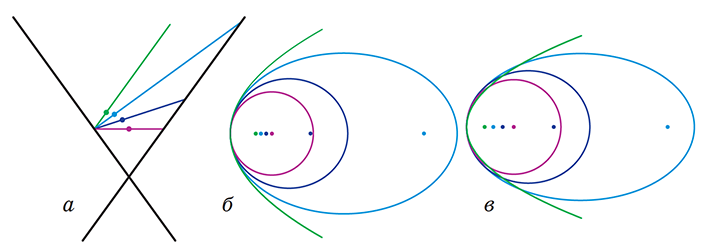
— А если так менять, чтобы фокусное расстояние всё время оставалось одним и тем же? — Можно. Но тогда мы не увидим ни настоящей окружности — она должна получиться бесконечно большой, ни параболы — она была бы бесконечно узкой, сольётся с отрезком (рис. 10).

Рис. 10

— Как это — парабола превращается в отрезок?

— На самом деле не в отрезок, а в прямую... При таком способе сдвигания плоскости горизонтальная плоскость (и окружность) была бы бесконечно далеко вверху, а по мере увеличения наклона она бы «спустилась» до самого низа, и при таком угле, который нужен для параболы, проходила бы уже через вершину конуса. Видишь — на нашей картинке сечение всё ближе и ближе к образующей конуса. Когда совсем сольётся с ней — толщина у нашего эллипса исчезнет, зато и верхний край исчезнет, отрезок превратится в луч. Как будто бесконечно узкая парабола. Ещё и снизу «хвост» отрастёт, потому что наша плоскость уже и нижнюю часть конуса задела... В общем, это так себе способ: ни окружности, ни параболы не получается.

Давай лучше так двигать плоскость, чтобы угол наклона менялся, а расстояние ρ при этом оставалось постоянным — как на рисунке 11 слева. Тогда можно совместить картинки всех полученных эллипсов так, что и один из фокусов, и ближняя к нему точка будут закреплены, а второй фокус уползает вдаль... и эллипс превращается в параболу. А потом — когда ещё сильнее наклоняем — в гиперболу! Что происходит сo вторым фокусом? Он теперь приближается из бесконечности, но с другой стороны (рис. 11)!

Рис. 11

— Круто! Гипербола — это вывернутый через бесконечность эллипс! У которого середина застряла на бесконечности.

— Кстати, я всегда так объясняла себе, почему у параболы директриса «вместо» второго фокуса. Давай проведём через дальний фокус эллипса прямую, перпендикулярную главной его оси (рис. 12). Возьмём какую-нибудь точку М вблизи первого, ближнего фокуса и сравним d2 — расстояние от неё до дальнего фокуса с расстоянием d2´ до этой перпендикулярной прямой. Если эллипс сильно вытянут, то эти два расстояния почти равны. Правда же? — «толщина» эллипса несущественна по сравнению с его «длиной».

Получается, что наш очень вытянутый эллипс вблизи первого фокуса задаётся таким условием: сумма расстояний от любой точки до первого фокуса и до прямой, проходящей через второй фокус, одна и та же для всех точек: d1 + d2´ = c. Но, поскольку эта новая прямая уже очень далеко и при удлинении эллипса уходит всё дальше, мерять расстояние до неё неудобно. А ведь можно вместо этого не прибавлять, а отнимать расстояние до какой-то другой прямой, параллельной ей, но находящейся слева от эллипса! (Чтобы все точки эллипса были по одну и ту же сторону от неё.) И такая разность тоже будет одна и та же для всех точек, потому что d1 — d3 = d1 + d2´ — d23 = c — d23: она отличается от той суммы, что была раньше, на постоянное число — расстояние d23 между прямыми. Ну а уж раз мы можем выбрать эту прямую и это расстояние как угодно, ничего не стоит подобрать её так, чтобы разность равнялась нулю! Конечно, для длинного эллипса это всё верно только приблизительно. Но чем более вытянутый эллипс, тем точнее, a для параболы — совсем точно.

Рис. 12

Для знатоков координат

— А вот ещё вопрос, — сказал Данька. — У нас в школе тоже ведь были и параболы, и гиперболы. Но это какие-то не те, что ли?

— Почему же не те? Те самые! Чтобы в этом убедиться, реши такую задачку:

— Опять теорема Пифагора мне в помощь, да? Но у всех наших парабол, как мы выяснили, только один параметр, которым они могут отличаться, — расстояние ρ от фокуса до ближайшей точки (или 2ρ — от фокуса до директрисы). А в школе писали общее уравнение параболы аж с тремя коэффициентами: y = ax2 + bx + c. Куда их столько, этих буковок? Зачем они нужны, если это всё та же самая парабола?

— А на этот вопрос отвечать не буду! Это ты и сам прекрасно можешь догадаться, если хорошо понял, как устроены графики разных уравнений и что с ними можно делать. Пусть это будет

А вот гиперболы школьной программой обижены. На самом деле они, как и эллипсы, управляются двумя параметрами. Например, фокусным расстоянием 2f и всё тем же ρ. Но, как мы видели, при разных значениях этих параметров получаются гиперболы, расходящиеся вдали под разными углами. В школе же изучают только те из них, у которых этот угол (угол между асимптотами) равен 90°. Поэтому для справедливости давай решим про гиперболу две задачки посложнее! Решать «в лоб» через теорему Пифагора — сложно. Но можно применить хитрость вроде той, которая далёкий фокус эллипса превращает в директрису параболы: для этого надо рассмотреть далёкую точку гиперболы...

— Ну а теперь, когда мы почти во всём разобрались, — удовлетворенно сказал Данька, — мы сможем быстренько понять, почему же планеты так летают?

— Э, Данька... До этого нам ещё так далеко... Давай пока считать, что просто — чудо!

Автор благодарит Глеба Бобкова-Нойманна (школа 179) за полезные замечания.

Художник Алексей Вайнер