И снова про коники

Валерия Сирота
«Квантик»№8, 2023

Когда я вернулась из своего первого горного похода — с Фанских гор, — мне позвонил папин друг, бывший альпинист, и замирающим от предвкушения голосом спросил: «Ну как?»

А я уже устала к этому времени от впечатлений и от собственных рассказов о них и ответила без особого подъёма: «Ну, здорово!»

— То есть как?! — воскликнул он, и круглые от удивления глаза его так и просвечивали сквозь телефонную трубку. — Ты что, не видела там красные горы, из которых синие осыпи?!

И тут, спустя неделю после последнего фанского перевала, эта картина вдруг снова встала у меня перед глазами, и я поняла наконец, что ведь да! — не «красиво», не «здорово», а — потрясающе!

Эту историю я вспомнила недавно, когда ко мне пришёл Данька и сказал — без восторга, как мне показалось, — что прочитал в «Квантике» про конические сечения.¹

Рис. 1

— Как! — возопила я. — Тебе показали чудо, а ты даже не удивился?!

— А...э...а какое чудо? — Данька был явно озадачен моим напором.

— Ну как же, ты режешь конус плоскостью под бог знает каким углом, наперекосяк, а в сечении получается симметричный эллипс!

— Э... действительно. С гиперболой даже ещё страннее, два её куска в совсем разных местах от конуса отрезаются, а всё равно одинаковые (рис. 1)...

— Или откуда видно, что эллипс можно растянуть вдоль одной из осей, и получится окружность? Или, например, то, что планеты и кометы летают именно по эллипсам и гиперболам. Почему — именно по коническим сечениям? Где там в космосе конусы, из которых эти эллипсы вырезаются?

Рис. 2

— ...

— Или однополостный гиперболоид — тот, из которых Шуховская телебашня. Ведь его, по идее, получают, вращая гиперболу вокруг оси. С чего вдруг он оказался состоящим из прямых?! И это тебе там ещё не рассказали, что есть гиперболический параболоид (рис. 2), где одна парабола по другой ездит. (Он похож на седло, и это в его форме сделаны чипсы «Принглс».)² Его вертикальной плоскостью пер есечёшь — получишь параболу, пересечёшь горизонтальной — гиперболу, и его тоже можно сложить из прямых!

Рис. 3

— Или эта история с шариками. Кладёшь в конус шарик, сверху кидаешь плоскость, сверху ещё шарик — и вуаля! Вот они, фокусы эллипса (рис. 3)...

— Ну, это как раз понятно! Это из теоремы получается.

— Всё равно же чудо, разве нет? Но здорово, что ты понял теорему.

Как выбрать конус

— Я другого не понял. Вот есть эллипс. Как узнать, из какого конуса он сделан?

— А никак. Любой эллипс можно получить из любого конуса!

— Как так?! Конусы же разные, у них угол можно менять.

— Ну вот окружность, например, можно вырезать из любого конуса, да? Причём любую окружность, какого хочешь размера. Теперь давай с эллипсом разберёмся. У него всего два параметра: например, длина большой полуоси (половина «длины эллипса») a и ρ — расстояние от фокуса до ближайшей точки эллипса (рис. 4). Эти два параметра можно подобрать, меняя наклон режущей плоскости и её «высоту» над вершиной конуса (рис. 5). Угол раствора конуса при этом может быть любой.

Рис. 4

Рис. 5

— А, да! А у параболы — всего один параметр, ρ — расстояние от фокуса до ближайшей точки параболы, он же половина расстояния от фокуса до директрисы. И только один параметр «управляет» тем, какая парабола получится: ведь у всех плоскостей, вырезающих из конуса параболу, наклон один и тот же, остаётся двигаться вверх-вниз (рис. 6)...

— А у гиперболы тоже два параметра, но тут есть хитрость. Видишь ли, — это отдельный замечательный факт! — вдали расходящиеся ветви каждой гиперболы стремятся к некоторым двум прямым (рис. 7).

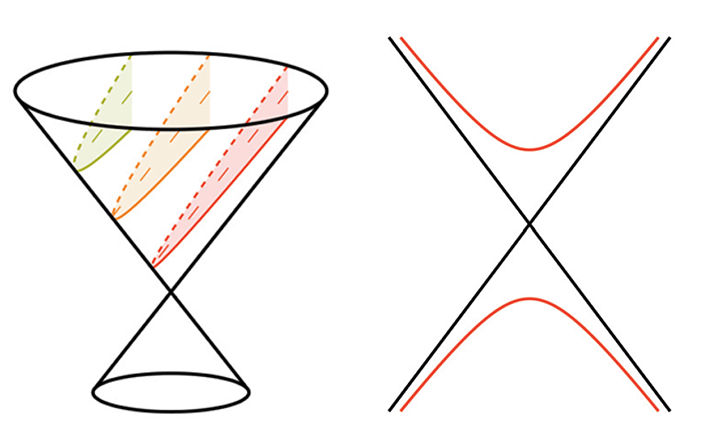
Рис. 6, рис. 7

Чем дальше от центра гиперболы, тем ближе её ветви к этим прямым, называемым асимптотами. Так вот, угол между этими самыми асимптотами гиперболы не может быть больше, чем угол раствора конуса, из которого её вырезали. Поэтому для каждой гиперболы подойдёт не любой конус, а только достаточно сильно (для неё) раскрытый. Кстати, вот тебе по этому по воду

А вот ещё задачка, и, между прочим, простая!

Рис. 8

И, раз мы уже нарисовали столько буковок на картинке про эллипс, давай напишем ещё одну: f = a — ρ — расстояние от фокуса эллипса до его центра (рис. 8). Кстати, 2f — это расстояние между двумя фокусами, оно так и называется — фокусное расстояние. Так вот, ты ведь знаешь теорему Пифагора?³ Тогда вот тебе ещё третья задачка:

Окончание следует

Художник Алексей Вайнер

¹ Две статьи Ф. Нилова «Эллипс, гипербола и парабола» и «Два века теоремы Данделена», «Квантик» № 2 и 3 за 2023 год, и подборка задач «Коники вокруг нас», «Квантик» № 3 за 2023 г.

² См. статью Н. Андреева и М. Прасолова «Линейчатые, но не плоские», «Квантик» № 9 за 2021 г.

³ Теорема Пифагора: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов. В переводе на человеческий язык: если длину самой большой стороны прямоугольного треугольника умножить на саму себя, а длины двух меньших сторон тоже умножить каждую на себя и потом сложить, то получится два одинаковых числа.