Два века теоремы Данделена

Фёдор Нилов
«Квантик» №3, 2023

Жерминаль Данделен

Ещё древние греки (например, Менехм и Аполлоний) знали, что эллипс, гиперболу и параболу можно получить, пересекая конус плоскостью. Но они, видимо, не знали чисто геометрического доказательства.

В 1822 году бельгийский инженер и математик Жерминаль Данделен такое доказательство придумал! Мы разберём его для случая цилиндра: любое сечение цилиндра наклонной плоскостью (не параллельной оси цилиндра) будет эллипсом.

Оригинальная идея Данделена следующая: впишем в цилиндр две одинаковые сферы, касающиеся данной плоскости, одна — сверху (в точке P), другая — снизу (в точке Q), как на рисунке 1.

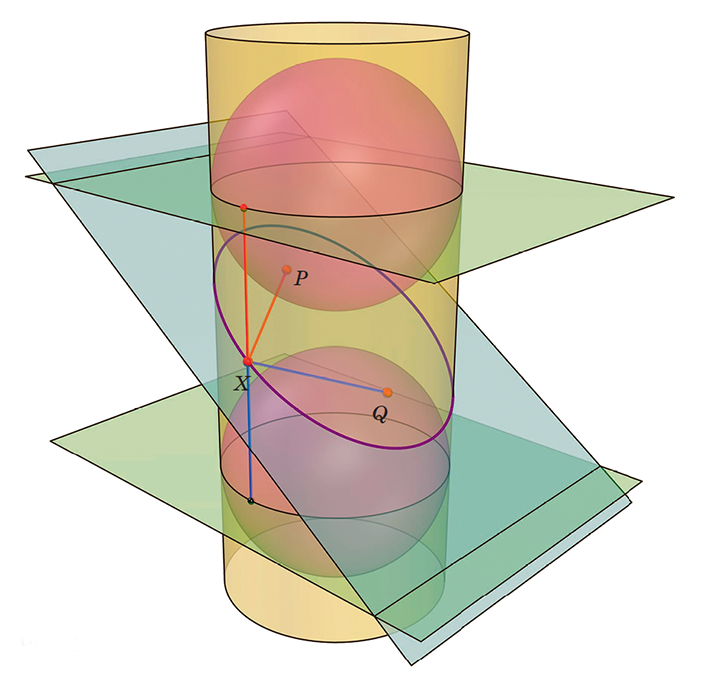
Рис. 1

Оказывается, сечение — это эллипс, фокусы которого — точки P и Q! Действительно, возьмём какую-нибудь точку X на сечении. Расстояние XP равно вертикальному отрезку, соединяющему X с экватором верхней сферы — ведь это две касательные, проведённые к сфере из одной точки. Аналогично, XQ — расстояние от X до экватора нижней сферы. Поэтому сумма расстояний от X до точек P и Q всегда одна и та же: она равна расстоянию между экваторами сфер!

Аналогично можно доказать, что сечения конуса плоскостями, не проходящими через вершину, — это коники: эллипсы, гиперболы, параболы. Их фокусы — снова точки касания сфер Данделена с плоскостью сечения.

А как увидеть их директрисы? Точки касания сферы Данделена с конусом лежат в горизонтальной плоскости. Прямая, по которой эта горизонтальная плоскость пересекается с плоскостью сечения, и есть директриса (рис. 2, а). Это доказал в 1829 году ирландский математик Пирс Мортон.

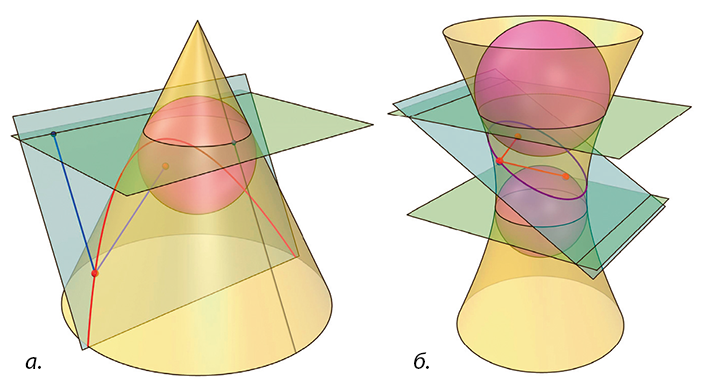
Рис. 2

В 1826 году Данделен заметил, что конструкцию со вписанными сферами можно применить и для однополостного гиперболоида вращения — эта поверхность получается вращением гиперболы относительно её оси симметрии, перпендикулярной линии фокусов (рис. 2, б). Снова сечения будут кониками, фокусы которых — точки касания сфер Данделена с плоскостью сечения, а директриса находится аналогично предыдущему случаю.

Дело в том, что однополостный гиперболоид тоже можно получить, вращая вокруг оси прямую¹ (рис. 3). Поэтому работает практически такое же рассуждение, что и для цилиндра с конусом.

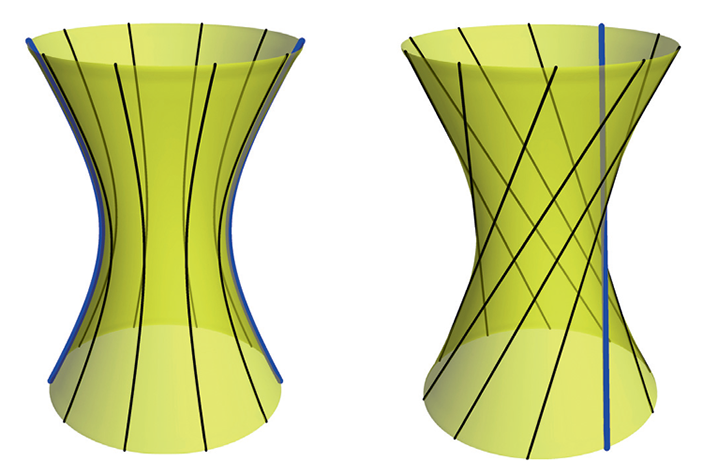
Рис. 3

На других поверхностях, получающихся вращением коники относительной одной из её осей симметрии, никаких прямых нет. Но теорема, аналогичная теореме Данделена, всё равно верна! Доказательство можно прочитать в статье автора в журнале «Квант», №10 за 2022 год. На рисунке 4 показан случай эллипсоида; анимации и больше красивых картинок можно найти на сайте «Математические этюды»².

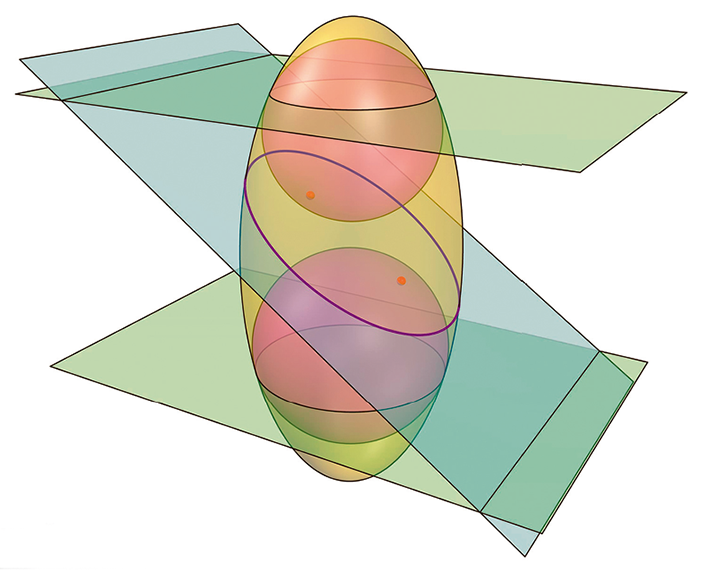
Рис. 4

Художник Мария Усеинова

¹ См. статью Н. Андреева и М. Прасолова «Линейчатые, но не плоские» в «Квантике» №9 за 2021 год.

² Сферы Данделена. Математические этюды.