Четырёхмерный кубик
Валерия Сирота
«Квантик» №7, 2022

Когда я была маленькой, мама и папа научили меня рисовать кубик. Наверное, вы все знаете: нужно сначала нарисовать квадрат — это передняя сторона кубика, которая «смотрит на нас»; потом провести из каждой вершины (угла) квадрата отрезки одинаковой длины и в одном и том же направлении — это горизонтальные рёбра кубика, которые ориентированы «от нас». Дальше четыре конца этих отрезков соединяем, получается ещё один квадратик — это задняя грань кубика. Вот и всё! Получился вид «со стороны передней грани и чуть сверху-сбоку». Если кубик не проволочный, а «сплошной» (непрозрачный), нужно стереть или лучше сделать пунктирными рёбра, которые скрыты за тремя ближайшими гранями — на рисунке 1 это передняя, верхняя и правая.
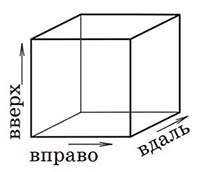
Проще простого, да? Но мои родители были математики. Поэтому они на этом не остановились и научили меня рисовать ещё и четырёхмерный кубик.
Это тоже оказалось просто! Надо только разобраться, что такое это четырёхмерье. Мы все живём в трёхмерном мире. Потому что у нас есть три независимых направления, вдоль которых мы можем перемещаться или хотя бы смотреть на разные вещи: вперёд-назад, вверх-вниз и вправо-влево. Вперёд-назад — считается за одно направление, потому что движения «туда» и «обратно» не независимы, а противоположны друг другу: одно может «отменить» действие другого, и, пройдя шаг вперёд, а потом шаг назад, вы вернётесь в ту же точку. А вот сделав шаг вправо, а потом несколько шагов вперёд, вы в ту же точку не вернётесь. Направление «по диагонали» тоже не независимое — это комбинация уже имеющихся. Ведь можно пройти по диагонали вверх-направо, а можно вместо этого пройти сначала вверх, а потом направо, и прийти в ту же точку (рис. 2).

Рис. 2
Можно представить себе двумерных муравьишек, живущих в плоскости. Например, нарисованных на экране компьютера. (Для определённости давайте считать, что плоскость вертикальна.) У них только два независимых направления, вверх-вниз и влево-вправо, выйти из плоскости они не могут. Cложная у них жизнь: если встретятся двое на дорожке, то, чтобы идти дальше каждому своей дорогой, придётся одному через другого перепрыгнуть. Или как им открывать двери в домах? Ещё сложнее жизнь у одномерных червяков, живущих на линии. Они вообще не разминутся при встрече, ползают только друг за другом... и если построят стенку (точку на линии), за неё никто не проникнет, никаких дверей нет.

Но сейчас речь не о них, а о других воображаемых (а может, и нет?) существах, живущих в мире с четырьмя измерениями. Кроме направлений вверх-вниз, вправо-влево и вперёд-назад у них есть ещё одна пара, ещё одно направление, которое мы и представить не можем, и даже названия для этого у нас нет. Так же как двумерные, плоские человечки не могут представить, что есть что-то «снаружи» их листа бумаги.
Но — удивительно! — хоть представить и нельзя, а нарисовать можно. Ведь трёхмерный куб тоже не помещается в двумерную плоскость, но мы ухитряемся нарисовать его на ней. Просто мы выбираем направление на плоскости, которое изображает третье измерение; те самые параллельные друг другу наклонные палочки на рисунке 1 — рёбра «от нас» — как раз ориентированы вдоль этого третьего направления. На плоскости оно совсем не независимое, но мы «забываем» об этом, чтобы увидеть в нарисованном наборе палочек не плоскую фигурку, а объёмный кубик.

Рис. 3
Чтобы показать на плоскости четвёртое измерение, нужно просто выбрать ещё одно направление, которое его изображает. Да и какая для плоскости разница — третье измерение или четвёртое? Они всё равно в неё оба не помещаются.
Итак, рисуем четырёхмерный кубик. По дороге вспоминаем, как мы рисовали трёхмерный (а ведь могли бы его нарисовать и двумерные человечки): передняя и задняя грани — в плоскости рисунка, только со сдвигом одна от другой. Горизонтальные рёбра боковых граней — все параллельны направлению «вдаль».

Трёхмерный куб составлен из квадратных граней («двумерных кубов»), которые склеиваются между собой по рёбрам. Четырёхмерный куб будет состоять из трёхмерных «3-граней», то есть обычных кубиков, которые будут склеиваться по двумерным граням.

Рис. 4
Сначала рисуем (по старому рецепту) «обычный» трёхмерный куб — это «передняя» в том, четвёртом, измерении, трёхмерная грань 4-кубика. На рисунке 4 она показана чёрными рёбрами. Потом из каждой вершины этой «передней 3-грани» проводим палочку-ребро в направлении четвёртого измерения (на рисунке — красные): все боковые 3-грани параллельны направлению «в неизвестность». И, наконец, рисуем «заднюю 3-грань» — ещё один кубик, сдвинутый относительно первого (на рисунке — синий). Вот и всё!
Чтобы хвастаться перед одноклассниками, этого уже достаточно. Но чтобы лучше разобраться, что же это нарисовано, ответим ещё на несколько вопросов.
Задача 0. Сколько у 4-куба вершин? Рёбер? Двумерных (квадратных) граней? Трёхмерных (кубических) 3-граней?

Рис. 5
Эту задачу можно решить разными способами. Мы их сейчас обсудим, и решение найдём. Но прежде, чем читать дальше, попробуйте разобраться самостоятельно. Может быть, вы справитесь и сами!

Рис. 6
Обратите внимание, что на рисунке 4 не все 3-грани выглядят как кубики, некоторые — как параллелепипеды, и вовсе не прямоугольные: для примера мы раскрасили одну 3-грань (рис. 5). Это не беда, и в обычном рисунке трёхмерного куба не все грани — квадраты. Но если вас это расстраивает, можно рисовать посимметричнее, чтобы все 3-грани выглядели почти кубами — как на рисунке 6. Кто сколько тут видит кубиков?
Если вы не знаете, как подступиться к четырёхмерному кубику — вот пара задачек-подсказок, чтобы с ним познакомиться.
Задача 1. Сколько двумерных граней соединяет каждое ребро 4-куба? Сколько двумерных граней сходится в каждой вершине? А сколько трёхмерных граней? Выберите любую вершину и найдите все рёбра, 2-грани и 3-грани, которые в ней сходятся.
Задача 2. Выберем какую-нибудь грань четырёхмерного куба. Сколько есть граней, параллельных ей? (То есть лежащих на параллельных плоскостях.) Теперь выберем трёхмерную грань; сколько в 4-кубе 3-граней, параллельных ей?
Задача 3. Найдите на рисунке 4 как можно больше непараллельных 2-граней.

Решение задачи 0.
Первый способ — непосредственное усмотрение истины из нарисованной картинки. В ней ведь всё есть — и вершины, и рёбра, и все грани... Стоит лишь повнимательнее вглядеться. Но, действуя так, легко ошибиться — недосчитать что-нибудь или, наоборот, подсчитать дважды. Поэтому предлагаю другой способ.
Он основан на идее «подсчёт двумя способами», популярной в олимпиадной математике. Например: из трёх сестёр у каждой по 2 котёнка, а у каждого из котят — по 2 хозяйки; сколько всего котят? Можно представить себе, что каждая хозяйка надела на своего котёнка поводок, и сосчитать поводки. Вот и здесь можно считать двумя способами всё подряд — рёбра, грани...
Сначала всё-таки подсчитаем «в лоб» число вершин, вспомнив, как мы рисовали: у квадрата 4 вершины, у трёхмерного куба 8 (ещё 4 на дальней грани), для 4-мерного куба мы каждую из них продублировали. Итого 8 + 8 = 16. Теперь заметим, что из каждой вершины 4-мерного куба торчит 4 ребра — достаточно проверить для ближайшего угла, они все одинаковы. Итого 16∙4 кончиков рёбер. Но у каждого ребра 2 конца, значит, nвершин ∙4=nрёбер 2; nрёбер=16∙4:2=32. Легче ведь так, чем подсчитывать по рисунку?

Теперь — опять глядя на ближайший угол картинки — можно сообразить, что к одному ребру «прикреплено» 3 грани. Две — из нашего старого кубика и ещё одна — уходящая «в неизвестность», в четвёртую сторону. А сколько рёбер у каждой грани, все знают; значит, умножая число рёбер на 3, мы каждую грань сосчитаем 4 раза. Дальше уж досчитайте сами! И не забудьте ещё разобраться с 3-гранями — трёхмерными кубиками, из которых складывается 4-мерный куб.
Если вам не понравился этот способ или всё с ним ясно, но хочется понять, как решать и другие задачи про «четырёхмерье», вот ещё способ — координатный.
На плоскости можно выбрать две оси — вправо и вдаль, например, если эта плоскость горизонтальная, — и записывать положение любой точки двумя числами: (x, y). Вы так делали в школе. Или дома, играя в морской бой, только там одну цифру заменяют буквой. Эти два числа показывают, сколько надо пройти вдоль каждой оси, двигаясь из начала координат, чтобы прийти в нужную точку. Если добавить третью ось — вверх — и третье число z, можно этими тремя числами описывать положение точки во всём трёхмерном пространстве. А в четырёхмерном нужно ещё четвёртое число — назовём его u: оно показывает, на сколько надо сдвинуться в «ту», четвёртую сторону.
Теперь разберёмся с кубиками разных размерностей. Пусть длина стороны кубика равна 1, один из его углов находится в начале координат, а рёбра направлены вдоль координатных осей.
Тогда на плоскости координаты вершин квадратика — (0,0), (0,1), (1,0) и (1,1). А как устроены рёбра, то есть стороны квадрата? У каждого одна координата равна чему-то определённому — или 0, или 1, а другая меняется от 0 до 1, когда мы вдоль ребра идём.

Рис. 7
В трёхмерном пространстве координаты всех вершин такого кубика — тоже нули или единицы; найдите на рисунке 7, например, вершину (0,0,1) или (1,1,0). А рёбра? У каждого ребра какие-то две из трёх координат «закреплены», а третья в одном его конце равна 0 и ползёт от 0 до 1 по мере движения по ребру к другому концу. Так что задать (указать) ребро — это назвать две его «неподвижные» координаты. С гра нями похожая история, но теперь уже две координаты «бегают, как хотят» в пределах от 0 до 1, и только одна закреплена. Например, у передней грани куба на рисунке 7 координата y равна нулю. А у верхней — z=1.
Упражнение 1. а) Скажите, не глядя на картинку: соединены ли ребром куба вершины (0,1,0) и (0,0,1)? б) Каким ребром соединяются грани x=1 и z=0?
В четырёхмерном пространстве у каждой точки 4 координаты, (x,y,z,u). У каждой вершины куба каждая координата равна 0 или 1. У каждого ребра снова может «бегать», изменяться лишь одна координата, а остальные — теперь уже три — закреплены. У грани закреплены 2 координаты, а у 3-грани — всего одна.

Рис. 8
Упражнение 2. Найдите на рисунке 8: а) вершины (1,0,0,1) и (0,1,1,1); б) ребро x=0, z=1, u=1; в) грань y=u=1; г) 3-грань x=0.
Упражнение 3. Какая грань раскрашена на рисунке 5?

Сколько всего вершин? — а столько, сколько разных четвёрок можно составить из цифр 0 и 1! А 3-граней? — столько, сколько есть способов выбрать одну из четырёх координат и дать ей значение 0 или 1, тo есть 4 ∙ 2 = 8. А рёбер сколько? Столько, сколько есть способов убрать одну лишнюю «бегающую» координату, да умножить на число троек из цифр 0 и 1, то есть 4∙(2∙2∙2)=32. Посчитать двумерные грани опять оставляем вам.
Конец решения задачи 0.
Вот ещё задачка, которую можно решить, помня об аналогии с рисованием 3-мерного кубика в двумерье:
Задача 4. У нас получился проволочный кубик. Какие из рёбер нужно нарисовать пунктирными или стереть, если мы хотим, чтобы наш 4-куб был непрозрачным для четырёхмерного наблюдателя?
Подсказка. Для четырёхмерных существ 3-кубик виден целиком, сразу со всех сторон. Так же, как мы из своего трёхмерья сразу целиком видим квадрат.
Задача 5. У трёхмерного кубика — двумерная (плоская) развёртка, то есть выкройка, из которой его можно сложить. Придумайте, как выглядит трёхмерная развёртка четырёхмерного куба.
Решение этой задачи обсудим в следующем номере.
Художник Мария Усеинова.
Ответ к задаче 0
Двумерных граней 24.
Решение задачи 1

В каждом ребре (например, красном на рисунке) сходятся 3 двумерные грани (красная, жёлтая и фиолетовая), в каждой вершине (жирная точка) — 6 (добавляем три сине-зелёные грани). А трёхмерных граней в каждой вершине сходится 4, они «натянуты» на каждые 3 из четырёх выходящих из вершины рёбер. На втором рисунке они разнесены для наглядности; в исходном кубе они касаются двумерными гранями, так что отмеченные красные точки — их общая вершина — сливаются воедино.
Решение задачи 2

Выберем, например, боковую грань 3-кубика с чёрными рёбрами. Ей параллельны ещё одна грань того же 3-куба и две грани «синего». Всего — 4 параллельные грани в каждом направлении. А 3-грань, параллельная данной, одна.
Решение задачи 3
Через каждую вершину проходит ровно одна грань, параллельная данной. Перечислив все грани с данной вершиной (в задаче 1), мы решили и эту задачу.
Решение задачи 4
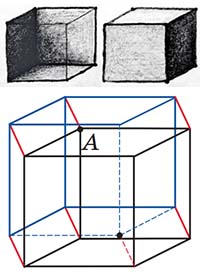
Как устроено изображение трёхмерного куба? У куба есть ближняя поверхность, которую мы видим, и дальняя, скрытая от взора (см. рисунок). Каждая из них состоит из трёх квадратов (на рисунке — параллелограммов), сходящихся в одной вершине (соответственно, ближней или дальней). Также и с 4-кубом: у него (для наблюдателя в 4-мерии) есть ближняя поверхность из всех четырёх кубов (на рисунке — параллелепипедов), сходящихся в одной вершине А, — эту картину мы видели в конце задачи 1 — и дальняя, из четырёх кубов-параллелепипедов у дальней вершины. Чтобы найти невидимые рёбра, нужно выбрать, какая вершина будет дальней (из тех, что во внутренности рисунка), и исходящие из неё 4 ребра будут невидимы.
Ответы к упражнениям 1-3

Упражнение 1. а) Нет, у точек, лежащих на одном ребре, совпадают две из трёх координат; б) Ответ тривиальный — ребром, у которого x=1, z=0, оно параллельно оси y.
Упражнение 2. а) — в) Красная и зелёная точки, фиолетовое ребро и розовая грань на левом рисунке; г) жёлтая грань на правом рисунке.
Упражнение 3. z=1.
Избранное
См. также
























Рис. 1