Пифагор на велосипеде

Григорий Мерзон
«Квантик» №8, 2019

Теорема Пифагора и площадь кольца

Наверняка вы знаете несколько доказательств теоремы Пифагора. Обсудим ещё одно.

Возьмём прямоугольный треугольник и будем вращать его (в плоскости треугольника) вокруг вершины острого угла.

Какую площадь при этом «заметает» треугольник? С одной стороны, ясно, что это просто площадь круга, радиусом которого является гипотенуза, πc².

С другой стороны, этот круг состоит из частей, заметаемых двумя катетами. С одной из этих частей всё понятно: это круг, его площадь равна πa². Осталось доказать, что площадь второй части, кольца, равна πb², и теорема Пифагора доказана:

πa² + πb² = πc²

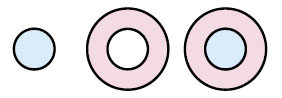
Утверждение про площадь кольца выглядит довольно неожиданно: если увеличивать катет a (не меняя катета b), то, расширяясь, кольцо становится всё тоньше и тоньше — но его площадь не меняется. Вот одно из следствий.

О замечательных следствиях этой задачи мы поговорим в другой раз. А сейчас вернёмся к утверждению про площадь кольца.

Велосипедная теорема Мамикона

Представим себе, что катет b — это... рама велосипеда. Велосипед едет по кругу: его заднее колесо катится без проскальзывания по окружности радиуса a, переднее колесо — по окружности радиуса c.

Оказывается, что нужное нам утверждение о площади кольца — это частный случай следующей замечательной теоремы.

Если велосипед¹ с рамой длины b проехал так, что следы и от переднего, и от заднего колеса образуют замкнутые кривые, то заключённая между ними площадь² не зависит от траектории велосипеда и равна πb².

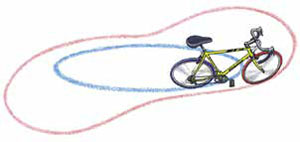
Строгое доказательство этой теоремы потребовало бы использования математического анализа. Но чтобы понять, в чём тут дело, разберёмся со случаем, когда заднее колесо велосипеда движется не по произвольной кривой, а по замкнутой ломаной.

Пока заднее колесо движется по одному из звеньев, переднее тоже движется по прямой; а когда заднее доезжает до конца звена — оно останавливается, а переднее колесо поворачивает по дуге окружности.

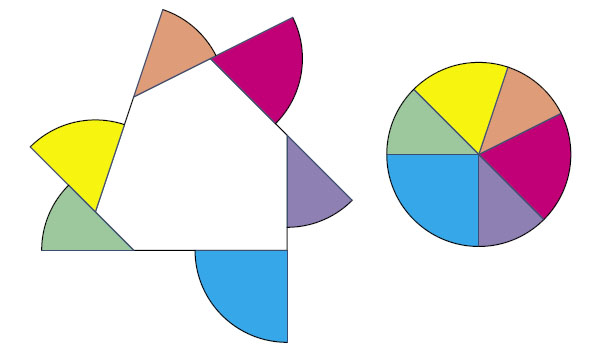
Интересующая нас площадь — это сумма площадей секторов. Радиус каждого из них — длина рамы велосипеда. А так как направление велосипеда делает в итоге полный оборот, заштрихованные секторы складываются в полный круг. То есть интересующая нас площадь действительно равна πb².

В заключение этого доказательства — вопрос. В велосипедной теореме речь шла о движении на плоскости. А что будет, если велосипедист совершил столь большое путешествие, что траекторию уже нельзя считать плоской, а только нарисованной на сфере: будет ли заметаемая рамой площадь по-прежнему равна площади круга радиуса b? Будет больше? Меньше?

Художник Алексей Вайнер

¹ Велосипед должен быть идеально-математическим: мы считаем, что его толщина нулевая, а главное, что он едет без проскальзывания. Последнее означает, в частности, что в каждый момент рама направлена по касательной к траектории заднего колеса.

² Можно для простоты считать, что эти кривые не имеют самопересечений и не пересекаются друг с другом.