Ёлочка с почтовой марки

Николай Авилов
«Квантик» №1, 2018

Почтовые марки — один из предметов коллекционирования. С 1904 года стали выпускаться новогодние марки. Можно собрать целую коллекцию красивых марок с новогодними сюжетами: зимними пейзажами, снеговиками, детьми, катающимися на санках, рождественскими звёздами.

А вот эти марки выпущены в разных странах и в разные годы, но каждая содержит один из главных символов новогодних праздников — ёлочку:

Из представленного набора марок обращаю внимание на новогоднюю ёлочку из Литвы, имеющую строгую геометрическую форму. Наложив на неё квадратную сетку, можно более детально изучить её пропорции и определить размеры ёлочки. Оказалось, что её высота 9 клеточек, основание занимает 10 клеточек. Подсчитайте её площадь (именно такие задания на вычисление площади многоугольников неправильной формы предлагают старшеклассникам на экзамене по математике).

Когда форма и размеры ёлочки заданы, можно сформулировать задачу: разрежьте ёлочку на несколько частей и сложите из них квадрат. Задачи на разрезания многоугольников всегда имеют решение, потому что справедлива теорема Бойяи — Гервина: два многоугольника равной площади являются равносоставленными, то есть один из них можно разрезать на несколько частей, из которых складывается второй многоугольник.

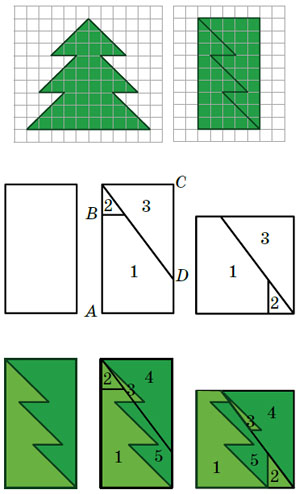
Попробуем и мы. Разрезав ёлочку на две равные части, нетрудно сложить прямоугольник 5×9. Значит площадь ёлочки равна 45 квадратным единицам.

Этот прямоугольник легко перекроить в квадрат, разрезав его лишь на три части (рисунок справа). Здесь отрезки AB и CD равны $\sqrt{45}$ — стороне квадрата, равновеликого прямоугольнику. Убедитесь, что прямоугольник и квадрат равносоставлены, то есть сложены из соответственно равных фигур.

Если совместить эти два разрезания, то получим разрезание ёлочки из почтовой марки на 5 частей такое, что из полученных фигур складывается квадрат. Такое преобразование фигур в квадрат и называется квадрированием.

Задача решена, но возникает естественный вопрос: можно ли эту ёлочку разрезать на меньшее число частей, из которых тоже складывается равновеликий ей квадрат? Оказывается, можно!

Заметим сначала, что и ёлочками, и равновеликими им квадратами можно замостить плоскость:

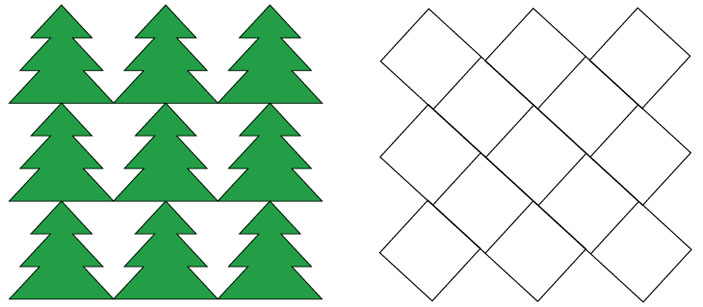
Паркеты мы выбрали довольно хитрые: тут не только полоски квадратов смещены друг относительно друга, но и этажи ёлочек тоже: каждая зелёная ёлочка расположена не ровно над той, что под ней, а со смещением примерно в 1/20 клеточки. Оказывается, если такой паркет из ёлочек нарисовать на бумаге, а паркет из квадратов нарисовать на плёнке и наложить их друг на друга, то можно подобрать такое их расположение относительно друг друга, что ёлочка и квадрат окажутся равносоставленными^*. Равные фигуры раскрашены одним цветом:

Поскольку площади ёлочек и квадратов равны, мы получим разрезание ёлочки на 4 части, из которых складывается квадрат. Выделим отдельно одну ёлочку и один квадрат (рисунок слева).

Напоследок предлагаем поэкспериментировать с квадрированием ёлочек с большим числом «этажей» (у той, которую мы разрезали, этажей всего три).

Художник Алексей Вайнер

^* Попробуйте доказать это самостоятельно. Заметим, что одной картинки не достаточно — на глаз можно не заметить зазоры или наложения.