Гидравлический горизонт событий

В недавней новости рассказывалось о том, что ученым удалось создать лабораторный аналог горизонта событий черной дыры и даже наблюдать аналог хокинговского излучения от него. Оказывается, простейший аналог горизонта событий каждый может обнаружить — и поизучать! — у себя дома. Пустите из водопроводного крана струю воды, по возможности ровную, на дно горизонтальной раковины; подойдет и другая твердая горизонтальная поверхность с бортиками. Вы увидите приблизительно круглую границу, за которой толщина водного слоя резко подскакивает (как на верхнем фото). При подходящих условиях граница может быть близкой к идеальному кругу, а сама поверхность — исключительно ровной, без признаков турбулентности, но эффект легко заметен практически в любых условиях. Обратите внимание, что чем сильнее напор воды, тем больше радиус границы, а если набирать воду в поднос с бортиками, то чем выше уровень набранной воды, тем радиус меньше.

Это — гидравлический скачок (hydraulic jump). Он возникает в результате противоборства двух сил. C одной стороны, перепад высот толкает воду снаружи во внутреннюю область, — и это особенно заметно в емкости с бортиками. С другой стороны, течение воды сносит наружу все попытки продвинуться вовнутрь. Когда вода растекается при ударе струи о поверхность, то сначала радиальная скорость течения очень высока, но потом, по мере удаления от струи, она уменьшается. Это вытекает из закона сохранения потока с учетом того, что толщина слоя изменяется мало. Скачок возникает в том месте, где течение воды уже не может перебороть обратную тенденцию. Похожее явление в более крупных масштабах иногда встречается в устьях рек и носит название приливной бор (см. видео).
Это явление заметил и описал еще Леонардо да Винчи, а первое серьезное математическое описание эффекта опубликовал Лорд Рэлей в 1914 году (On the Theory of Long Waves and Bores). На это явление удобнее всего посмотреть с точки зрения волн на поверхности воды. Скачок высоты — это деформация поверхности, это компактный сгусток волн, и вообще-то эти волны должны разбегаться по поверхности. Они и пытаются это делать, но только скорость течения воды во внутренней области превышает скорость этих волн, поэтому они туда попасть не могут. Можно сказать, что течение воды во внутренней области — «сверхзвуковое»; слово взято в кавычки потому, что сравнивать его надо не с настоящим звуком, а с волнами на поверхности. Еще надо добавить, что у волн на поверхности воды нет какой-то одной постоянной скорости, их скорость зависит от длины волны. Но в наших условиях (тонкий водный слой) зависимость упрощается, и скорость становится почти постоянной. Поэтому и граница получается такой четкой: для разных волн она находится примерно в одном и том же месте.
Переход со «сверхзвукового» на «дозвуковое» течение является гидродинамическим аналогом горизонта событий: никакие возмущения поверхности снаружи области не могут пересечь фронт и проникнуть во внутреннюю. Это ситуация, обратная горизонту событий черной дыры, и ее обычно называют «белой дырой». Аналогия не только на уровне слов и картинок, но и на уровне формул: распространение колебаний по поверхности движущейся жидкости можно переписать в виде волн в пространстве с необычной метрикой. В метрике присутствует сингулярность, которая и сигнализирует о горизонте событий. Так что, хотя пока неизвестно, могут ли существовать ли такие экзотические гравитационные объекты как белые дыры в реальности, но простейший лабораторный аналог — вот он, перед вами.

При внесении возмущения в центральную область наблюдается аналог «сверхзвукового конуса». Фото из статьи G. Jannes, G. Rousseaux, 2012. The circular jump as a hydrodynamic white hole
Есть прямой способ убедиться в том, что внутренняя область действительно движется со «сверхзвуковой» скоростью. Для этого надо внести туда источник волн, воткнув препятствие в поток жидкости, как на фото выше. Поверхность воды, огибая препятствие, деформируется и порождает возмущения, которые расходятся в разные стороны — источник «излучает». Однако из-за сверхзвукового течения эти возмущения уходят не во все стороны, а только в направлении «сверхзвукового конуса». Угол раскрытия конуса зависит от соотношения между скоростью течения воды (или, что то же самое, скоростью источника в системе движения воды) и скоростью распространения волн: чем ближе они друг к другу, тем шире конус. Помещая источник в разные места внутренней области «белой дыры», можно действительно убедиться, что угол раскрытия разный. Любопытно, что статья с подробным описанием этого исследования была опубликована совсем недавно, в 2011 году (Experimental demonstration of the supersonic-subsonic bifurcation in the circular jump: A hydrodynamic white hole, препринт статьи доступен как arXiv:1010.1701; популярное изложение см. в статье The circular jump as a hydrodynamic white hole).
Аналогия между гидравлическим скачком и гравитационным горизонтом событий, как и всякая аналогия, имеет ограниченную применимость. При течении воды может возникать турбулентность, а на форму свободной поверхности влияют капиллярные силы. В результате, как показали недавние эксперименты, круглая форма границы может в подходящих условиях смениться на многоугольник, как это показано на следующем фото. Однако нет оснований ожидать то же самое и для настоящего гравитационного горизонта событий — все-таки исходная физическая система там совсем иная. Впрочем, вопрос о том, бывают ли гравитационные решения уравнений Эйнштейна с турбулентной метрикой, как минимум, имеет право на существование и обсуждение.

Гидравлический скачок в виде многоугольника. Фото из статьи M. Labousse, J. W. M. Bush, 2013. The hydraulic bump: The surface signature of a plunging jet
Фото гидравлического скачка в раковине — с сайта en.wikipedia.org.
-
Что-то я не понял логику в одном месте. Для меня понятно, что скорость воды падает (потому что трение). Но почему априори должно быть понятно, что толщина слоя относително постоянна (из чего у Вас падение скорости выводится) - я не понимаю. У меня по прикидкам получилось h~c/r+kr^2, не сказал бы, что это относительное постоянство по r...
-
Насколько я понимаю, скорость воды падает не из-за трения, а из-за постоянства толщины слоя. А значит, чем выше радиус, тем выше площадь сечения, через которое проходит поток воды. Чтобы один и тот же объем воды за одно и то же время проходил через сечения разной площади, его скорость должна быть разной.
-
Я как раз про то и спрашиваю, с чего толщина слоя постоянна. Я не вижу никакого физического закона, никакой силы, которые бы непосредственно влекли постоянство толщины. Единственный вывод толщины, который я знаю, состоит в подсчёте силы трения, как она влияет на скорость и последующем выводе оттуда уравнения на высоту, а не наоборот. Сила трения есть, о "законе сохранения толщины" не слыхал.
-
-
-
> Но почему априори должно быть понятно, что толщина слоя относително постоянна...
Я такого закона не имел в виду. Я вообще в этом месте все сложности замел под ковер как не слишком существенные, хотя и сложные (и вообще, я даже не смотрел публикации с точным решением в вязком случае или с подробным экспериментальным исследованием). Я лишь сказал, что в целом получается так, что скорость падает, а толщина не уменьшается существенно, но слукавил, создав некорректное ощущение, что является следствием чего.
Как вы правильно сказали, вязкость тут принципиально важна. В случае нулевой вязкости и полного проскальзывания на поверхности (а также считая толщину малой и вдобавок пренебрегая возможным самопроизвольным нарушением осевой симметрии) течение будет с постоянной скоростью и с толщиной, уменьшающейся как 1/r, по закону сохранения энергии. Вязкость диссипирует эту энергию, заставляя воду тормозить, и как следствие, толщина становится больше, чем 1/r.
Но есть и второе последствие — если считать течение в тонкой пленке ламинарным, по крайней мере, без турбулентности по толще, то поток растет с толщиной не линейно, а квадратично. Поэтому как только пленка начнет утоньшаться, поток резко снизится, и сзади, поверх этой пленки, потечет новый слой. То же самое можно увидел через закон дисперсии на мелкой воде. Ну и еще можно вспомнить, как вообще текут тонкие пленки жидкости: при достаточном большом потоке ламинарный режим сменяется волновым, когда избыток жидкости течет по поверхностному слою.
Эти эффекты дополнительно выравнивают толщину слоя. Она конечно не константа, как-то меняется, но в грубом приближении ее можно считать примерно постоянной. И тогда падение скорости можно легко увидеть. Хотя исходной причиной действительно является вязкость.
Было бы не менее интересно вдогонку "гидравлическому" примеру дать, может быть в виде задачи, "гидростатический" пример баланса двух сил - силы поверхностного натяжения и силы земного тяготения в капилляре.
Здесь, кроме известной формулы Жюрена, есть своеобразный аналог архимедова рычага, только не для сил и плеч, а для масс и плеч.
Ваши задачи всегда интересны не только подходами к решениям, но и привязкой к ним новизны.
Последние новости


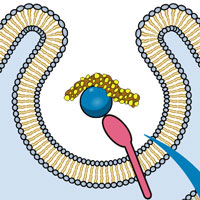

















Гидравлический скачок при растекании силиконового масла по ровной твердой поверхности. Фото из статьи G. Jannes, G. Rousseaux, 2012. The circular jump as a hydrodynamic white hole