Моделирование резких изменений в популяционных процессах

Азиатские медоносные пчелы (Apis cerana) атакуют особь гигантского азиатского шершня (Vespa mandarinia). Фотография Masato Ono с сайта (entnemdept.ufl.edu/creatures/MISC/ BEES/Vespa_mandarinia.html)

В статье рассматривается моделирование биологических процессов, протекающих со скачкообразными изменениями состояний, в частности динамика популяций во время вспышек численности. Особенность авторских моделей состоит в том, что математические исследования ориентированы на описанные в литературе проблемы конкретных биологических ситуаций (вспышки численности листоблошек, коллапс трески у п-ва Лабрадор), что позволяет развивать оригинальный метод для организации модельной вычислительной структуры, поведение которой исследуют с применением фундаментальных теорем нелинейной динамики. Оказалось, что метод организации вычислительной структуры с переключениями и предсказуемыми метаморфозами топологии фазового пространства применим к широкому кругу пороговых явлений в популяционных процессах, которые наблюдаются при стремительной деградации — коллапсе эксплуатируемых запасов.

В работе мы рассматривали моделирование сценариев, относящиеся к области экстремальной динамики биологических процессов. Часто поведение биологических систем меняется достаточно резким образом. Хрестоматийный пример – вспышки численности вредителей, которые повторяются с некоторым интервалом времени. Другая известная ситуация – взрывообразный рост численности вселенца, случайно попавшего и быстро адаптировавшегося в новой среде чужеродного вида. Явление, которое называется «вспышка численности» при ближайшем рассмотрении с математической точки зрения и теории динамических систем (теория хаоса и бифуркаций это один из разделов науки о динамических системах) представляет собой на самом деле группу разнородных процессов. Различаются сценарии развития, что имеет обоснование — новый вид может просто успешно занимать пустующую нишу не вызывая дальнейших изменений в биосистеме. Вселенец может активно уничтожать ограниченные ресурсы кормовой базы, которая не имеет адаптации к новому потребителю. Пример 2020 г. – гигантский азиатский шершень Vespa mandarinia проник в США и способен там уничтожать пчелиные семьи, тогда как пчелы Японии выработали методы борьбы с шершнем (заглавная иллюстрация). В третьем случае агрессивный вид уничтожает свою новую среду обитания. Олени на острове Беринга размножились и вытоптали пастбища. Под последний вариант подходит опасная инфекция в организме с ослабленным иммунитетом, вызывающая летальный сценарий заболевания. Динамика подобных инвазионных процессов развивается по различным сценариям с точки зрения их математической классификации. Все подобные режимы функционирования биосистем являются переходными и экстремальные процессы завершаются за конечное время. Такие явления перетекают в устойчивые состояния или другие режимы, не являющиеся экстремальными. Возможны циклические режимы и осциллирующие вспышки численности в виде серии пиков насекомых. Завершение явлений происходит по внутренним системным причинам, что является проблемой для моделирования. Совсем необязательно вспышку вызывает агрессивный и неуязвимый к естественным врагам вторгшийся вид. Мы рассмотрели данное явление на примере мелких псиллид. Тип вспышки, которые демонстрируют эти насекомые относится к пороговым процессам. Динамика численности резко меняется при достижении пороговых значений. Нам удалось построить математическую модель, которая описывает данный процесс без изменения внутренних параметров. Происходит спонтанное преодоление порога, длительный пик и снова переход к хаотическим колебаниям. Порог создает сложная система регуляторов эффективности воспроизводства, которые мы формализуем убылью на ранних стадиях развития. Численность псиллид во влажных вечнозеленых лесах Австралии регулируют паразиты наездники. Если первичные паразиты активно размножаются, то становятся объектом атак сверхпаразитов и их численность резко снижается. В бореальных лесах поколения насекомых развиваются в разных условиях, потому в таком случае системы должны рассчитываться на разных временных промежутках.

Математическими средствами в сценариях мы вызывали трансформации разных типов аттракторов — замкнутых инвариантных областей (в математике особо устойчивые точки или множества, притягивающие к себе траектории в [фазовом] пространстве). Однако, притяжение траектории к одному из альтернативных аттракторов зависит от формы границ их областей притяжения. Границы могут быть сложно составленными и путь траектории будет непрост.

Рис 1. Вычислительный модельный сценарий с двумя близкими пиками.

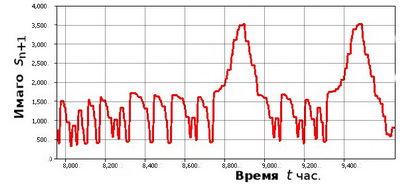
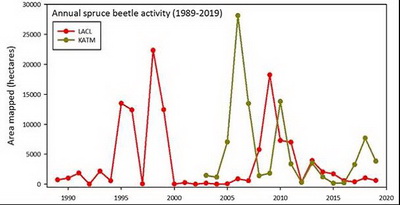
Для этой задачи нам пришлось описать динамику поколений по стадиям развития насекомых и получить сложные дискретные зависимости из решения разрывных дифференциальных уравнений. Для описания явлений мы используем динамику итераций — системы с дискретным временем, где исходная точка отображается некоторой функцией «оператором эволюции» и множество точек во времени называется траекторией. Такая траектория может сходится к устойчивому равновесию или образовывать периодически повторяющиеся перестановки — циклы. В некоторых интересных случаях предельное множество траекторий функциональных итераций оказывается гораздо более сложным, чем цикл из набора точек с конечным периодом - нигде не плотным множеством, и говорят, что траектория из начальной точки притягивается к объекту «странный аттрактор». Траектория может уходить в бесконечность — это значит, что динамика не будет диссипативной. Аттракторов может быть несколько, тогда будут важны границы их областей притяжения. Точки границы никуда не притягиваются, и граница областей притяжения может стать аналогично «странной». Внутреннее время наших моделей — непрерывное на фиксированном наборе интервалов. Примененная в разработанном методе структура называется гибридным кадрированным временем, где вычисляемые события посреди непрерывного интервала вызывают переопределения в форме правых частей уравнений. Что бы правильно рассчитать моменты событий необходимы дополнительные факторы и вспомогательные уравнения системы. Специальный функционал реагирует на численность популяции и увеличивает смертность на второй стадии развития, что разрушает аттрактор итераций – вспышка заканчивается и популяция переходит в режим хаотических малочисленных колебаний. Данному режиму будет отвечать фрактальный репеллер — несвязное континуальное множество не притягивающихся к аттракторам точек. Система в хаотическом режиме имеет вероятностный характер поведения, потому чаще всего скоро следует повторный пик вспышки численности вредителя (рис. 1). Подобная ситуация наблюдается в случае вспышек вредителя жука лубоеда Dendroctonus rufipennis в Аляске и США (рис. 2). На графиках вспышек показывается площадь пораженного леса, тут 0 не означает вымирание популяции насекомых. Скорое повторное преодоление порога достаточно вероятное событие, так численность сверх паразитов достаточно велика, и насекомые за одну вспышку не могут уничтожить полностью лес.

Рис 2. Динамика серии пиков численности елового лубоеда Dendroctonus rufipennis в лесах Аляски.

Вспышка численности в модели не требует внешних факторов для запуска и нет необходимости в искусственном описании ее затухания. В гибридной модели можно реализовать сценарий не вынужденной деградации чрезмерно агрессивной популяции при полном истощении ресурсов среды. Примененные в вычислительных сценарных экспериментах средства инструментальной среды позволяют нам конструировать необходимые метаморфозы и аттракторов и сдвиги границ их областей притяжения, которые могут получать фрактальную структуру.

Серия наших статей о моделях эксплуатируемых популяций рыб и вспышках насекомых относится к такому популярному научному направлению как моделирование биологических процессов. Работы по построению моделей можно разделить на два больших крыла математическую биологию и биологическую математику. Работы этих двух групп пишутся на разном научном языке и используют различный математический аппарат. Наши исследования относятся к редкому промежуточному звену (переходной форме) и ориентированы на описанные в литературе проблемы конкретных биологических ситуаций, что позволяет нам развивать оригинальный метод для организации модельной вычислительной структуры, поведение которой мы исследуем с применением фундаментальных теорем нелинейной динамики.

Рис 3. Динамика коллапса популяции каспийских тюленей Pusa caspica (пунктиром показана динамика половозрелой части популяции)

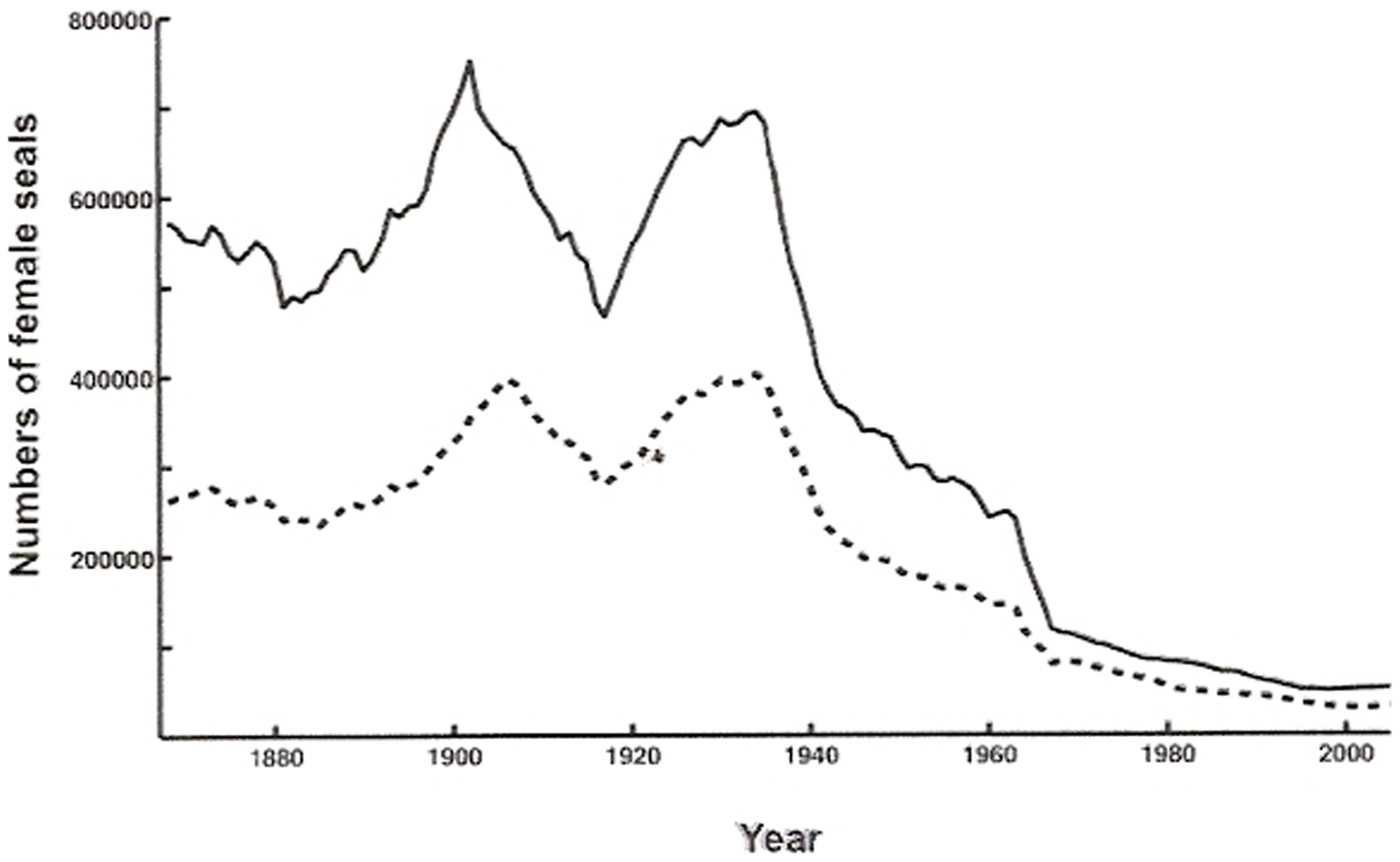
Оказалось, что метод организации вычислительной структуры с переключениями и предсказуемыми метаморфозами топологии фазового пространства применим к широкому кругу пороговых явлений в популяционных процессах, которые наблюдаются при стремительной деградации — коллапсе эксплуатируемых запасов. Сценарий реализуется при незначительном превышении оптимального уровня изъятия из популяции — как в случае Каспийских тюленей. Численность большой промысловой популяции Pusa caspica резко сократилась в 1950 годы и более не восстанавливалась несмотря на все ограничения (рис. 3).

В модели сценарий коллапса выражается эффектом, когда странный аттрактор резко соприкасается с границей своей области притяжения, и более не существует в системе альтернативных равновесных состояний. Подобному быстрому сценарию коллапса без восстановления подвержены запасы крупных долгоживущих объектов промысла таких, как камчатский краб, палтус и треска Атлантики.