Нужна ли физикам теория категорий?

Теория категорий — один из самых абстрактных разделов математики, занимающийся математическими структурами и связями между ними (изображение с сайта haskell.org)

Математик из Оксфордского университета Боб Коуке утверждает, что один из самых абстрактных разделов математики — теория категорий — может оказаться наиболее удобным «языком» квантовой механики.

Таково уж свойство нашего мира, что физические явления эффективнее всего описываются с помощью математики. Математических методов в физике придумано множество — от простых приемов при решении конкретных уравнений до использования теории групп или привлечения еще более сложных объектов.

Но насколько далеко в область абстрактного полезно заглядывать физике? Найдется ли место в теоретической физике, например, такому абстрактному разделу математики, как теория категорий, которую даже сами математики иногда называют «абстрактной чепухой»?

Недавно в архиве е-принтов появилось эссе Боба Коуке (Bob Coecke), сотрудника Вычислительной лаборатории Оксфордского университета, озаглавленное «Введение в теорию категорий для практикующего физика» (Introducing categories to the practicing physicist). В нём автор защищает точку зрения, которая наверняка удивит многих физиков. Он считает, что физикам-теоретикам просто необходимо знать и уметь применять теорию категорий, поскольку они и так работают с категориями (в математически строгом смысле слова), сами того не подозревая!

Что удивительного в этом утверждении? Дело в том, что когда физик-теоретик пишет свои формулы, он всё же держит в голове ту реальную природную систему, с которой он пытается разобраться. А теория категорий — это настолько абстрактная область математики, что поначалу даже непонятно, к чему вообще в нашем мире может относиться эта теория.

Тут стоит пояснить, что хотя математика и тяготеет к изучению абстрактных объектов, уровень абстракции может быть очень разный. Самая простая абстракция — это переход от «двух яблок», «двух камней» и т. д. к понятию числа 2; переход от «я повернулся боком», «камень повернулся боком» к понятию поворота на 90°. При этом манипулирование предметами заменяется на универсальные законы работы с числами (или с преобразованиями, или с чем-то еще).

Абстракция следующего уровня возникает, когда понимаешь, что правила обращения с числами 2, 3, 15 и т. д. по сути одинаковы. Все эти числа можно складывать, перемножать, для них работают переместительный, сочетательный и другие законы. Иными словами, все целые числа «играют по одним правилам». Поэтому часто полезно оперировать не с конкретными числами, а с новым математическим объектом — кольцом целых чисел. Аналогично, разные повороты предмета в пространстве являются элементами нового математического объекта — группы трехмерных вращений.

Третий уровень абстракции — это когда исчезает «осязаемость» элементов групп, колец, полей. Тут уже рассматриваются не конкретные группы вращений или иных преобразований, а просто абстрактные группы — совокупности элементов со строго очерченными свойствами. Здесь на первый план выходит то, какова структура группы, а не то, из чего она «состоит». Свойства всевозможных непротиворечивых математических структур, безотносительно к тому, где именно эти структуры возникают, изучает абстрактная алгебра.

Теория категорий предлагает подняться еще выше, на четвертый уровень абстракции. В ней изучаются уже не конкретные группы, а сеть математических взаимосвязей между разными группами. Аналогично, изучается сеть взаимосвязей между самыми разными типами пространств или между самыми разными кольцами. Более того, оказывается, что эти сети взаимосвязей (групп, полей, пространств и т. д.) — очень шаблонны. Между ними (между сетями!) можно установить параллели, и с помощью этих параллелей высокого уровня иногда удается решить очень трудные, но вполне конкретные задачи.

Автор эссе утверждает, что именно «опыт распознавания структур», который уже накопила теория категорий, будет очень полезен физикам-теоретикам. В качестве конкретного примера он берет такой раздел физики, как квантовая механика, и постепенно облекает ее в категорную форму. Оказывается, многие ключевые для квантовой механики понятия, например принцип суперпозиции (благодаря которому возможны запутанные состояния), локальность, причинность и т. д., возникают в подходящих категориях сами собой. В них даже находятся готовые аналоги для не до конца понятого процесса измерения квантовой системы.

Разработанный авторами «картиночный формализм» позволяет эффективно доказывать утверждения в квантовой механике, не прибегая к длинным формулам (изображение из статьи B. Coecke, Kindergarten Quantum Mechanics)

В чем польза от такой переформулировки квантовой теории? Раз квантовая механика точь-в-точь вписывается в «трафарет» теории категорий, то значит сеть взаимосвязей между квантовыми объектами можно как бы увидеть «с высоты птичьего полета», не прибегая к конкретным вычислениям. И тогда некоторые нетривиальные результаты квантовой теории (например, теорема о невозможности клонирования квантового состояния, квантовая телепортация и т. п.) становятся очень естественными в категорной формулировке.

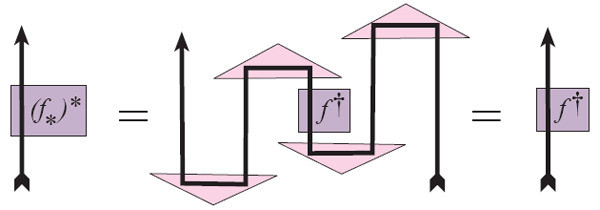
Мощь теории категорий можно поставить «на конвейер» и использовать в рутинных вычислениях. Несколько лет назад Боб Коуке с коллегами на основе теории категорий разработал простой «картиночный формализм», заменяющий собой формульные вычисления в квантовой теории информации. Этот формализм является, по сути, двумерной версией формализма бра- и кет-векторов, созданного на заре квантовой механики Полем Дираком. Чтобы подчеркнуть, насколько простыми становятся вычисления в этом подходе, автор назвал одну из своих статей «Детсадовская квантовая механика» (Kindergarten Quantum Mechanics).

Автор эссе в заключении говорит, что категории являются мощным и гибким «шаблоном», с уже готовыми конструкциями и теоремами, по которому можно строить самые разные физические теории, а не только квантовую теорию информации. Возможно, с их помощью будут открыты новые глубокие связи между уже существующими теориями. Поэтому он призывает к тому, чтобы включать курс теории категорий в университетские программы не только математиков, но и физиков и даже информатиков.

Источник: B. Coecke. Introducing categories to the practicing physicist // препринт arXiv:0808.1032 (7 August 2008).

См. также:
1) S. Abramsky, B. Coecke. Categorical quantum mechanics // препринт arXiv:0808.1023 — глава в книге «Handbook of Quantum Logic and Quantum Structures», vol. II, Elsevier, 2008.
2) B. Coecke. Kindergarten Quantum Mechanics // препринт quant-ph/0510032 — лекции, прочитанные на различных конференциях и школах.
3) A. Doering, Ch. Isham. 'What is a Thing?': Topos Theory in the Foundations of Physics // препринт arXiv:0803.0417 — еще один, не менее абстрактный подход к построению физических теорий.

Игорь Иванов