Стандартная модель выдержала еще одну проверку

Через 30 лет после создания Стандартной модели удалось наконец экспериментально доказать «бегучесть» угла Вайнберга.

Среди многочисленных предсказаний Стандартной модели — краеугольного камня физики элементарных частиц — есть и предсказание о том, что фундаментальные константы теории не совсем постоянны, а зависят от того, с какой стороны на них посмотреть, в каком именно эксперименте их измерить. Например, если мы хотим измерить силу Кулона между двумя электронами и выяснить таким образом заряд электрона, то результат будет зависеть от того, на каком именно расстоянии находятся эти электроны. Оказывается, чем ближе друг к другу электроны, тем большим «выглядит» их заряд (правда, эту зависимость можно заметить лишь на субатомных расстояниях). Такое поведение — зависимость характеристик частицы от того, с какого расстояния мы на нее смотрим, — называется бегучесть констант.

В зависимости от расстояния до частицы «бежит» не только ее электрический заряд, но и «сильный» заряд, т. е. источник сильного взаимодействия между частицами. «Бегучесть» обоих этих зарядов хорошо изучена экспериментально и прекрасно согласуется с теоретическими расчетами в рамках Стандартной модели. Теория также предсказывает, что «бежать» должна и величина, характеризующая слабое взаимодействие, — так называемый угол Вайнберга.

Однако экспериментально подтвердить это предсказание оказалось непросто. Слабое взаимодействие полностью оправдывает свое название: оно гораздо слабее сильного и электромагнитного, и для того, чтобы «извлечь» проявление слабого взаимодействия из эксперимента, приходится вылавливать чрезвычайно слабые изменения наблюдаемых величин. За всю историю Стандартной модели (а ей уже за тридцать лет!) существовало всего одно по-настоящему точное измерение угла Вайнберга — на очень малых расстояниях, которые отвечают очень высоким энергиям (а конкретно — энергии рождения Z-бозона, нейтрального переносчика слабого взаимодействия). А по одной точке, разумеется, невозможно определить, изменяется ли функция или остается постоянной.

За прошедшие годы делались неоднократные попытки измерить угол Вайнберга и при низких энергиях, однако точность этих измерений всегда была очень мала. И лишь недавно, 26 апреля 2005 года, появился препринт [1] экспериментальной группы, работающей на Стэнфордском линейном коллайдере (эксперимент SLAC E158), в котором сообщается, что угол Вайнберга измерен при очень малых энергиях с достаточной точностью.

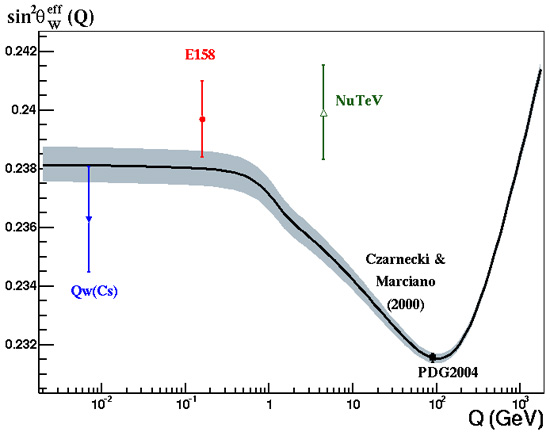
В течение 2002-2003 годов эта группа изучала рассеяние поляризованных электронов на неполяризованных атомах со средним импульсом отдачи около 160 МэВ (мегаэлектронвольт) и измеряла зарядовую асимметрию — различие между рассеянием право- и левопоряризованных электронов. Чтобы подчеркнуть филигранность эксперимента, заметим, что сечение рассеяния приходилось измерять с относительной точностью в миллиардные доли! Только на таком уровне точности становились заметны проявления слабого взаимодействия.

Результат эксперимента составил:

sin²(θ_W) = 0,2397 +/– 0,0010 (статистическая погрешность) +/–
+/– 0,0008 (систематическая погрешность),

что в пределах погрешности совпадает с теоретическим предсказанием и отличается от значения, измеренного на Z-пике, на 6,2 стандартных отклонений. Вероятность случайного отклонения на такую большую величину столь ничтожна, что бегучесть угла Вайнберга (наконец-то!) можно считать экспериментально доказанной. Кроме того, этот эксперимент, по-видимому, поставил точку в трехлетнем споре, порожденном загадочными результатами эксперимента NuTeV (тогда казалось, что при низких энергиях значения угла Вайнберга отличаются от расчетов Стандартной модели; см. [2]). Таким образом, Стандартная выдержала прошла еще одну проверку.

Более того, результат эксперимента не просто подтверждает Стандартную модель, считают авторы статьи, но и дает ограничения на ряд экзотических теоретических конструкций, которые можно было бы построить «поверх» Стандартной модели.

См. также:
[1] P. L. Anthony et al, SLAC E158 Coll., "Precision measurement of the weak mixing angle in Moller scattering", e-print hep-ex/0504049, статья должна в скором времени появиться в журнале Phys. Rev. Lett..
[2] Проблемы с углом Вайнберга в эксперименте NuTeV — страница из проекта «Текущие открытия в физике элементарных частиц (ФЭЧ)».
[3] Аномальный магнитный момент мюона: физика за пределами Стандартной модели? — заметка о том, как и зачем проверяют Стандартную модель.
[4] Физика ядра и частиц, XX век — веб-версия учебного пособия НИИЯФ МГУ.

Игорь Иванов