Эллипс, гипербола и парабола

Федор Нилов
«Квантик» №2, 2023

В этой статье мы познакомимся с эллипсом, гиперболой и параболой. Посмотрим, чем они похожи, а чем отличаются.

Рис. 1. Бифокальное определение эллипса: MF₁ + MF₂ постоянно

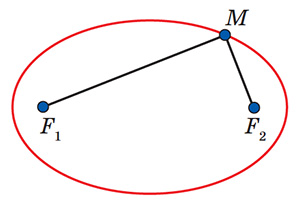
Мы хорошо знаем, что все точки окружности находятся на одинаковом расстоянии от её центра. Эллипс, который можно представлять себе как сплющенную окружность, обладает похожим свойством. Внутри эллипса есть две точки, которые называются его фокусами: сумма расстояний от них до любой точки эллипса одна и та же (рис. 1). Иначе говоря, если привязать нерастяжимую верёвку к двум колышкам и прикрепить ошейник козы к этой верёвке, то коза сможет дотянуться до травы на лужайке, граница которой — эллипс. Если фокусы у эллипса совпадают, он превращается в окружность.

Рис. 2. Бифокальное определение гиперболы: |MF₁ — MF₂| постоянно

У гиперболы тоже есть два фокуса, но для всех её точек постоянна разность расстояний до фокусов (из большего вычитаем меньшее). Таким образом, гипербола состоит из двух ветвей: если расстояние до одного фокуса больше, точка лежит на одной ветви, иначе — на другой (рис. 2).

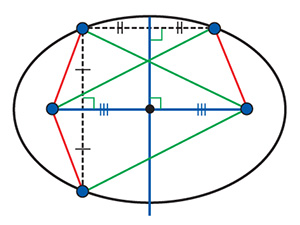
Рис. 3

Покажем, что эллипс и гипербола — симметричные фигуры. Отразим точку, лежащую на эллипсе, относительно прямой, проходящей через его фокусы (рис. 3).

Рис. 4

Расстояния до фокусов не изменятся, поэтому сохранится и их сумма. Значит, отражённая точка тоже лежит на эллипсе, а прямая, проходящая через фокусы, — это ось симметрии эллипса. Вторая ось симметрии — серединный перпендикуляр к отрезку, соединяющему фокусы. При симметрии относительно этой оси расстояния до фокусов меняются местами.

Гипербола также имеет две оси симметрии: одна проходит через фокусы, а другая является серединным перпендикуляром к отрезку, соединяющему фокусы (рис. 4).

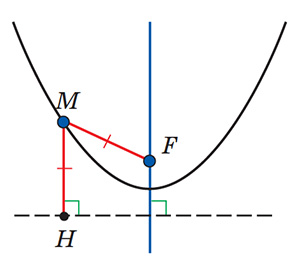
Рис. 5

У эллипса и гиперболы есть и центр симметрии — середина отрезка, соединяющего фокусы.

Парабола образована всеми точками плоскости, расстояние от которых до фиксированной точки (фокуса) равно расстоянию до фиксированной прямой (директрисы)¹. Парабола имеет лишь одну ось симметрии, она проходит через фокус и перпендикулярна директрисе (рис. 5).

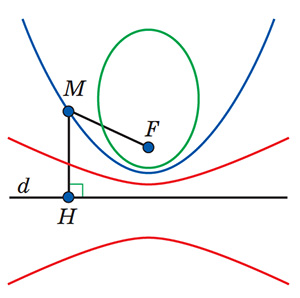
Рис. 6. Фокально-директориальное определение эллипса, гиперболы и параболы, MF : MH = ε

Определение параболы заметно отличается от определений эллипса и гиперболы. Оказывается, для всех трёх кривых можно дать одно общее определение. Зафиксируем прямую d (она будет директрисой) и не лежащую на ней точку F (это будет фокус), а затем выберем любое положительное число ε, которое назовём эксцентриситетом. Рассмотрим все точки M, для которых отношение расстояния до фокуса к расстоянию до директрисы равно ε. Если ε < 1, получится эллипс, если ε > 1 — гипербола, а если ε = 1 — парабола (зелёная, красная и синяя фигуры на рисунке 6).

Оказывается, для каждого из двух фокусов гиперболы и эллипса есть своя директриса, а фокусы в  бифокальном и фокально-директориальном определениях — это одни и те же точки (рис. 7).

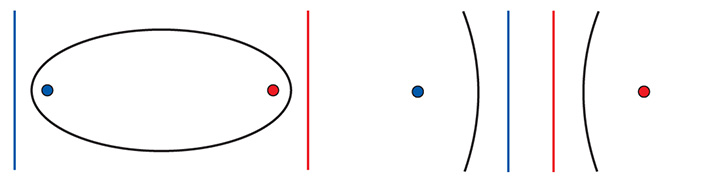
Рис. 7

Рис. 8

Если эксцентриситет ε близок к нулю, эллипс становится похож на окружность. Если ε очень большой, ветви гиперболы становятся похожими на директрисы.

Эллипсы, гиперболы и параболы называют одним общим термином: кониками или коническими сечениями, поскольку каждая из этих кривых может быть получена как сечение конуса плоскостью² (рис. 8). По-видимому, этот факт впервые обнаружил древнегреческий математик Менехм в IV веке до н. э., а первое сохранившееся доказательство появилось в монографии «Конические сечения» Аполлония Пергского в III веке до н. э.³

Коники зачастую встречаются в окружающей жизни. Верхний край кружки выглядит как эллипс, если на неё посмотреть под углом. Струи фонтана имеют форму параболы. След фонаря на тёмной поверхности — коника (это как раз сечение светового конуса). Большинство небесных тел Солнечной системы, согласно закону Кеплера, вращаются по эллипсам с фокусом в Солнце. Некоторые кометы летят по параболам и ветвям гипербол.

Кстати, сечение цилиндра наклонной плоскостью (другими словами, срез колбасы) — тоже эллипс.

В следующем номере мы обсудим, почему сечения конуса являются эллипсами, гиперболами и параболами, поймём, где находятся их фокусы и директрисы, а также рассмотрим различные обобщения.

¹ См. также статью Д. Русаковой в №12 за 2015 год.

² Об этом «Квантик» писал в №8 за 2013 год.

³ См. книгу «Аполлоний Пергский».

Художник Мария Усеинова