Парадокс Бертрана

Амелия Алаева
«Квантик» №6, 2022

Однажды Маша, листая ленту соцсетей, наткнулась на интересную задачу: «Дана окружность, в которую вписан равносторонний треугольник. Какова вероятность того, что случайно выбранная хорда окажется больше его стороны?» Она открыла раздел с  комментариями, и там мнения сильно разнились, но в основном пользователи разделились на три непримиримых лагеря. Маша решила положить конец спорам и решить задачу самостоятельно.

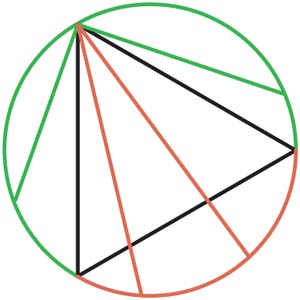
— Так... А если выбрать хорду в произвольном месте, а потом её переместить? — по привычке начала рассуждать вслух Маша. — Переместим, значит, её так, чтобы один из концов хорды совпал с вершиной треугольника. При этом окружность разбита на 3 равные дуги (треугольник-то равносторонний!). Если конец хорды будет лежать на этих, допустим зелёных, дугах, то хорда окажется меньше стороны. А если на красной, то больше (рис. 1). Значит, вероятность равна 1/3. Что тут думать-то?

Маша случайно взглянула на часы: секундная и минутная стрелки почти одинаковой длины. А если представить, что так оно и есть, то она пару секунд назад получила ответ на вопрос, с какой вероятностью расстояние между концами стрелок окажется больше, чем радиус циферблата. Удивительно!

Но на этом она не остановилась. Как известно, многие геометрические задачи имеют не одно решение. Она хотела найти здесь ещё что-нибудь интересное. И нашла! Но, на удивление, новый подход привёл её к другому ответу:

— Хм... А можно же использовать радиус окружности и выбирать хорду относительно него! Пусть у нас есть зафиксированный радиус, который перпендикулярен стороне треугольника. Тогда выберем любую точку на этом радиусе и проведём через неё хорду, параллельную стороне. Если эта хорда «выше» неё, то она больше, если же «ниже», то меньше! Но как нам посчитать вероятность? Ага, сторона делит радиус на 2 равные части, следовательно, шанс выбрать точку из большей хорды равен 1/2.

Итак, у меня получилось два разных ответа: 1/3 и 1/2. Но какой же из них верный? Да, я как раз читала об этом споре в комментариях... Вроде бы ошибки ни в первом, ни во втором рассуждении я не вижу...

Когда сил думать больше не осталось, Маша пошла просить помощи у соседа Ивана Петровича, который по счастливой случайности был профессором в  области теории вероятностей и статистики. Кто, если не он, по-настоящему умный человек, сможет разгадать эту загадку?

— На самом деле, оба решения верны и вполне себе возможны, — выслушав Машу, согласился Иван Петрович. — Хм, эта задача называется парадоксом Бертрана. Его суть заключается в том, что невозможно подсчитать вероятность, не договорившись о выборе случайной величины.

— Ого, то есть такое противоречие не только у меня получилось!

— Действительно. Впервые сам Жозеф Бертран описал эту идею именно на таком примере. Ты нашла два из трёх предложенных им решений. Они называются «метод случайных концов» и «метод случайного радиуса», а есть ещё и «метод случайного центра».

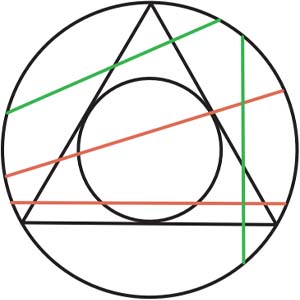
Выберем произвольную точку внутри круга и построим хорду с центром в этой точке. Оказывается, хорда будет длиннее стороны треугольника, только если выбранная точка находится внутри окружности, вписанной в равносторонний треугольник. Как известно, отношение площадей вписанной окружности к описанной для равностороннего треугольника составляет 1/4, откуда и соответствующая вероятность.

— Ничего себе! Три разных результата! Но для первого случая я пример со стрелками часов найти смогла, поэтому он, наверное, самый реальный, то есть «самый правильный»?

— Тут-то и кроется смысл парадокса: все три решения по-своему правильные! А задачки для каждого из них придумать можно. Вот, к примеру, весь мой кофейный столик заляпан отпечатками от любимой кружки. Мда, нехорошо...

Маша засмеялась.

— Так вот, один круглый отпечаток пересекает другой в двух точках — вот тебе и случайная хорда. Или моя кухонная доска: прямые царапины от ножа — отрезки, а круг можно «начертить» ещё одним отпечатком стакана. Предлагаю тебе подумать на досуге:

— Хм, аналогия безусловно интересная, но... Иван Петрович, вы не до конца ответили на мой вопрос.

— Ах, да. Все рассуждения верные, но каждое — для своего метода выбора хорды (плотность распределения хорд внутри круга у каждого метода своя). Задача будет иметь чётко определённый ответ только в том случае, если этот метод нам задан. Иногда этот метод можно вывести из общих соображений. Например, американский физик Эдвин Джейнс предложил считать, что если нам не заданы размеры и положение круга, то используемое распределение хорд должно быть к ним безразлично. В таком случае единственным подходящим будет метод «случайного радиуса».

С парадоксом Бертрана сталкиваются каждый раз, когда собирают статистику. Например, какова средняя длина рыбы в пруду? Чтобы это понять, мы можем ловить случайную рыбу, измерять её (и отпускать) и, сделав так много раз, найти среднее. А можем пометить случайных мальков, следить за ними всю их жизнь, регулярно их измеряя, вычислить среднюю длину каждой помеченной рыбы, а потом взять среднее для всех этих рыб. В первом случае средняя длина будет больше, потому что подавляющее большинство рыб не доживает до зрелого возраста. Тем самым ответ зависит от метода определения случайной рыбы аналогично парадоксу о случайной хорде.

Вопрос «Как правильно определить равновероятные исходы в конкретной задаче?» до сих пор волнует многих учёных. Поэтому парадокс Бертрана на практике очень часто всплывает в современной науке при планировании экспериментов и построении математических моделей. Всякий раз, когда требуются случайные величины, важно чётко понимать, какое влияние окажет способ их получения на результаты. Ведь в наше время теория вероятностей и статистика используются везде: в медицине, экономике, психологии и т. п.

— Да, как всё в мире удивительно! Началось всё с поста в Интернете, а закончилось разговором о том, что не всем исследованиям можно доверять.

— Нужно быть любопытным и почаще присматриваться к обычным вещам, тогда узнаешь много всего интересного, — улыбнулся профессор.

Художник Алексей Вайнер