Окружности Карлейля, или Как решать квадратные уравнения циркулем и линейкой
Константин Кноп
«Квант» №7, 2020

Казалось бы, какая может быть связь между квадратными уравнениями и геометрическими инструментами — циркулем и линейкой? Однако эта связь есть, и ее исследование с разных сторон — увлекательнейшая задача, тесно связанная и с геометрией, и с алгеброй.
А при чем тут Томас Карлейль? Согласно Википедии, это британский писатель, публицист, историк и философ, автор многотомных сочинений «Французская революция» (1837), «Герои, почитание героев и героическое в истории» (1841), «История жизни Фридриха II Прусского» (1858–1865). О его занятиях математикой практически ничего не известно, и тем не менее, в честь него назван класс окружностей, помогающих решать квадратные уравнения.
А теперь — обо всем по порядку.
Что мы подразумеваем под решением уравнений циркулем и линейкой?
В школьных учебниках геометрии есть какие-то упоминания о возможности построения квадратичных иррациональностей с помощью геометрических инструментов, но в основном не в виде практических алгоритмов построения, а в качестве теоремы существования. Единственный школьный пример конкретного алгоритма, как-то связанного с квадратными уравнениями, — построение среднего геометрического. Давайте и мы тоже начнем с этой задачи.
Задача 1. Даны отрезки \(a\) и \(b\). Постройте отрезок, равный \(\sqrt{ab}\).
Решение. Отложим на одной прямой \(AD = a\), \(DB = b\). Построим окружность на отрезке \(AB\) как на диаметре. Восставим к нему перпендикуляр в точке \(D\) — в пересечении получим точку \(C\) (рис. 1). Тогда \(CD=\sqrt{ab}\). (Доказательство: угол \(ACB\), опирающийся на диаметр окружности, является прямым. Поэтому треугольник \(ACB\) подобен (по углам) каждому из треугольников \(ADC\) и \(CDB\), откуда \(AD:CD=CD:DB\), и \(ab=AD\cdot DB=CD^2\).)

Рис. 1. Построение среднего геометрического
Обычно после решения этой задачи в школе говорится, что поскольку мы умеем с помощью циркуля и линейки складывать, вычитать, также умножать и делить (пользуясь теоремой Фалеса), а вот теперь умеем и корни извлекать, то этого уже достаточно для того, чтобы по формулам для корней квадратного уравнения научиться строить отрезки соответствующей длины. Действительно, достаточно. Но ведь дико неудобно!
К счастью, есть и нормальный способ «геометрического» решения квадратных уравнений, известный вот уже более двух веков. Этот способ впервые был описан шотландским математиком и физиком Джоном Лесли в его книге «Элементы геометрии и плоской тригонометрии», изданной в 1809 году. В одном из последующих изданий Лесли добавил сноску о том, что идея этого способа принадлежит его бывшему ученику Томасу Карлейлю.

Рис. 2. Задача Лесли, страница из его книги
На рисунке 2, заимствованном из книги Лесли, сформулирована задача: «Построить прямоугольник, равновеликий данному прямоугольнику \(CDFE\), полупериметр которого равен данному отрезку \(BC\)». Ее решение, предложенное Карлейлем, показано на рисунке 3. Прокомментируем построение на этом рисунке. Вначале данный отрезок \(BC\) откладывается на продолжении меньшей стороны четырехугольника \((CE)\). Затем на большей его стороне откладывается \(CG=CE\), после чего с помощью параллельных прямых достраивается четвертая вершина прямоугольника \(ABCG\). Теперь достаточно построить окружность на диаметре \(AD\) — точки \(J\) и \(K\) ее пересечения с отрезком \(BC\) и дадут искомые стороны прямоугольника (\(BJ\) и \(JC\) или, как изображено на рисунке, \(BK\) и \(KC=KI\)).

Рис. 3. Задача Лесли в Википедии
Почему и как это работает? Проще всего ответить на этот вопрос с помощью системы координат. Поместим начало координат в точку \(C\), ось абсцисс направим влево (к \(B\)), а ось ординат вверх (к \(D\)). Кроме того, будем считать, что \(CE=e\), \(CB=b\), \(CD=d\). Тогда координатами точки \(A\) будут \((b;\ e)\), а значит, координатами \(M\) будут \((b/2;\ (d+e)/2)\). Это означает, что окружность с центром \(M\) и радиусом \(MG\ (=MA=MD)\) имеет уравнение
\[\left(x-\frac b2\right)^2+\left(y-\frac{d+e}{2}\right)^2=\left(\frac b2\right)^2+\left(\frac{d-e}{2}\right)^2,\]откуда
\[x^2-bx+\left(\frac b2\right)^2+y^2-(d+e)y+\left(\frac {d+e}2\right)^2=\left(\frac b2\right)^2+\left(\frac{d-e}{2}\right)^2\]и
\[x^2-bx+y^2-(d+e)y+de=0.\]Теперь уже совсем нетрудно увидеть, что точки пересечения этой окружности с горизонтальной прямой \(BC\) (осью абсцисс) — это точки, для которых \(y=0\), а значит, они удовлетворяют уравнению
\[x^2-bx+de=0.\]Как мы знаем из школьной алгебры (теорема Виета), сумма корней этого уравнения равна \(b\), а произведение равно \(de\). Таким образом, если \(K\ (x_1;\ 0)\) и \(J\ (x_2;\ 0)\), то \(CK=CJ=x_1+x_2=b=CB\), а \(CK\cdot CJ=x_1\cdot x_2=de\), т. е. площадь прямоугольника со сторонами \(CK\) и \(BK=CJ\) действительно равна площади исходного прямоугольника \(CDFE\).
То же самое можно было получить и не выписывая уравнения окружности, из чисто геометрических соображений. Ведь \(CK\cdot CJ\) — это произведение длины секущей на ее внешнюю часть, a \(de=CD\cdot CG\) — другое такое же произведение. По теореме о секущих, они равны, т. е. \(CK\cdot CJ=de\). А так как \(ABCD\) — прямоугольная трапеция, а \(M\) — середина ее боковой стороны, то высота в равнобедренном треугольнике \(MJK\) является одновременно средней линией трапеции и медианой в том же треугольнике. Отсюда сразу получаем, что \(CK=BJ\), а значит, \(CK+CJ=CB=b\).
Осмысление того, что способ Карлейля годится не только для одной этой задачи, пришло далеко не сразу. Сначала в 1867 году австрийский железнодорожный инженер Эдуард Лиль описал свой метод приближенного графического нахождения корней многочленов произвольной степени (см. в Википедии «Метод Лиля»). Но только еще через 58 лет (в 1925 году) американский профессор Джордж Абрам Миллер, занимавшийся историей математики в качестве хобби, объяснил связь между окружностью, использованной Карлейлем и Лесли, и применением метода Лиля к решению квадратного уравнения.
Способ Карлейля
Итак, пусть мы хотим решить приведенное квадратное уравнение \(x^2-sx+p=0\). Тогда мы должны взять на координатной плоскости точки \(A\ (0;\ 1)\) и \(B\ (s;\ p)\), найти середину \(C\) отрезка \(AB\) и построить окружность с центром в \(C\) и радиусом \(CA\) (рис. 4). Точки пересечения этой окружности с осью абсцисс и будут корнями уравнения.

Рис. 4. Окружность Карлейля — определение
Доказательство практически полностью повторяет решение задачи Лесли, приведенное выше.
Но мы, кажется, собирались что-то строить циркулем и линейкой? А здесь координатная плоскость... Ничего страшного! Все, что нам на самом деле нужно от координат, вполне сводится к двум осям. Действительно, вместо точки \(B\ (s;\ p)\) можно сразу рассмотреть ее проекции на оси \(B_1\ (s;\ 0)\) и \(B_2\ (0;\ p)\). Ведь если мы знаем коэффициенты \(a\) и \(p\), то построить именно эти точки на осях — проще простого. А дальше центр окружности получится пересечением серединных перпендикуляров к \(OB_1\) и \(AB_2\) (постарайтесь разобраться, почему это так, по рисунку 5).

Рис. 5. Окружность Карлейля — построение
Как видно из рисунка 5, способ с окружностью Карлейля не только простой, но и удивительно легкий для запоминания. Кроме начала координат, требуются всего три точки — \(B_1\) (абсцисса которой равна коэффициенту \(s\)) откладывается на оси абсцисс, а \(A\ (0;\ 1)\) и \(B_2\) (ордината которой равна \(p\)) — на оси ординат. Два серединных перпендикуляра, одна окружность — вуаля, корни готовы!
Как это применять?
Возможно, самое известное применение окружностей Карлейля — построение правильных многоугольников. Многие слышали о том, что построение правильного пятиугольника циркулем и линейкой возможно. (На самом деле — не только возможно, но было дано и полностью обосновано еще Евклидом.) Но многие ли пытались понять, как именно решается эта задача?
Задача 2. Дана окружность с центром \(O\) и точка \(A\) на ней. Постройте правильный пятиугольник \(ABCDE\), вписанный в эту окружность.
Решение. Построение пятиугольника с помощью окружностей Карлейля отличается удивительной простотой. Начнем с координатных осей, проведя через центр круга прямую \(OX\), перпендикулярную \(OA\) (рис. 6). Радиус данной окружности будем считать равным 1. Теперь берем точку \(M\ (-1/2;\ 0)\) и строим окружность с центром \(M\), проходящую через \(X\). В пересечении с \(OA\) получаем точки \(H_1\) и \(H_2\). Если теперь в полученных точках построить единичные окружности, то они пересекут данную окружность как раз в точках \(B\), \(C\), \(D\), \(E\), являющихся вершинами правильного пятиугольника (на рисунке 6 он выделен красным, а единичные окружности — изображены синим пунктиром).

Рис. 6. Правильный пятиугольник
Почему это работает и при чем тут Карлейль? А вот при чем. Способ Карлейля утверждает, что построенная окружность с центром \(M\) находит корни квадратного уравнения для \(s;\ p)=(-1;\ -1)\), поскольку \(M\) — середина отрезка \(XY\), где координаты точки \(Y\) как раз и равны (\(-1;\ -1)\). Значит, \(H_1\) и \(H_2\) — корни квадратного уравнения \(x^2+x-1=0\). Это знаменитое уравнение золотого сечения. Для нас достаточно использовать его «тригонометрическую» ипостась.
Лемма. Корнями квадратного уравнения \(x^2+x=1\) являются величины \(2\cos72^{\circ}\) и \(2\cos144^{\circ}\).
Доказательство. Косинусы этих углов удовлетворяют тригонометрическому уравнению \(\cos3\alpha=\cos2\alpha\), при этом они отличны от корня \(\alpha=0\). Преобразование уравнения \(\cos3\alpha=\cos2\alpha\) в алгебраическое с помощью замены \(x=2\cos\alpha\) дает уравнение \((x-2)(x^2-x-1)=0\), что и требовалось доказать. (Корень \(x=2\) соответствует \(\alpha=0\).)
Итак, с помощью метода Карлейля и «золотой» леммы мы выяснили, что точки \(H_1\) и \(H_2\) имеют координаты \((2\cos144^{\circ};\ 0)\) и \((2\cos72^{\circ};\ 0)\) соответственно. А дальше мы в этих центрах построили единичные окружности, т. е. окружности того же радиуса, что и данная окружность с центром \(O\). Ясно, что они пересекут окружность \((O,\ A)\) на серединных перпендикулярах к отрезкам \(OH_1\) и \(OH_2\) соответственно. Осталось только понять, что серединные перпендикуляры — это прямые \(x=\cos72^{\circ}\) и \(x=\cos144^{\circ}\), а значит, точки \(B\), \(E\), \(C\) и \(D\) пересечения окружностей имеют координаты \((\cos72^{\circ};\ \sin72^{\circ})\), \((\cos72^{\circ};\ -\sin72^{\circ})\), \((\cos144^{\circ};\ \sin144^{\circ})\) и \((\cos144^{\circ};\ -\sin144^{\circ})\), т. е. углы \(AOB\) и \(AOE\) равны 72 градусам, а углы \(AOC\) и \(AOD\) — 144 градусам. А это и означает, что они являются вершинами правильного пятиугольника. Доказательство правильности построения на этом завершено.
О сложности построений и «геометрографии» Эмиля Лемуана
Француз Эмиль Мишель Гиацинт Лемуан по праву считается одним из отцов современной «геометрии треугольника». Вероятно, вы слышали о точке Лемуана в треугольнике или об окружностях Лемуана. Он же в 1892 году опубликовал работу «Геометрография, или искусство геометрических конструкций» («La Géométrographie ou l’art des constructions géométriques»), в которой впервые предложил сравнивать различные геометрические построения по количеству требуемых элементарных операций (а лучшим построением считать то, на которое тратится меньшее число операций). Оптимальным («геометрографическим») способом Лемуан называет самый экономный из известных алгоритмов построения.
Элементарных операций Лемуан насчитал пять:
\(S_1\) — приложить линейку к определенной точке;
\(S_2\) — провести прямую линию;
\(C_1\) — поставить ножку циркуля в определенную точку;
\(C_2\) — изменить радиус циркуля, поставив ножку с карандашом в определенную точку;
\(C_3\) — провести циркулем окружность.
При этом Лемуан считал циркуль устойчивым, т. е. после проведения окружности сохраняющим выставленный радиус. Таким образом, следующая окружность того же радиуса, по Лемуану, требует уже не трех операций: \(C_1+C_2+C_3\), а всего двух: \(C_1+C_3\).
Сосчитаем, например, количество операций в построении корней уравнения с помощью окружности Карлейля, показанном на рисунке 5. Оси координат и точки \(A\), \(B_1\) и \(B_2\) заданы. Построение серединного перпендикуляра к отрезку \(OB_1\) — это две окружности равных радиусов и одна прямая, т. е. \((2C_1+C_2+2C_3)+(2S_1+S_2)\). Следующий серединный перпендикуляр — это \((2C_1+2C_3)+(2S_1+S_2)\), потому что мы строим его, не меняя радиуса циркуля. Тем самым, мы построили центр, затратив 15 элементарных операций. И наконец, сама окружность Карлейля — это еще \(C_1+C_2+C_3\). Итого «сложность» построения \(5C_1+2C_2+5C_3+4S_1+2S_2\) равна 18.
Упражнение 1. Придумайте другой способ построения окружности Карлейля, имеющий сложность 17 или меньше.
Подсказка. Центр этой окружности — середина отрезка, одним из концов которого является \(B_1\). Постройте сначала второй конец этого отрезка.
Современная компьютерная игра-головоломка Euclidea (euclidea.xyz) также требует от решателей задач найти самое экономное построение, но, в отличие от Лемуана, не подсчитывает предварительные операции \(S_1\), \(C_1\) и \(C_2\), а считает только количество проведенных линий (т. е. \(S_2+C_3\) в терминологии Лемуана). С точки зрения Euclidea, построение окружности Карлейля имеет сложность 7.
Можно ли отыскать корни квадратного уравнения с меньшей сложностью?
Когда автор начинал писать эту статью, он предполагал, что этот вопрос будет повешен в качестве финальной улыбки Чеширского Кота и оставлен читателю для самостоятельного решения. Однако планы немножко поменялись, и сейчас я хочу показать более экономный способ, а читателям предложить обдумать, нельзя ли найти еще лучший.
Во-первых, откажемся от оси ординат. Зачем она нужна, если все корни мы ищем на оси абсцисс?
Пусть у нас есть всего одна ось, а на ней — четыре известные точки \(O\ (0)\), \(E\ (1)\), \(S\ (X+Y)\) и \(P\ (XY)\). Последние две точки соответствуют коэффициентам того уравнения, которое мы хотим решить. Рисунок 7 соответствует ситуации, когда \(0<XY<1<X+Y\), но это не очень критично — приведенное ниже построение работает и во многих других случаях, а если оно не будет работать из-за того, что какие-то окружности не пересекутся, то его не очень сложно адаптировать.
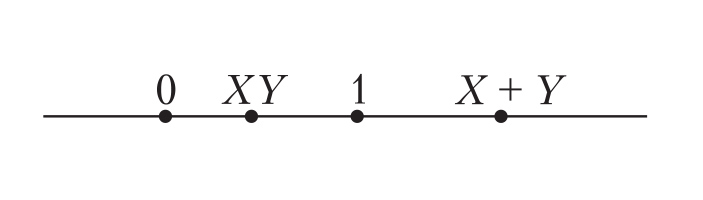
Рис. 7. Четыре точки на одной оси
Вначале проведем две окружности равных радиусов с центрами в \(P\ (XY)\) и \(E\ (1)\) (рис. 8) — как будто мы хотим строить середину отрезка между этими точками. Радиус окружностей возьмем таким, чтобы первая окружность прошла через точку \(S\ (X+Y)\). Отметим \(C\) — общую точку этих окружностей.

Рис. 8. Начало построения
Затем построим еще две окружности — окружность с центром \(O\ (0)\), проходящую через \(C\), и окружность такого же радиуса с центром \(S\). Их точку пересечения (любую из двух точек) назовем \(D\) (рис. 9).

Рис. 9. Вторые две окружности
И (немного неожиданный, как и полагается улыбке Кота) финальный шаг — окружность с центром \(D\), радиус которой точно такой же, как у двух первых (рис. 10). Нетрудно убедиться, что в пересечении этой окружности с осью абсцисс получатся нужные корни уравнения. Так получается потому, что разность квадратов радиусов построенных окружностей равна \(XY\), и по теореме Пифагора квадрат длины отрезка между точками пересечения пятой окружности с прямой равен \((X+Y)^2-4XY=(X-Y)^2\). А поскольку середина этого отрезка имеет координату \((X+Y)/2\), то правый конец отрезка совпадает с большим из чисел \(X\), \(Y\), а левый — с меньшим.

Рис. 10. Корни уравнения найдены
Сосчитаем сложность: \(2C_1+C_2+2C_3\) на первую пару окружностей, столько же на вторую и еще \(C_1+C_2+2C_3\) на последнюю окружность — всего \(5+5+3=13\), вместо прежних 17 или 18. Ура!
Дополнение.
Построение правильного 17-угольника
Задача 3. Пусть дана окружность с центром \(O\) и точка \(A\) на ней. Постройте правильный 17-угольник с вершиной \(A\), вписанный в эту окружность.
Эта задача, в отличие от трех неразрешимых задач древности, стала знаменитой после того, как была решена 19-летним Карлом Фридрихом Гауссом. Биографы Гаусса пишут, что только после ее решения Гаусс окончательно выбрал своей будущей профессией математику, а не литературу. Известна также легенда, что Гаусс завещал выбить на своем могильном камне изображение правильного 17-угольника. Кажется, даже если такое завещание было, то оно оказалось невыполненным, а вот на памятнике Гауссу в Брауншвейге след его юношеской работы есть (рис. 11 и 12).

Рис. 11. Памятник Гауссу в Брауншвейге
Полное описание гауссова метода решения этой задачи, пожалуй, далеко выходит за рамки одной статьи, но набросок метода дать нетрудно. Правда, это потребует от читателя хорошего знакомства с комплексными числами.
Решение. Основной идеей Гаусса было циклическое упорядочение комплексных корней 17-й степени из 1 — такое, чтобы каждый следующий корень был определенной степенью предыдущего. Он доказал, что полный цикл получится тогда, когда эта определенная степень равна 3.
Таким образом, он расположил корни в следующем порядке: \(\tau^1\), \(\tau^3\), \(\tau^9\), \(\tau^{10}\) (поскольку \(27=10(\mathrm{mod}\ 17)\)), \(\tau^{13}\), \(\tau^{5}\), \(\tau^{15}\), \(\tau^{11}\), \(\tau^{16}\), \(\tau^{14}\), \(\tau^{8}\), \(\tau^{7}\), \(\tau^{4}\), \(\tau^{12}\), \(\tau^{2}\), \(\tau^{6}\).
Далее Гаусс разбил этот цикл на два куска, которые он назвал периодами. В один период вошла половина корней — все корни на нечетных местах цикла, в другой — вторая половина:
\[\eta_{02}=\tau^1+\tau^9+\tau^{13}+\tau^{15}+\tau^{16}+\tau^{8}+\tau^{4}+\tau^{2},\\ \eta_{12}=\tau^3+\tau^{10}+\tau^{5}+\tau^{11}+\tau^{14}+\tau^{7}+\tau^{12}+\tau^{6}.\]Гаусс заметил, что сумма двух построенных им величин \(\eta_{02}+\eta_{12}\), равная сумме всех корней уравнения, равна \(-1\), а их произведение равно \(-4\). (Первое наблюдение Гаусса легко следует из теоремы Виета для уравнения \(x^{17}-1=0\), так как сумма всех корней вместе с корнем \(x=1\) равна 0. Второе же наблюдение несложно проверить непосредственным вычислением. Для этого достаточно просто перемножить выражения — каждое содержит по 8 слагаемых, в произведении их будет 64, и из соображений симметрии ясно, что каждая степень будет встречаться по 4 раза, поэтому произведение равно учетверенной сумме.) Иными словами, две эти величины — корни квадратного уравнения с известными коэффициентами.
Дальше — проще. Гаусс просто продолжает разбивать каждый период на два меньших:
\[\eta_{02}=\eta_{04}+\eta_{24},\]где \(\eta_{04}=\tau^1+\tau^{13}+\tau^{16}+\tau^{4}\), а \(\eta_{24}=\tau^9+\tau^{15}+\tau^{8}+\tau^{2}\),
\[\eta_{12}=\eta_{14}+\eta_{34},\]где \(\eta_{14}=\tau^3+\tau^{5}+\tau^{14}+\tau^{12}\), а \(\eta_{34}=\tau^{10}+\tau^{11}+\tau^{7}+\tau^{6}\).
Суммы значений \(\eta_{04}+\eta_{24}\) и \(\eta_{14}+\eta_{34}\) — уже известные нам величины \(\eta_{02}\) и \(\eta_{12}\), а их произведения равны \(-1\) (убедитесь в этом сами, раскрыв скобки в произведениях). Следовательно, мы снова знаем квадратные уравнения, корни которых нужно отыскать.
Следующим шагом точно так же вводятся периоды длины 2 — их всего восемь, от \(\eta_{08}\) до \(\eta_{78}\). Собственно, этот шаг уже является последним, потому что \(\eta_{08}=\tau^1+\tau^{16}=2\cos(\pi/17)\), так что, зная величину \(\eta_{08}\), мы легко построим вершины правильного 17-угольника, соседние с заданной вершиной \(A\) (аналогично построению вершин по точке \(H_2\) для правильного пятиугольника).

Рис. 12. Семнадцатиугольная звезда на памятнике
Упражнения
2. Вычислите произведение \(\eta_{08}\eta_{48}\).
3. Дуайн ДиТемпл описал пошаговое построение правильного 17-угольника с помощью окружностей Карлейля (commons.wikimedia.org). Разберитесь в этом построении.



















Томас Карлейль. Портрет работы Дэниэла Маклиса