Линза из Луны: ответы

Александр Бердников
«Квантик» №5, 2021

В «Квантике» № 3 за 2021 год была задача:

Представьте, что Луну заменили на линзу такого же диаметра, чтобы во времена солнечных затмений она фокусировала свет на поверхность Земли. Почему в этой ситуации такой «луч смерти» не представляет особой опасности?

Почему же такая большая линза не нанесёт вреда, если даже маленькой лупой можно поджечь бумагу или дерево? Конечно, зная подходящие формулы и величины, ответ можно вычислить. Но если удастся обойтись без этого, просто взглянув на ситуацию с другой стороны — будет, конечно, интереснее. Нам понадобится лишь пара отправных точек. Первая — что видимые размеры Луны и Солнца на небосводе близки — довольно банальна, это легко проверить самим (только не смотрите прямо на Солнце, когда оно яркое — это опасно для сетчатки глаза). А со второй сложнее: линза не меняет яркость поверхности, которую через неё видно. Хотя в этом легко убедиться самостоятельно, как предлагала подсказка в прошлом номере, тут есть много подводных камней, о них позже.

Рис. 1. Солнце обведено оранжевым, Луна-линза — голубым, её центр отмечен

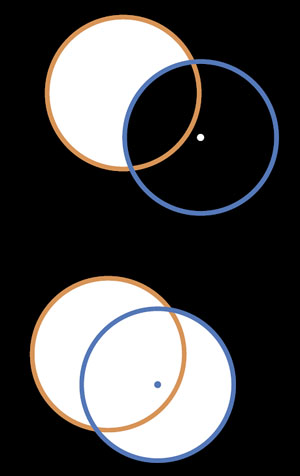
Представим теперь, как «затмение» Луной-линзой выглядит для его потенциальных жертв. Солнце мы будем считать частью фона-небосвода — до него на порядки дальше, чем до Луны. Итак, на небе будет видно Солнце, загороженное кругом Луны, а через линзу будет виден увеличенный маленький участок небосвода за центром линзы. Пока центр линзы не дополз до Солнца, будет обычное затмение, как вверху на рисунке 1 — мы через лупу смотрим в чёрный космос. Но когда в центре линзы окажется точка на Солнце, вся лупа засияет и Солнце будто примет форму этакой восьмёрки, как внизу на рисунке 1. Поскольку и яркость, и размер на небе у Луны-линзы станут такими же, как у Солнца, добавочного света от неё мы получим максимум как ещё от одного Солнца (которое, к тому же, будет частично загорожено). Приятного мало, но не смертельно: увеличение меньше, чем в два раза. А во время полного затмения вообще не будет большой разницы — тот же «солнечный» диск на небе, что и обычно.

Этот ответ вызывает ещё больше вопросов.

— Погодите, если освещённость со всей Луны собрать в одной точке, освещённость же возрастёт куда больше, чем вдвое!

Чтобы понять, почему это не так, попробуйте сфокусировать лупой свет лампы. Лампа не соберёт весь свет в одну точку: свет каждой точки лампы сойдётся в своей фокусной точке. Так и Луна сфокусирует на Земле большое изображение Солнца, а вовсе не точку.

— И что, свет так рассредоточится, что освещённость упадёт почти до обычной?

Рис. 2. Освещённость Земли при нормальном затмении и при затмении Луной-линзой

А какую площадь осветит Луна-линза? В пятно попадут все земляне, для кого линза «включилась». А для этого достаточно и частичного затмения (как на рисунке 1 внизу). Значит, для заметной части тени Луны на Земле линза уже «горит». Получается, солнечное пятно растянуто на площадь, сравнимую с лунной тенью, как на рисунке 2, так что не очень-то энергия и сфокусируется.

Задачка по геометрии — понять, что изображение Солнца будет размером как раз с Луну; вообще размеры линзы и изображения между собой не связаны, откуда совпадение в этом случае?

— А как же тогда выжигают обычные лупы? Как им удаётся собрать свет в точку?

Строго говоря, и лупы собирают свет не в точку. Они тоже дают изображение Солнца, просто маленькое — гораздо меньше, чем лупа. Вот освещённость и возрастает в сотни раз, пропорционально уменьшению площади. С точки зрения наблюдателя, в фокусе маленький круг Солнца сменится столь же сияющей лупой, которая займёт уже огромную часть неба: палить будет, как сотни солнц, которые потребовались бы для такого зрелища.

— Ладно, тут свет со всего Солнца собрали в пятнышко. Но мы через Луну-линзу смотрим на одну-единственную точку Солнца. Как получается, что она нам даёт столько же тепла, сколько обычно даёт всё Солнце?

Строго говоря, это можно обо всех лупах сказать. Да, нас теперь освещает «только одна точка», но куда большей частью своих лучей, чем обычно. Ведь теперь нам от неё достаются не только те лучи, что летели прямо на нас (это мизерная доля), а любые, попавшие в Луну (их куда больше). То, что в результате получается «ничья», — совпадение. Вспомните, что мы его вывели из равных видимых размеров Луны и Солнца.

— Да, а также из того, что лупа яркости не меняет. Но вот в телескоп звёзды видны ярче, чем глазом.

Вот и подводные камни появились. Про звёзды можно (с большими недомолвками!) сказать, что увеличивается их видимый размер, а не яркость поверхности. От них стало больше света, но его рассредоточение незаметно (звёзды что так, что эдак, точками видны) — вот и кажется, что они стали ярче.

— А в микроскопе, наоборот, при большом увеличении всё темнеет...

Микроскоп не может выдать больше света от рассматриваемой им пылинки, чем та в принципе даёт. Поэтому, чтобы слать нам всё большие её изображения с той же «настоящей» яркостью, приходится экономить и слать их в меньшее число точек. В итоге мы будто смотрим на увеличенную пылинку через уменьшенный зрачок (с оговорками): её изображение достаётся лишь части зрачка, а остальная его часть наблюдает вместо пылинки тёмные внутренности микроскопа, в среднем выходит темнее. Будь зрачок изначально сам маленький, он бы и так изначально получал меньше света и заметил бы потемнение только при больших увеличениях.

Фото 1. Солнце с несколькими видимыми пятнами. Два маленьких пятна в центре имеют такой же диаметр, как Земля

— А можно заявление про яркость всё-таки объяснить, почему она не меняется?

Строго сформулировать и вывести это — сложная математика (одно название пугает: «теорема Лиувилля о сохранении фазового объёма»). Скажем вот что: будь у нас лупа, меняющая яркость, можно было бы поставить её меж двух тел и перекачивать задаром энергию от одного к другому (тепловым излучением). Заманчиво, но природа такой щедростью не балует (это наблюдение составляет второй закон термодинамики).

— Осталось ещё придраться к «однородности» поверхности. Солнце-то разве однородно?

Не совсем. Во-первых, в центре Солнце поярче, чем с краю (фото 1): там мы видим глубже его раскалённые недра, а не смотрим вдоль менее горячего края. Но светлая середина и так большую часть Солнца занимает, и если всё оно будет такой яркости — невелика разница. Та же история и с гранулами, на которые разбивается поверхность Солнца (фото 2).

Фото 2. Гранулы на поверхности Солнца. Размер типичной гранулы ≈1500 км, существует она 8–20 минут. Фото: NSO/AURA/NSF

А вот при солнечной вспышке, когда вспыхнет малая его часть, из-за линзы вспышка не рассеется по всем зрителям равномерно, становясь едва заметной на общем фоне Солнца, как это было бы обычно. Вся энергия вспышки, пойманная Луной, достанется немногим «счастливчикам», попавшим в изображение этой вспышки на Земле. И здесь катастрофичность уже будет зависеть от того, как линза работает на других длинах волн, потому что на видимый свет приходится очень малая часть энергии вспышки...

Вот так на один простой вопрос можно отвечать, уходя всё дальше, но когда-то нужно и остановиться.

Художник Алексей Вайнер