Три креста, или Чемпионское разрезание
Николай Авилов
«Квантик» №1, 2021
Давайте докажем с помощью разрезаний геометрическое равенство:
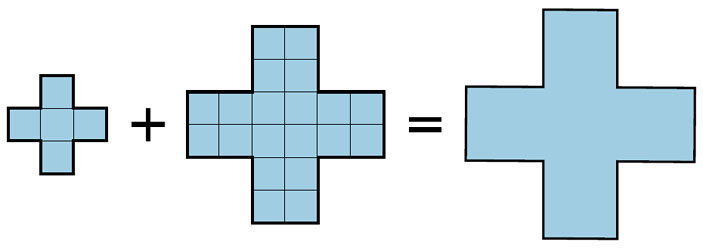

Задачи на разрезание многоугольников — одни из самых увлекательных, и что интересно: если надо разрезать многоугольник на несколько частей и сложить из них другой, это всегда возможно, лишь бы многоугольники имели равные площади!1
В нашей задаче суммарная площадь двух меньших крестов равна 5 + 20 = 25, значит, сторона квадратов, из которых составлен большой крест, равна \( \sqrt{5} \). Отрезок длиной \( \sqrt{5} \) нетрудно получить, если вспомнить, что гипотенуза прямоугольного треугольника с катетами 1 и 2 равна \( \sqrt{5} \). Сразу непонятно, как резать кресты, поэтому предлагаю решить задачу-помощницу для квадратов со сторонами 1, 2 и \( \sqrt{5} \):
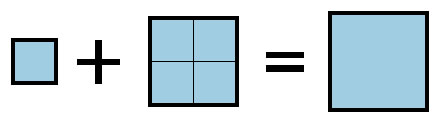
Тут решение почти очевидное: если разрезать квадрат со стороной 2 на четыре треугольника с катетами 1 и 2, из них легко сложить квадрат:
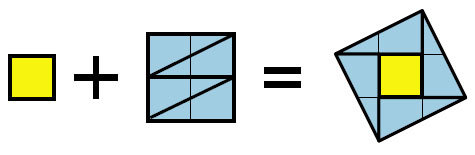
Теперь понятно, какой должна быть сторона третьего креста. Так как каждый крест состоит из пяти квадратов, то, разрезая каждый из них по приведённой схеме, получим решение нашей задачи:
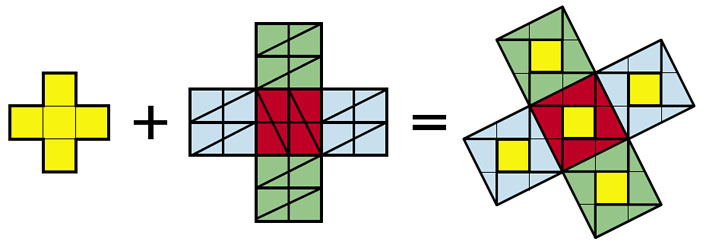
В этом решении большой квадрат разрезан аж на 25 частей. Но в подобных задачах особо ценятся разрезания на небольшое число частей. Найти минимальное разрезание — почти всегда трудная задача, требующая немало фантазии.
Поищем более экономное разрезание. Попробуем не разрезать маленький крест. Для этого поместим его в центре, как показано на рисунке. Оказывается, каждую из четырёх оставшихся частей можно замостить четырьмя прямоугольными треугольниками (такими же, как в задаче-помощнице). Значит, найдено разбиение на 21 часть, что меньше 25:
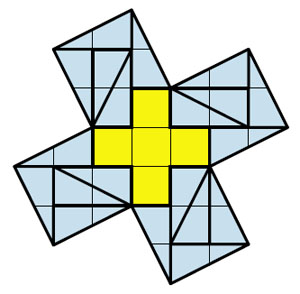
Но «бросается в глаза» большое количество равных прямоугольных треугольников. Попытаемся объединить их в фигуры, которыми можно замостить средний по величине квадрат. Посмотрите на результат — разноцветный калейдоскоп, где «спрятано» более экономное разрезание, всего на 9 частей:
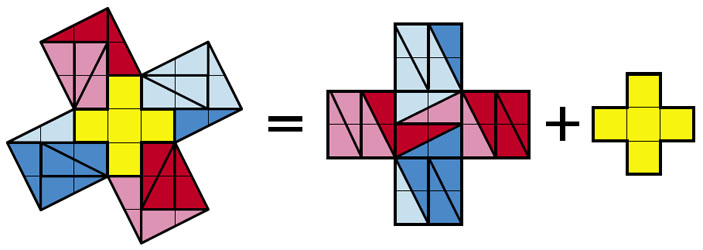
С таким решением эта задача долгое время лежала в моём архиве, пока не попала к Василию Илюхину — чемпиону России по решению головоломок. Он поступил нестандартно, наложив средний крест на большой, да ещё с выходом за границу большого креста. На первый взгляд, это кажется бесполезным. Но это же чемпионский ход!
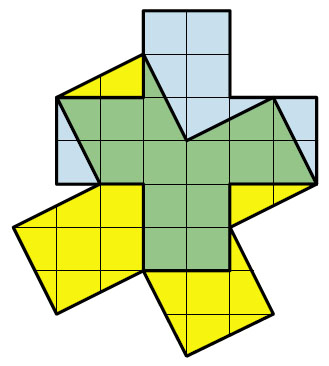
Оказывается, все голубые участки среднего креста можно уложить на жёлтые участки большого креста, предварительно отрезав от наибольшего куска прямоугольный треугольник с катетами 1 и 2. А малый крест разрезается на две части. В итоге получается разрезание на 7 частей.
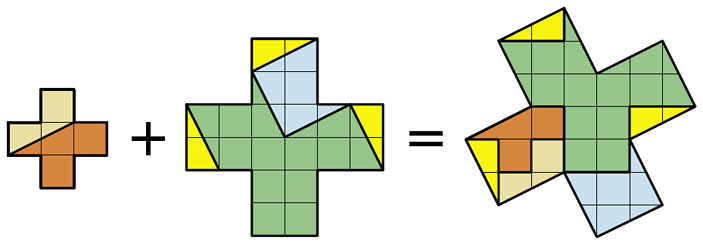
Можно ли разрезать на число частей меньшее, чем 7? Этот вопрос пока остаётся открытым! Обязательно напишите нам, если вы найдёте решение.
И напоследок — задача Л. П. Мочалова. С помощью разрезания докажите равенство:

Художник Алексей Вайнер
1 Это утверждение известно как теорема Бойяи — Гервина. Доказательство можно прочитать в брошюре В. Г. Болтянского «Равновеликие и равносоставленные фигуры».


















