Пирамида из квадрата
Задача
Разрежьте квадрат на пять частей, которые можно переложить так, чтобы получилась развертка правильной четырехугольной пирамиды. Можно ли обойтись меньшим числом частей?
Подсказка 1
а) Разрежьте квадрат по четырем отрезкам, соединяющим середины его соседних сторон.
Подсказка 2
б) Можно обойтись меньшим числом частей.
Решение
а) Если квадрат со стороной 2а разрезать по четырем отрезкам, соединяющим середины его смежных сторон, а затем переложить отрезанные треугольники к центральному квадрату так, чтобы они прилегали вершинами прямых углов и катетами, то получим четырехугольную звезду (рис. 1). Нетрудно показать, что она равносторонняя и что все ее стороны равны по \(a\sqrt2\), а значит, это развертка правильной четырехугольной пирамиды. Основанием пирамиды служит центральный белый квадрат, а прилегающие к нему равнобедренные треугольники — боковыми гранями.

б) Можно. Невыпуклый семиугольник, похожий на ракету (рис. 2, слева), является разверткой правильной четырехугольной пирамиды, в основании которой лежит квадрат со стороной а, а все ее боковые грани — равносторонние треугольники со стороной а. Покажем, что эту развертку можно сложить из равновеликого ей квадрата, разрезав на четыре части. Площадь всей развертки равна \(a^2(1+\sqrt3)\), тогда сторона AD равновеликого ей квадрата ABCD должна быть равна \(a\sqrt{1+\sqrt3}\). Построим квадрат ABCD так, чтобы середина M стороны AD совпадала с серединой стороны квадрата, являющегося основанием пирамиды (рис. 2, справа). При таком построении пятиугольники 1 и 1' симметричны относительно точки M, поэтому они равны. По этой же причине равны и пятиугольники 2 и 2'. Но тогда равны и треугольники 3 и 3', значит, развертка «ракета» и квадрат ABCD равносоставлены, поэтому, разрезав квадрат ABCD на четыре части (1', 2', 3' и 4), можно из них составить развертку «ракета» и сложить пирамиду.

Рис. 2.
Послесловие
Задачи на разрезание пользуются популярностью у любителей математики, а решение таких задач почти всегда похожи на маленькие открытия. Покажем это на примере рассматриваемой задачи и проследим ее историю.
Все задачи, придуманные мною, первыми решают мои ученики. И иногда им удается найти новые решения, отличные от авторского. Так было и с этой задачей. Простое и естественное ее решение нашел Иван Кушнарев, участник летней математической школы. Оно показано на рис. 3. Все отрезки на этом рисунке, отмеченные одним штрихом, имеют длину \(\frac{a}4\), а отрезки, отмеченные двумя штрихами, — длину \(\frac{a}2\). Квадрат разрезается на два пятиугольника и три треугольника из которых можно сложить развертку правильной четырехугольной пирамиды, изображенную справа.

Рис. 3.
Позже задача появилась в журнале «Математика в школе». Вот одно из присланных после этого решений. На рис. 4 слева показано разрезание квадрата на четыре дельтоида и малый квадрат. Здесь тоже все отрезки, отмеченные одним штрихом, равны четверти стороны разрезаемого квадрата, а отмеченные двумя штрихами — ее половине. Справа показана «вертушка», сложенная их этих четырехугольников, которая является разверткой пирамиды. Штриховыми отрезками на ней показаны ребра правильной пирамиды, основанием которой является желтый квадрат. Кстати, этот способ разрезания приводит к пирамиде из предыдущего решения.

Рис. 4.
В августе 2017 года задача победила в конкурсе группы «Математические задачи и головоломки» на Facebook. Участники этого конкурса нашли очень много решений.
Вот, например, решение Константина Кнопа. При каждой стороне исходного квадрата нужно вырезать одинаковые треугольники таким образом, что, переложив их по-другому, можно получить равносторонний восьмиугольник, являющийся разверткой правильной пирамиды (рис. 5).

Рис. 5.
Кроме этого, взяв за основу решение известной задачи квадрирования «вертушки», Константин построил динамический чертеж в GeoGebra. Это дало бесконечное семейство решений с разными пирамидами. Все пирамиды правильные, потому что их боковые грани — равные равнобедренные треугольники, но с разными углами при вершине, величина которых изменяется от 45° до 90°. На рис. 6 показано решение, в котором из квадрата получается правильная пирамида с углом при вершине 60°. Посмотреть динамический чертеж можно здесь.

Рис. 6.
Решение пункта б) придумал А. Домашенко. Найдено оно с помощью двух паркетов. Первый паркет замощен симметричными развертками правильной пирамиды, похожую на ракету, второй замощен квадратами, равновеликими этой развертке пирамиды (рис. 7).

Рис. 7.
При наложении этих паркетов получается мозаика (рис. 8), в которой можно разглядеть решение пункта б), приведенное выше.

Рис. 8.
Более 20 лет проводятся ежегодные матчи между командами России и Украины по решению головоломок. Организаторы этих матчей в 2017 году включили обсуждаемую здесь задачу в число конкурсных, и она принесла победные баллы в копилку команды России, участник которой В. Илюхин нашел разрезание квадрата всего лишь на три части (рис. 9).
По отрезку, соединяющему середины смежных сторон квадрата, отрезается треугольник, затем вырезается равнобедренная трапеция, у которой боковые стороны и меньшее основание равны. Таким образом исходный квадрат разрезан на три части: треугольник, трапеция и невыпуклый семиугольник. Из этих фигур складывается одиннадцатиугольник, который является разверткой правильной четырехугольной пирамиды. На рис. 9 справа штриховыми отрезками показаны линии сгибов, которые являются ребрами пирамиды. Также было показано, что даже при разрезании на три части есть бесконечное семейство решений.

Рис. 9.
Подводя итоги, можно сказать, что квадрат можно разрезать любое, большее двух, число частей, из которых можно сложить развертку правильной четырехугольной пирамиды. Также есть «разрезание» и на одну часть: можно загнуть углы квадрата к центру и получить правильную четырехугольную «пирамиду» нулевой высоты. Если это считать решением, то остается только случай n = 2. Существует ли подходящее разрезание на две части?
Можно заметить, что каждая новая публикация этой задачи приносила новые решения и продвижения. Хочется, чтобы это случилось и на «Элементах».
-
Аффигеть!
Но раз каждое решение похоже на открытие, делаю вывод, что общего алгоритма лля поиска решений на разрезание нету?
А кажется, открытие такого алгоритма - это задачка ничуть не менее симпатичная, чем теорема Ферма!)-
Пирамиду нулевой высоты можно получить разрезанием квадрата на любое количество частей, а не только на одну, если после разрезания квадрата все части оставить на месте 😀
-
Именно об этом речь идет в заключительной части послесловия, что квадрат можно разрезать на любое число частей и сложить пирамиду, но для числа 2 вопрос открытый!
-
-
Теперь я понял, что правильную четырехугольную «пирамиду» нулевой высоты нужно исключить, иначе задача теряет смысл!
-
Ну, зачем так радикально! Уважаемый Олег же, полагаю, пошутил!)
Нуль-высотную пирамиду можно оставить, только
"противоолеговое" условие ввести: площадь поверхности получаемой пирамиды не должна быть равна удвоенной площади исходного квадрата!))
Хотел сначала сказать, что площадь найденной пирамиды должна быть равна площади исходного квадрата, но решил ограничить только исключением удвоенной площади, в надежде, что Олег Чечулин счас что-то еще неожиданное, не запрещенное условиями соорудит!))
-
-
-
-
-
Последние задачи


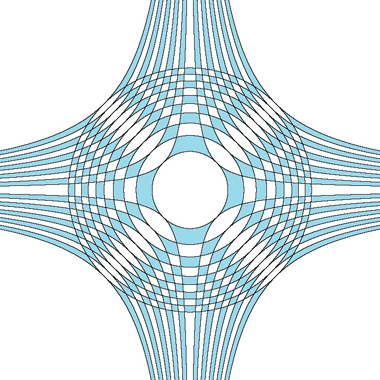












Рис. 1.