Таблетка от забывчивости
Александр Перепечко
«Квантик» №9, 2020

Чтобы решить задачу и помочь Саше, мы отправимся в путешествие по разноцветным гирляндам, графам де Брёйна и цепям Маркова.
Граф де Брёйна
В статье «Разноцветные гирлянды» («Квантик» № 12 за 2017 год) мы строили гирлянду из красных и синих флажков, в которой встречаются все наборы из фиксированного числа флажков, например из 3. Эти наборы удобно изображать стрелками. Сначала нарисуем всевозможные двухфлажковые наборы и обведём каждый набор кружком. А потом для каждого трёхфлажкового набора проведём стрелку, ведущую из кружка с первыми двумя флажками набора в кружок с последними двумя флажками набора: например, стрелка ▼▼▼ ведёт из ▼▼ в ▼▼ (рис. 1). Это и будет стрелка, соответствующая трёхфлажковому набору. Будем красить стрелки в тот же цвет, что и последний флажок соответствующего набора. Тогда из каждого набора выходит и в каждый набор входит по одной синей и одной красной стрелке. Такие картинки из кружков и стрелок называются ориентированными графами. А если картинка построена по наборам флажков, она называется графом де Брёйна.
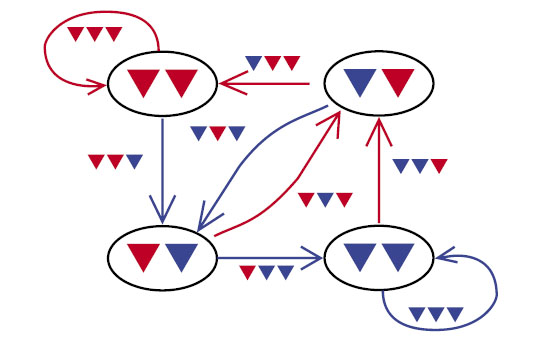
Рис. 1

Маршрут вдоль стрелок, в котором каждая стрелка встречается ровно один раз, как раз даёт минимальную гирлянду, содержащую все наборы, как в статье «Разноцветные гирлянды».
Как же построить такой маршрут? Особенно если цветов больше, или наборы состоят из большего числа флажков? Придёт на помощь правило «только не красный»: начнём с набора из красных флажков, а далее каждый раз, если можем, выходим по стрелке не красного цвета. Оказывается, таким способом мы обойдём все стрелки по одному разу и тем самым построим гирлянду. Это непростая теорема из комбинаторики. Попробуйте сами понять на примерах разных гирлянд, почему так происходит, и смотрите доказательство теоремы в конце статьи.
Цепь Маркова
Как всё это связано с задачей про таблетки? Будем отмечать каждый пропущенный приём таблетки красным флажком, а не пропущенный — синим. Тогда последние два флажка полностью описывают текущее состояние, и всего разных состояний — 4 (рис. 2). Стрелки обозначают приписывание нового флажка.

Рис. 2

Из крайних состояний нет выхода, а из средних Саша может переместиться левее или правее с вероятностью \(\frac{1}{2}\). Это всё равно что подкидывать монетку с красной и синей сторонами: если выпадает красное, то Саша смещается влево, а если синее — вправо.
Саша начинает в позиции ▼▼ (синий флажок — таблетка, принятая утром у врача, до этого таблетки не принимались). Может ли быть такое, что Саша никогда не попадёт в крайние положения? Это возможно только если Саша будет попеременно выкидывать красное и синее. При каждом броске вероятность этого сокращается вдвое и тем самым стремится к нулю. Значит, вероятность того, что Саша всегда будет то принимать таблетку, то забывать, равна нулю. Это событие невероятное, но теоретически возможное.
В каких случаях Саша закончит в левом положении, а в каких — в правом? Можно выписать все возможные исходы: скажем, в правое положение приводят последовательности бросков ▼, ▼▼▼, ▼▼▼▼▼ и т.д. Их бесконечное количество, и придётся суммировать бесконечный ряд вероятностей: \(\frac{1}{2}\), \(\frac{1}{8}\), \(\frac{1}{32}\) и т. д. С этим можно справиться, например как в статье Г. Мерзона «\(\frac{1}{3}\), или Две невозможные задачи с решениями» («Квантик» № 6 за 2019 год).
А можно посмотреть на вероятности иначе: предпишем каждому текущему состоянию вероятность попасть из него в крайнее правое состояние, то есть вероятность успеха в лечении. Эта вероятность никак не зависит от того, каким путём мы попали в текущее состояние. Тогда в крайнем правом состоянии будет вероятность 1, а в крайнем левом — 0. Докажем, что вероятность в промежуточном состоянии равна полусумме вероятностей в соседних. Пусть для состояния слева вероятность успеха равна а, а справа — b. Равновероятно мы идём влево или вправо, то есть достигаем успеха с вероятностью \(\frac{1}{2}·a\) (идём влево) плюс \(\frac{1}{2}·b\) (идём вправо). Это как раз полусумма а и b.

Нетрудно проверить, что тогда разность вероятностей для каждой пары соседних состояний будет одна и та же (получается арифметическая прогрессия), и поскольку разностей 3, все они равны \(\frac{1}{3}\). Так что вероятности попасть в крайнее правое положение равны 0, \(\frac{1}{3}\), \(\frac{2}{3}\), 1 соответственно. Итак, Саша с вероятностью \(\frac{2}{3}\) станет постоянно принимать таблетки, а с вероятностью \(\frac{1}{3}\) — перестанет их принимать.
Решим этим методом известную задачу о пьянице.
Задача о пьянице. Пьяница стоит на дороге между кабаком и своим домом и каждую секунду делает шаг в 1 м по дороге в случайном направлении с равной вероятностью. Если попадает домой или в кабак — остаётся там. Спрашивается, с какой вероятностью он придёт домой, если до дома — 3 м, а до кабака — 7 м?
В этой задаче 11 состояний (рис. 3), вероятности крайних — 0 и 1, вероятность сдвига вправо (домой) — \(\frac{1}{2}\). Опять же, вероятности промежуточных состояний образуют арифметическую прогрессию, и ответ: \(\frac{7}{10}\).
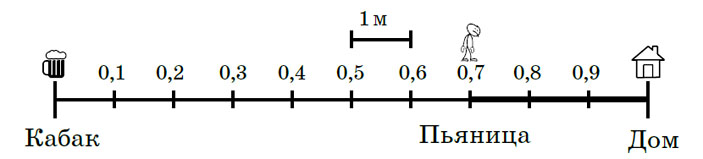
Рис. 3
А вот похожая задача про Сашу:
Задача «утро — день — вечер». С какой вероятностью Саша успешно излечится, если он вспоминает о приёме таблетки с вероятностью k/3, где k — количество принятых таблеток в последние 3 приёма?
Попробуйте решить её самостоятельно.
Задачи, где есть набор состояний и вероятности перехода между ними, описываются так называемыми цепями Маркова. Но это уже совсем другая история.
Обход графа де Брёйна
Вернёмся к графам де Брёйна. Как же нам обойти все стрелки?
Граф де Брёйна обладает двумя свойствами: во-первых, в нём из любой вершины можно дойти по стрелкам до любой другой (то есть он связен), а во-вторых, в каждую вершину (так называются наши кружки) входит столько же стрелок, сколько и выходит. Такие графы обладают удивительным свойством: можно, начав в любой вершине, пройти по каждой стрелке один раз и вернуться в исходную вершину. Такой обход называется эйлеровым циклом, а такой граф называется эйлеровым (см. также статью «Почтовое занятие», «Квантик» № 6 за 2020 год).
Начнём из «красной» вершины (соответствующей набору красных флажков) и будем бродить по стрелкам, не проходя одну стрелку дважды и соблюдая правило «только не красный»: мы выходим из вершины по «красной» стрелке (соответствующей приписыванию красного флажка), только если других исходящих стрелок не осталось.
Каждый раз, входя в вершину, мы уменьшаем количество непройденных входящих стрелок, а выходя — исходящих. То есть во всех вершинах сохраняется равенство входящих и исходящих стрелок, кроме исходной — в ней на одну входящую больше, и текущей — в ней больше на одну исходящую. Значит, закончим мы обязательно в исходной вершине, то есть получим цикл.
Почему же этот цикл эйлеров? Заметим два свойства:
- Если по этому циклу мы вышли из какой-то вершины по «красной» стрелке, то мы уже прошли по всем стрелкам, входящим и исходящим из этой вершины. Действительно, если мы вышли по «красной» стрелке, то мы уже перебрали все остальные, а также вошли столько же раз, сколько и вышли.
- По «красным» стрелкам можно дойти от любой вершины до «красной» вершины.
Предположим, что по каким-то стрелкам мы не прошли. Из всех вершин, в которые входят непройденные стрелки, выберем такую, из которой путь по «красным» стрелкам к «красной» вершине самый короткий. Тогда исходящая «красная» стрелка должна лежать в цикле (иначе найдётся путь короче), но это противоречит первому из замеченных свойств. Значит, цикл действительно эйлеров!
По эйлерову циклу графа де Брёйна уже легко построить гирлянду: берём флажки, соответствующие одной из вершин, а потом из этой вершины обходим эйлеров цикл, с каждой стрелкой добавляя новый флажок. Более того, первые флажки, соответствующие исходной вершине, совпадут с последними, и, склеив их, мы можем «сшить» гирлянду в кольцо. Тогда каждый флажок будет в точности соответствовать одной стрелке. Это кольцо можно разорвать в любом месте, продублировав флажки в месте разрыва, и получить новую гирлянду.
Вообще говоря, любой связный граф, в котором в каждую вершину входит столько же стрелок, сколько и выходит, обладает эйлеровым циклом. Как мы уже увидели, если мы начнём бродить из произвольной вершины по стрелкам без повторений, мы получим какой-то цикл. Но если убрать все стрелки этого цикла, то в новом графе по-прежнему будет равенство входящих и исходящих стрелок в каждой вершине. Значит, мы можем снова и снова так ходить и удалять циклы, пока не исчерпаем все стрелки, и разобьём исходный граф в объединение циклов. Здесь нам даже не нужна связность графа.
А вот чтобы склеить все циклы в один, связность понадобится. Благодаря ей, мы можем найти два цикла, проходящие через одну вершину, и склеить их, пройдя из этой вершины сначала по одному циклу, а потом по второму. Рано или поздно останется один цикл — эйлеров.
Художник Мария Усеинова
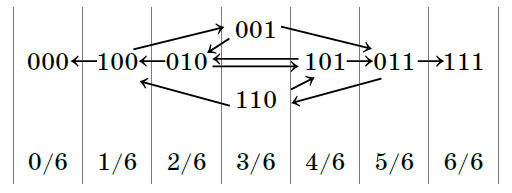
Ответ
Удивительно, но граф состояний в задаче «утро — день — вечер» (см. рисунок) можно уложить на дорожку длиной в 6 шагов, при этом состояния 001 и 110 (когда Саша принял таблетку только в последний раз, и когда Саша принял таблетку все разы, кроме последнего) окажутся вместе. Из каждого состояния можно пойти в одну сторону на один шаг с вероятностью \(\frac{1}{3}\) или на два шага в противоположную сторону с вероятностью \(\frac{2}{3}\). Поэтому вероятности успеха вновь образуют арифметическую прогрессию. Значит, при исходном положении 001 вероятность успеха — \(\frac{1}{2}\).