Гравитационный бильярд и механическая модель лазерного резонатора

Андрей Андреев, Алексей Панов
«Квантик» №6, 2018

Из-за разности давлений плёнка принимает сферическую форму

Для создания гравитационного бильярда нам понадобится стеклянная банка, воздушный шарик и ещё стальной шарик диаметром в несколько миллиметров. На стеклянную банку натянем кусок резиновой плёнки, вырезанной из воздушного шарика. Перед тем как герметично закрепить плёнку, нажмём на неё и выпустим из банки немного воздуха, чтобы под действием атмосферного давления плёнка прогнулась внутрь. Если банка круглая, то из-за разности давлений плёнка примет сферическую форму — будет представлять собой небольшой кусочек сферы.

Если на нашу плёнку с малой высоты точно по центру отпустить небольшой металлический шарик, он будет многократно подскакивать вверх и снова падать в центр, и эти подскоки будут продолжаться достаточно долго (видео).

Шарик отпускается точно по центру плёнки

Если же начальная высота превышает некоторое критическое значение, то, как бы точно мы ни прицеливались по центру плёнки, всё равно после нескольких отскоков шарик будет выброшен за её пределы (видео).

Оказывается, что критическая начальная высота, разделяющая эти два типа траекторий, равна половине радиуса сферы, частью которой является наша плёнка. Это можно проверить экспериментально, а можно доказать и чисто математически.

А теперь отключим гравитацию — представим, что мы находимся в условиях невесомости. Возьмём две такие банки, расположим их друг против друга и запустим между ними стальной шарик.

В невесомости

Возникает аналогичный вопрос: при каких условиях шарик будет устойчиво двигаться, попеременно отражаясь от одной плёнки к другой, а при каких условиях его обязательно выбросит из пространства между банками?

На самом деле это важный вопрос, и он хорошо изучен. Дело в том, что у нашей механической системы имеется известный оптический аналог. Это лазерный резонатор — система из двух сферических зеркал, расположенных друг против друга. Он характеризуется тремя числами: радиусами зеркал R₁, R₂ и расстоянием между вершинами зеркал L.

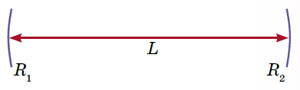
Схема лазерного резонатора

В зависимости от соотношения этих трёх параметров световой луч, движущийся вблизи оси резонатора, либо всегда остаётся внутри резонатора, либо после нескольких отражений вылетает оттуда. В первом случае резонатор называют устойчивым, и его можно использовать для генерации лазерного излучения, во втором случае резонатор называют неустойчивым.

Отыскание критерия устойчивости лазерного резонатора — увлекательная задача, и её можно решить с помощью школьной математики. На сайте «Квантика» (PDF, 13 Мб — просматривать лучше в режиме 2 страницы на экран) вы найдёте подробное обсуждение этой задачи, одинаково применимое и к самому лазерному резонатору, и к его «двухбаночной» механической модели.

Фото авторов
Художник Артём Костюкевич