Поющий ключ

Александр Бердников
«Квантик» №9, 2016

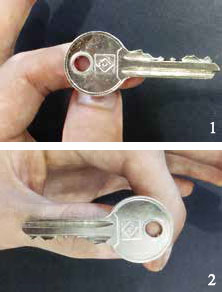
Добудьте цельнометаллический ключ примерно такой формы, как на фото 1. Его можно заставить звенеть разными способами. Можно подвесить ключ на тонкой ниточке и легонько ударить чем-нибудь твёрдым. Скорее всего, ключ издаст чистую высокую ноту. А теперь положим его на палец (как на фото 1) и подкинем сильным щелчком, будто бросая жребий. Звук окажется примерно той же высоты, но заметно «грязнее», будто кто-то нажал несколько соседних клавиш на фортепиано. Почему так происходит?

Может быть, ключ на ниточке ударили аккуратно, и поэтому у него звук чистый, а подброшенный ключ сильно щёлкнули — вот он и дребезжит? Нет, объяснение какое-то уж очень расплывчатое, да и не выдерживает простейшей проверки. А именно, попробуем подкидывать ключ разными щелчками: если щёлкать строго по центру, как на фото 2, а не по боку, звук окажется заметно чище.

Может быть, всё зависит от того, в какое место мы ударяем ключ? Грязным был звук при ударах по боку, а чистым — при ударе по центру, не в этом ли разгадка? Но почему тогда высота звука в обоих случаях одна и та же? На простое совпадение это не спишешь: можно подбрасывать ключи разной формы, но высота звона у каждого из них оказывается постоянной, как его ни щёлкай. А можно изловчиться и так ударить ключ на ниточке, чтобы он быстро закрутился вокруг своей оси, как при броске жребия, но висел довольно ровно (не делая скачков). Тогда вообще можно услышать, как изначально грязный звон становится чище, пока ключ останавливается.

Значит, звук крутящегося ключа — это просто искажённый звук ключа неподвижного, и важно именно вращение ключа, а не особенности удара. Можно заметить, что чем быстрее вращается ключ, тем сильнее искажение. Одно такое явление широко известно — это эффект Доплера: чем быстрее что-то приближается к вам, тем выше кажутся его звуки (а если удаляется — то ниже). Вспомните, например, как меняется звук проносящейся мимо машины или мотоцикла. У вращающегося ключа тоже одна половина к нам приближается, а другая отдаляется. Выходит, мы должны услышать вместо одной ноты две: одну — чуть выше исходной (от приближающейся части), другую — чуть ниже (от отдаляющейся).

Рис. 1

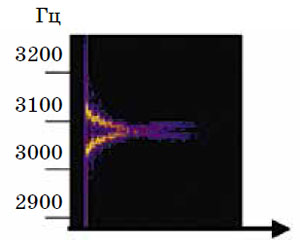
Посмотрим на спектрограмму (рис. 1). Она показывает частоты, издаваемые висящим на ниточке ключом, который ударили по боку (высота ноты отложена по вертикали, время — по горизонтали; частота измеряется в герцах (Гц); чем больше частота звука, тем выше нота). На рисунке и вправду видны две ярких линии, то есть две ноты. Ключ, перекручивая нитку, быстро останавливается, и на спектрограмме видно, как при этом частоты сближаются, сливаясь в одну. Когда ключ остановится, нитка начнёт его раскручивать в обратную сторону, и на спектрограмме сошедшиеся было ноты опять расходятся.

Хотя объяснение искажения звука с помощью эффекта Доплера и подкрепилось спектрограммой, у него есть множество нестыковок. Чтобы обнаружить первую из них, подкиньте ключ так, чтобы его ось вращения была направлена примерно на вас. Эффект Доплера должен пропасть — ведь расстояние до любой части ключа почти не меняется. Однако на практике звук остаётся столь же грязным (расстояние между близкими частотами не уменьшается), хоть и становится тише.

Рис. 2

Вторая нестыковка хитрее. Начнём с того, что на самом деле ключ даже без кручения издаёт много нот, правда, далёких друг от друга. Обычно мы замечаем только самый нижний звук, а остальные воспринимаем как его окраску, тембр. Но они, тем не менее, вполне реальны и при вращении ключа расщепляется каждый из них. И будь дело в эффекте Доплера, расщепление высоких нот было бы больше, чем у нижних. Это следует из такого свойства эффекта Доплера: при данной скорости он меняет все частоты в одно и то же число раз (скажем, на 3% для скорости 10 м/с), и тогда расщепление у вдвое более высокой ноты будет вдвое шире, и т. п. Однако посмотрим на спектрограмму на рисунке 2. На ней видны сразу три ноты звона ключа: основная (нижняя яркая) и две повыше (тусклые). Каждую из них из-за вращения ключа фактически разделило на две. И, хотя частота исходных нот различается в разы, расстояние между их «потомками» почти одно и то же. А это совсем не похоже на эффект Доплера.

И третья нестыковка: а действительно ли эффект Доплера должен делать из каждой ноты две? Мы сказали, что у вращающегося ключа половина движется к нам, половина от нас, но это очень неточно. Ведь это неправда, что все движущиеся к нам части приближаются с одной и той же скоростью. У каждой части ключа своя скорость: та, что ближе к оси, — помедленнее; та, что дальше, — побыстрее. Звук от каждой части в результате сместится на свою величину, так что в итоге нота не разделится на две, а скорее «размажется».

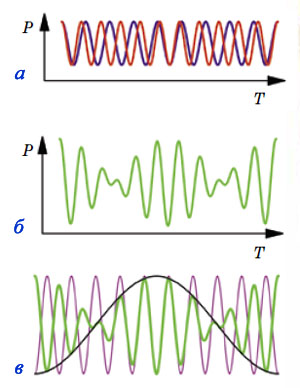
Рис. 3

Но почему же тогда каждая нота ключа делится надвое? Зайдём-ка с другого конца. А как вообще устроен грязный звук близких нот? Одна чистая нота — это колебание давления воздуха с фиксированной частотой (его график — красный на рисунке 3а, P — давление, T — время). Если мы добавим другой звук, с близкой частотой (синий на рисунке 3а), то их вклады в давление воздуха сложатся. Пусть в какой-то момент они колеблются практически синхронно, так что получаются вдвое большие колебания (более громкий звук). Это не может продолжаться долго: скорость у колебаний немножко разная, так что они скоро разойдутся и начнут гасить друг друга, вместо того чтобы усиливать (звук пропадёт). Спустя ещё некоторое время колебания опять синхронизируются, и так далее. В результате получится будто бы одна нота, которая то затихает, то снова появляется¹ (график на рисунке 3б).

Последнее замечание можно сформулировать и изобразить по-другому (рис. 3в): наш зелёный график (сумма двух близких нот) похож на звук некой промежуточной частоты (фиолетовый), у которого меняется со временем громкость, или «размах» колебаний («размах» изображён в виде чёрного графика). Центральная часть зелёного графика действительно так и получается из фиолетового, а вот справа и слева от центра зелёный график оказался ещё и «перевёрнут» по сравнению с фиолетовым.

В этом нашем наблюдении и кроется разгадка, главная идея решения. Попробуем разобраться и понять физический смысл нарисованной картинки.

Нота постоянной частоты (фиолетовый график) у нас есть: это звон ключа. Когда ключ не вращается, мы слышим эту чистую ноту. Теперь нужно понять, почему её громкость начинает колебаться, если ключ закрутить. Это тоже несложно: скажем, когда ключ повёрнут к нам «лицом» (то есть мы смотрим перпендикулярно его плоскости), ключ звучит на нас всей своей поверхностью, и звон его громок. Потом он развернётся к нам ребром, мы «слушаем» маленькую его поверхность, и звон становится тихим. Затем ключ ещё повернётся, и звон опять вернётся на полную громкость, и так далее. Эти изменения легко заметить у медленно крутящегося ключа.

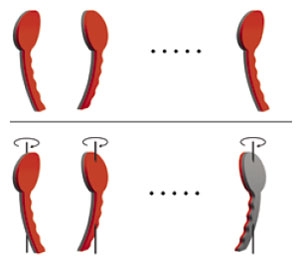
Рис. 4

Такое объяснение вполне согласуется с центральной частью рисунка 3в. А откуда берётся «переворачивание» звука по краям? Чтобы разобраться, покрасим мысленно одну сторону ключа в красный цвет. Рассмотрим для примера колебания такого вида: то концы ключа отогнутся в покрашенную сторону, а середина — в непокрашенную, то наоборот (верхний ряд на рисунке 4). Такие колебания дадут одну ровную ноту. Теперь вспомним, что у нас ключ ещё и вращается (нижний ряд на рис. 4). И, после того как ключ сделает пол-оборота, изгибания, одинаковые с точки зрения самого ключа (крайние в обоих рядах на рисунке 4) для нас окажутся «противоположными». Значит, и звук после полуоборота не просто вернёт себе громкость, но его колебания «сменят знак» (вращающийся ключ звенит то «в ногу» с неподвижным, то «в противоход» с ним). Это мы и видим на рисунке 3в: фиолетовый и зелёный графики то почти одинаковы, то почти противоположны.

В итоге эти изменения амплитуды чистой ноты дают, как мы убедились, тот же результат, что и сложение двух близких нот (это просто другое описание того же самого звука). Вот мы и слышим какофонию. А если ключ закручен медленно, мы воспримем его звон «как положено», чистой нотой с меняющейся громкостью.

Итак, одна нота ключа, громкость которой меняется из-за его вращения, слышится как две². Такое объяснение изменения звона свободно от всех предыдущих недостатков и полностью согласуется с опытами. Например, величина расщепления ноты получается зависящей лишь от периода обращения ключа — ни высота ноты, ни ориентация оси ключа на это расщепление не влияют.

Рис. 5

Проверим себя. На верхнем графике рисунка 5 записан звук ключа на ниточке. Отдельные колебания тут сливаются, видна только громкость — толщина (по вертикали) синей полоски. На втором — колебания, вычисленные по описанной нами модели (но без учёта эффекта Доплера). Для построения использовалась усреднённая скорость вращения ключа, измеренная камерой. Видно, что на обоих графиках громкость колеблется совсем одинаково, замедляясь по мере того, как перекрученная ключом ниточка замедляет его вращение. Для сравнения, на нижнем графике учтён, наоборот, только эффект Доплера, а изменения амплитуды из-за ориентации ключа проигнорированы.

Рис. 6

Другая проверка — спектрограммы звона ключа (первая слева на рисунке 6) и трёх наших моделей: с учётом лишь колебания амплитуды (вторая), лишь эффекта Доплера (третья) и обеих (четвёртая).

Видно, что найденная нами модель отлично описывает явление. При этом важным оказалось лишь изменение ориентации ключа и вызванные им колебания громкости, а эффект Доплера никакого заметного вклада не внёс. Малость эффекта Доплера можно было бы понять заранее, зная, что ширина ключа заметно меньше длины волны. Как — задача (сложная) для самостоятельного обдумывания.

Художник Ольга Демидова

¹ Такие колебания громкости, возникающие от сложения близких нот, называются биениями. Извлечём на гитаре одну и ту же ноту на двух струнах сразу. Если звуки окажутся немножко разными, мы легко услышим биения. Поэтому они помогают при настройке.

² Выходит, мы нашли эффект, обратный биениям, при которых, наоборот, близкие ноты слышны как одна с колеблющейся громкостью.