«Математический беспредел». Глава из книги

Сравнивая бесконечности

Когда у ребенка впервые получается взобраться на первую ступеньку лестницы, процесс поглощает его. Теперь ему хочется вскарабкаться на следующую ступеньку, а потом на следующую. Он очень удивлен, что может настолько высоко забраться, всего лишь повторяя одно и то же новое действие, которому только что научился. Если ребенку вдруг удалось преодолеть особенно высокую ступеньку, то он очень этому радуется.

Только что мы с вами научились взбираться на особенно высокую ступеньку: мы узнали, как добраться от одной бесконечности до еще большей бесконечности. И в точности как маленький ребенок, восхищенный своей новой способностью преодолевать ступеньки, мы хотим карабкаться дальше, взобраться на следующую ступеньку, а потом еще выше. Наши ступеньки не настоящие ступеньки, это даже не «ступеньки-числа». Это ступеньки лестницы в бесконечность.

Теперь давайте сравним вот такие факты:

• Действительные числа более бесконечны, чем натуральные.
• Если бесконечность натуральных чисел обозначается как ω, то существует 2^ω действительных чисел.

А сейчас мы будем повторять одно и то же действие, чтобы доказать, что так мы сможем получить все более бесконечные бесконечности вечной иерархии бесконечностей. Конечно, сначала мы должны определиться с тем, что, в конце концов, означает «более бесконечные бесконечности».

Главный вопрос: как сравнивать размеры бесконечностей? Мы уже решили, что действительные числа несчетные, то есть их невозможно в точности соотнести с натуральными числами, потому что некоторые действительные числа обязательно будут пропущены. На интуитивном уровне ясно, что действительных чисел должно быть «больше», чем натуральных, но что конкретно это означает, если и те и те бесконечны? Одни бесконечности больше, чем другие бесконечности. Как это возможно с учетом того, что бесконечность уже бесконечно велика? Разве бесконечность не есть уже самое большое, что существует в мире? Как что-то может быть больше нее?

Такие вопросы, как и разговоры о душе, о вечной жизни или о том, поправилась я или нет, в конечном итоге сводятся к необходимости дать точное определение всем понятиям. Что имеется в виду под словом «толстая»? В нашем случае вопрос будет звучать так: что мы имеем в виду, говоря «большой»? Мы можем махнуть рукой и сказать: это не имеет никакого значения, потому что бесконечность и так бесконечно большая. Но математики не склонны махать руками, пока не обнаружат фактическое логическое противоречие. Если существует явление, которое интуитивно кажется разумным, то математики стремятся обнаружить среду, в которой оно будет разумным и с логической точки зрения. Так проявляется наше упрямство. Если во время горного восхождения тропинка выводит меня к обрыву, я начинаю нервничать и поворачиваю назад. Но если я вижу математический обрыв, то есть пропасть между интуитивным восприятием и логикой, то я без страха устремляюсь к нему, чтобы изучить его вблизи.

Как правило, для этого мне необходимы точные определения понятий. Вам кажется, что мы ходим по кругу? Если я хочу доказать, что я не толстая, то могу взять мой индекс массы тела в качестве оценочного параметра, и тогда, согласно большинству «официальных» определений этого понятия, получится, что я в норме. Но если я хочу, наоборот, доказать, что я толстая, то я могу взять в качестве оценочного параметра соотношение талии и бедер, в этом случае согласно большинству определений этого понятия, я толстая (что предполагает также риск диабета).

Кажется, что использование точных определений в своих целях уводит нас от стандартного математического мышления. Начиная изучать какой-либо объект, скажем числа, первым делом мы проверяем, что верно для чисел, а что нет. Например, что получится, если сложить 3 и 4? А что получится, если сложить 4 и 3? Ага, ответ один и тот же. Так мы обнаружили нечто, что является верным при сложении чисел.

Однако дальше в математике все идет по-другому, даже если раньше вы этого не замечали. Самый простой пример — решение уравнений. Например, дано такое уравнение:

3х + 4 = 10.

Вы говорите: я хочу, чтобы это равенство стало верным. Какое значение переменной x сделает его верным? Многое в высшей математике действительно начиналось с мечты. А потом ты берешься за работу и создаешь мир, в котором эта мечта становится реальностью. (Я думаю, что это похоже на мечты в обычной жизни.)

В случае с бесконечностью мы можем сказать: «Я хочу, чтобы одни бесконечности были больше, чем другие». Какое точное определение слова «больше» может исполнить мое желание? Ранее мы на примере доказали, что действительных чисел очевидно «больше», чем натуральных, хотя и те и другие бесконечны. Теперь мы можем использовать этот факт как точное определение для понятия «более большая бесконечность». Посмотрим, что произойдет. А произойдет кое-что интересное: мы узнаем, как построить иерархию все больших и больших бесконечностей.

Сравнивая множества объектов

В предыдущей главе мы выяснили, что действительные числа несчетные, доказав, что все попытки объединить их в пары с натуральными числами обречены на провал: как минимум одно действительное число останется в одиночестве. Мы можем использовать этот метод для сравнения любых двух множеств. Вот так он работает для очень маленьких множеств:

Мы уже приводили этот пример раньше. Число 16 справа осталось без пары. Что бы мы ни делали, справа обязательно будет стоять число без пары, и не обязательно именно 16.

Если все попытки объединить объекты множеств А и В в пары приводят к тому, что как минимум один объект справа остается без пары, то можно сказать, что множество справа «больше».

В некотором смысле это похоже на простейший способ, которым маленький ребенок часто пользуется, чтобы узнать, сколько у него предметов, когда он еще не научился считать. Например, чтобы узнать, хватит ли ему печенья поделиться с друзьями, он отдает по одной штучке тому, кто умеет считать, и тот, скорее всего, будет считать вслух каждое полученное печенье. Чтобы узнать, что в «Танцах со звездами» знаменитостей столько же, сколько профессионалов, мы просто должны убедиться, что они объединены в пары. Это значит, что их одинаковое количество. При этом не нужно считать всех участников, потому что нам необязательно знать, сколько их всего. Но, даже если мы посчитаем их, это будет не что иное, как соотнесение группы людей с официальной числовой сумкой. Скажем, у нас есть десять участников. Если вы будете их считать, то фактически вы будете просто создавать пары с множеством чисел:

{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

Если вы объедините участников в пары с этим множеством чисел и выясните, что числа 9 и 10 не были использованы, то станет понятно, что у вас меньше десяти участников. А если вы объедините участников в пары и выясните, что числа 9 и 10 были использованы два раза, то станет понятно, что у вас больше десяти участников.

При столь малом количестве объектов множества такой детальный анализ не требуется, это будет перебор. Однако это очень типичная для математики проблема. Вы начинаете изучать ее с простых ситуаций, но они слишком просты и для них совсем не нужны никакие глубокие математические познания, поэтому рассуждения кажутся бессмысленными. А если вы сразу приметесь за изучение действительно сложных ситуаций, то это будет слишком трудным началом.

В любом случае такой способ объединения объектов в пары — это еще одна из уловок маленьких детей, не умеющих считать. Например, ребенок хочет посадить в каждый вагон своего лего-поезда по одному лего-человечку. Если человечки закончились, но остались пустые вагоны, то ребенок понимает, что человечков не хватает. Это очевидно, даже если он не знает, ни того, сколько всего у него человечков, ни того, сколько человечков требуется для заполнения каждого вагона. Когда мы имеем дело с бесконечными множествами, мы должны точно так же поступать с понятиями «больше» и «меньше», потому что мы тоже не знаем, сколько всего объектов во множестве, если это множество бесконечно большое.

Давайте представим, что у нас бесконечное количество лего-человечков и мы должны поместить их в бесконечный лего-поезд. Мы хотим узнать, что «более» бесконечно: человечки или вагоны. Возможно, вы думаете, что если в конце поезда у нас останутся пустые вагоны, значит, нам не хватает человечков. Первая проблема здесь заключается в том, что мы не можем точно сказать, что значит «конец поезда». Если мы начнем размещать наших бесконечных человечков в вагонах (неважно, бесконечны вагоны или нет), это будет длиться «вечно», и мы так никогда и не доберемся до конца поезда. Но давайте не будем обращать внимание на этот факт, ведь мы рассуждаем теоретически и вовсе не обязаны делать что-либо подобное в реальности.

Вот способ, с помощью которого мы можем поместить человечков в вагоны и получить пустые вагоны в конце поезда. Мы перепрыгиваем первый вагон, предположив, например, что первый человечек похож на меня и тоже не любит ездить в первом вагоне, опасаясь аварий. Мы помещаем первого человечка во второй вагон, второго человечка — в третий вагон и так далее. Таким образом мы заполняем все оставшиеся вагоны. В итоге у нас получается один пустой вагон, но это вовсе не значит, что у нас не хватает человечков. Мы можем сдвинуть всех на один вагон назад, и тогда все вагоны будут заняты.

Мы можем даже оставить в начале поезда бесконечное количество пустых вагонов. Например, мы хотим поместить человечков только в четные вагоны, тогда мы занимаем вагоны 2, 4, 6, ... и так далее, точно так же, как в одном из сценариев эвакуации отеля Гильберта. В этом случае все нечетные вагоны останутся пустыми. Кажется, что у нас не хватает человечков, но мы точно знаем, что это не так.

Это одна из тех невероятных и удивительных вещей, которые происходят, когда имеешь дело с бесконечностью. А значит, теперь мы снова должны либо махнуть рукой, либо более внимательно отнестись к определению понятий. Мы можем перегруппировывать наши бесконечные множества различными невероятными способами, так что в некоторых случаях будут использоваться все вагоны, а в некоторых — нет. Это похоже на заселение еще одного гостя в заполненный отель Гильберта. Подобное невозможно, если у вас есть, скажем, всего десять человечков и десять вагонов. Если вам нужно поместить по одному человечку в каждый вагон, то вы тоже можете разместить их множеством разных способов, но как только у вас закончатся человечки, у вас одновременно закончатся и вагоны. А если у вас есть какое-нибудь другое конечное множество человечков и вагонов и у вас закончились человечки, но остались пустые вагоны, то вы точно будете знать, что вагонов было больше, чем человечков.

В случае с бесконечным количеством человечков и бесконечным количеством вагонов вы можете использовать всех человечков, и у вас при этом могут остаться пустые вагоны, но вы не будете точно знать, можно ли перегруппировать человечков так, чтобы были использованы все вагоны. Если вы хотите доказать, что у вас больше вагонов, чем человечков, то вы должны убедиться в том, что невозможно перегруппировать человечков таким образом, чтобы абсолютно все вагоны были использованы, а человечки остались. Кажется, что это очень труднодоказуемо, но мы уже однажды делали нечто подобное при помощи диагонального аргумента Кантора. Тогда мы доказали, что не существует идеального отображения действительных и натуральных чисел, потому что если бы оно было возможно, то как минимум одно действительное число всегда оставалось бы без пары.

В математике в этом случае мы не используем слово «больше», так как оно звучит недостаточно точно. Мы сейчас говорим об очень специфической величине «крупности», которой лучше дать более точное определение. Правильное математическое слово для нее — «мощность множества». Мощность множества объектов — это величина, показывающая, сколько в нем объектов. Если множество содержит в себе конечное количество объектов, то его мощность — это просто количество этих объектов. Если множество содержит бесконечное количество объектов, то все будет немного сложнее. Мы все еще похожи на маленького ребенка, который не умеет считать: мы можем определить, что два множества имеют одинаковую мощность, мы также можем определить, что одно множество больше другого, но мы не можем точно сказать, чему фактически равна мощность множеств. Тем не менее мы уже научились строить бесконечные множества со все большей и большей мощностью.

Самая маленькая бесконечность

Наименьшее из возможных множеств — пустое. Поэтому самая маленькая возможная мощность множества равна 0. Далее следуют все возможные конечные варианты множеств: множество из одного объекта, множество из двух объектов, множество из n-го количества объектов, где n — любое конечное число.

Получается, что натуральные числа — это самое маленькое из возможных бесконечных множеств. Однако мы помним, что под «самым маленьким» в данном случае имеется в виду точная величина, которая определяется методом создания пары для каждого объекта множества. Что мы подразумеваем, говоря, что бесконечное множество «меньше» множества натуральных чисел? Мы хотим сказать, что это другое бесконечное множество, удовлетворяющее следующему условию: если мы попытаемся объединить его объекты в пары со всеми натуральными числами, то как минимум одно натуральное число обязательно останется в одиночестве.

Давайте рассмотрим это снова на примере эвакуации гостей отеля Гильберта. У вас бесконечное количество гостей, но после их эвакуации в другой отель обязательно останутся свободные комнаты. Хотя потом мы всегда можем «переэвакуировать» всех так, что ни один номер не будет пропущен. Для этого мы должны попросить гостей в новом отеле переместиться так, чтобы все комнаты были заняты. Звучит несколько неопределенно, но мы можем дать гостям точную инструкцию: «Посчитайте, сколько человек проживает в комнатах с номером меньше, чем ваш. Прибавьте к их количеству единицу и переезжайте в комнату с таким номером».

• Тот, у кого будет самый маленький номер, прибавляет ноль человек, потому что ни у кого нет номера меньше, чем у него. Значит, он переезжает в комнату с номером 0 + 1 = 1.
• Тот, у кого следующий после этого самый маленький номер, прибавляет одного человека и переезжает в комнату с номером 1 + 1 = 2.

Эти рассуждения еще не совсем похожи на доказательство, однако их уже можно назвать концепцией доказательства того, что можно создать пары из всех объектов любого бесконечного подмножества натуральных чисел и всех натуральных чисел. Это значит, что любое подмножество натуральных чисел либо является конечным, либо имеет ту же самую мощность множества, что и множество всех натуральных чисел. Между ними нет бесконечности. Так мы выяснили, что самая маленькая из возможных бесконечностей — это бесконечность размером с натуральные числа.

Мы научились создавать разные размеры бесконечности, теперь нужно подумать о более удачном обозначении для бесконечности. В ситуациях, когда нужно быть предельно внимательными к размерам бесконечности, мы используем запись ℵ₀. Такой символ называют «алеф». Это первая буква древнееврейского алфавита, а индекс 0 означает, что это самая маленькая из возможных бесконечностей, самое начало иерархии бесконечностей. Такое обозначение читается как «алеф-ноль».

Следующая бесконечность

Мы уже повстречали много бесконечностей, которые оказались одинакового размера с множеством натуральных чисел. Некоторые из них кажутся меньше, но на самом деле таковыми не являются. Например, множество четных или множество нечетных чисел. Или даже еще более яркий пример: множество чисел, кратных 100. Или числа, кратные миллиону. Это лишь крошечная (одна миллионная) доля натуральных чисел, но это все равно бесконечность с мощностью, равной мощности множества всех натуральных чисел. Теперь утверждение «бесконечность, деленная на миллион, остается бесконечностью» приобретает смысл. Мы также можем рассмотреть отдельно числа более 100. И они тоже будут бесконечностью размером с множество натуральных чисел. И утверждение «бесконечность минус 100 равно бесконечность» тоже становится осмысленным.

Мы уже увидели бесконечности, которые кажутся больше, но на самом деле таковыми не являются. Например, два множества натуральных чисел: красное и синее. Или три множества, или счетное бесконечное количество множеств натуральных чисел. Или множество всех целых чисел, или даже множество всех рациональных чисел. Мы уже убедились в том, что объекты всех этих бесконечных множеств могут быть объединены в пары с натуральными числами. Это доказывает, что все они тоже являются ℵ₀.

Однако мы повстречали только одно множество, которое на самом деле больше множества натуральных чисел: это множество действительных чисел. Вопрос теперь заключается в том, можно ли назвать его следующей по величине бесконечностью? Этот крайне сложный вопрос можно решить с помощью континуум-гипотезы¹. «Континуум» в данном случае означает действительные числа, потому что они способны заполнить собой всю числовую ось «непрерывно», в отличие от целых чисел или рациональных чисел, которые оставляют пропуски. Континуум-гипотеза называется гипотезой, потому что она не доказана. Эта гипотеза, высказанная Георгом Кантором в 1878 году, предполагает, что мощность множества действительных чисел является следующей по величине бесконечностью после бесконечности натуральных чисел. Ее также можно сформулировать по-другому: не существует множества, размер которого находится в промежутке между множеством натуральных чисел и множеством действительных чисел. Это означает, что если некий объект вырвется на свободу и станет больше множества натуральных чисел, то ему все равно будет суждено быть лишь равным множеству действительных чисел. Правда это или нет, доказать невозможно. В одних мирах это правда, в других — ложь, все зависит от того, какой мир вы выберете.

Следующая по величине бесконечность после ℵ₀ должна называться ℵ₁. Континуум-гипотезу еще можно сформулировать следующим образом: континуум действительных чисел равен ℵ₁. В этом вопросе мы можем пойти дальше, так как из предыдущей главы нам уже известно, чему равна мощность множества действительных чисел в отношении к мощности множества натуральных чисел. А значит, если мощность натуральных чисел равна ℵ₀, то количество действительных чисел будет 2^ℵ₀ (при использовании двоичных дробей).

Возможно, вы заметили, что если бы мы использовали десятичные дроби, то ответ был бы 10^ℵ₀. Двоичная система более разумна с точки зрения математики по нескольким причинам. Во-первых, потому что 10 — это странное произвольное число, применяемое при счете действительных чисел, исключительно потому, что у нас десять пальцев и мы предпочитаем десятичную систему исчисления на базе 10. А вот число 2 — вовсе не произвольное: это самая маленькая из возможных баз.

Другая причина еще логичнее: 2^ℵ₀ выглядит меньше, чем 10^ℵ₀. А ведь мы как раз ищем то, что меньше, то есть пытаемся выяснить, можно ли множество 2^ℵ₀ назвать следующей, меньшей по величине бесконечностью после 10^ℵ₀. Будет логично выразить ответ так, чтобы он выглядел меньше. Формально нет никакой разницы, ведь бесконечность размера 2^ℵ₀ равна бесконечности размера 10^ℵ₀. Фактически они обе равны 1 000 000 000 000^ℵ₀, но если я скажу вам, что это и есть следующая по величине бесконечность после ℵ₀, то вы можете спросить, так ли важна в данном случае первая часть числа, то есть «1 000 000 000 000». Если мы остановимся на 2^ℵ₀, то все становится понятнее: для того, чтобы создать следующую по величине бесконечность, нужно возвести некое число в степень предыдущей бесконечности, даже если ее размер был всего лишь 2.

Возможно, сейчас вы вспомнили, что раньше мы игнорировали знаки до запятой. Это было довольно бесцеремонно с моей стороны, но на самом деле тут нет большой разницы. Но давайте исправляться. Знаки перед запятой — это целая часть числа. Нам известно, что существует ℵ₀ целых чисел. Значит, нужно умножить количество наших действительных чисел на ℵ₀ — так мы допускаем все возможные целые числа. Однако умножение гиганта 2^ℵ₀ на счетную бесконечность не сделает бесконечность больше. Скажу по секрету, я всегда знала об этом, именно поэтому меня не особенно волновали знаки до запятой.

Геометрический способ выразить это заключается в том, что, игнорируя целую часть числа, мы считаем только действительные числа от 0 до 1. А теперь давайте посмотрим на отрезок числовой оси с этими действительными числами. Сколько раз мы должны будем скрепить части этого отрезка, чтобы он стал непрерывным? По одному разу на каждое натуральное число, так что у нас будет ℵ₀ копий этого отрезка. Более того, мы можем ограничиться любым отрезком оси действительных чисел (даже самым крошечным, размер тут не имеет значения), и на нем всегда будет одно и то же общее количество чисел. Один из способов убедиться в этом — биективное отображение, то есть создание идеальных пар между числами крошечного отрезка и числами от 0 до 1. Например, давайте рассмотрим только действительные числа от 0 до 1/100. Представьте, что мы хотим объединить их в пары с действительными числами от 0 до 1. Для этого нам нужно просто умножить их на 100 и составить пары с ответами. Это все, что требуется. Похоже на перенос маленького кусочка числовой оси на большую ось.

Теперь, когда мы знаем, чему равна мощность множества всех действительных чисел, мы можем записать континуум-гипотезу в виде уравнения:

ℵ₁ = 2^ℵ₀

Итак, мы научились взбираться на первую ступеньку лестницы в бесконечность. Если у вас математический склад ума, то сейчас вы (в точности как маленький ребенок) стремитесь повторить то, чему вы только что научились, и возвести 2 в степень этой новой бесконечности. В более обобщенной версии континуум-гипотезы говорится, что на любом этапе это кратчайший путь добраться до новой, большей по величине бесконечности. Так мы можем получить иерархию бесконечностей, или алефов,

ℵ₀, ℵ₁, ℵ₂, ℵ₃, ...,

где в каждом случае ℵ_n+1 = 2^ℵ₀. Это еще более сложный вариант континуум-гипотезы, поэтому мы не можем доказать, что кратчайший путь к созданию серии увеличивающихся бесконечностей действительно именно такой, но мы можем попытаться увидеть, как бесконечности будут увеличиваться.

Эти бесконечности действительно больше?

Если ℵ₀ — это «размер натуральных чисел», то как можно возвести 2 в его степень? Обычно мы определяем 2ⁿ как «2, умноженное на само себя n раз», но с бесконечностью это не сработает, потому что вы не можете «умножить число 2 на само себя бесконечное количество раз».

Ключевой момент — перестать воспринимать 2ⁿ как нечто, что мы можем делать только с числами, и вспомнить, что мы рассматриваем мощность как размер конкретного множества или, если хотите, официальной числовой сумки. Так, n фактически — это размер множества n объектов. Давайте не будем смотреть на 2ⁿ как на размер некоего множества по отношению к множеству n объектов. Идея в том, чтобы создать концепцию, которая будет разумной для конечных чисел, а потом применить ее к бесконечным множествам, потому что мы знаем, что ℵ₀ — это не что иное, как размер множества натуральных чисел.

Мы вскоре убедимся в том, что это похоже на выбор обуви для отпуска. Принимая это важное решение, вы можете либо долго глядеть на всю вашу обувь, выбирая из всего количества те пары, которые вы хотите взять с собой; либо поочередно рассматривать каждую пару и задавать себе вопрос: да или нет. Итак, сколько может быть возможных комбинаций? Если у вас всего две пары, скажем, кроссовки и сандалии, то выбор такой:

• Вообще ничего не брать. Ходить босиком.
• Взять только сандалии.
• Взять только кроссовки.
• Взять и кроссовки, и сандалии.

Всего четыре возможных варианта. Другой способ посчитать все варианты — метод «да или нет». Чтобы им воспользоваться, нужно нарисовать дерево принятия решения:

(И да, если вы действительно возьметесь рисовать дерево принятия решения, чтобы выбрать из двух пар обуви, то все будут смеяться над вами, потому что это абсурд. Хотя весьма в духе математиков. Я известна тем, что иногда рисую схемы оптимизации времени, проведенного на кухне за приготовлением угощения для большой вечеринки, но я всегда стараюсь поскорее выбросить эти схемы, чтобы их никто не увидел.)

Возможно, вы вспомнили это дерево. Точно такое же мы уже рисовали для выбора вариантов меню и для двоичных дробей. А если у нас будет три пары обуви, то дерево будет выглядеть так:

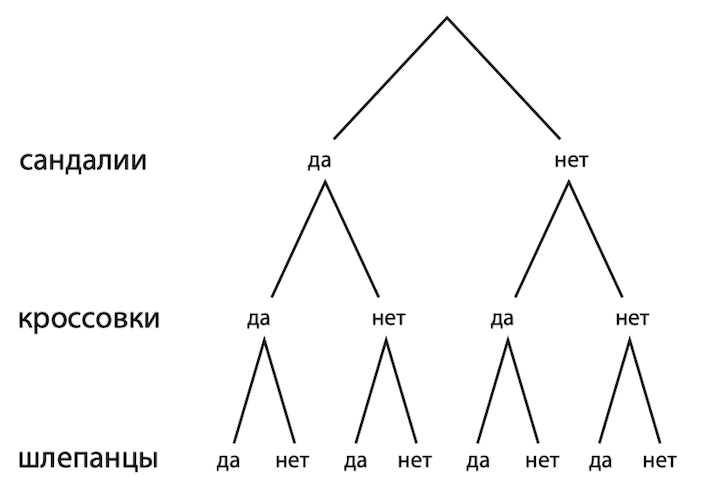
Теперь общее количество возможных вариантов будет 2 × 2 × 2 = 2³ = 8.

Если у нас n-е количество пар обуви, то у нас будет 2ⁿ возможных вариантов, точно так же, как итоговое количество двоичных дробей с n-м количеством десятичных знаков.

Теперь нам осталось только перенести этот алгоритм на случаи, когда n будет равно бесконечности. Это называется генерализацией, и это очень важная часть математического мышления. Вы изучаете хорошо знакомые вещи, а потом пробуете перенести концепцию на что-то менее знакомое, не нарушая при этом исходные условия этой концепции. Мы уже вскользь упоминали «бесконечные деревья», но тогда это были лишь робкие попытки заглянуть в неизвестность. Сейчас мы будем действовать гораздо точнее.

Выбирая обувь для отпуска, мы получили 2ⁿ. Это подмножество нашего общего множества обуви. Вывод: если в нашем распоряжении есть n пар обуви, то у нас будет 2ⁿ возможных подмножества обуви, которую мы можем взять с собой в отпуск.

Эта концепция работает даже при n, равном бесконечности, то есть если n будет любой интересующей нас версией бесконечности. Начнем с натуральных чисел. Мы определили мощность множества натуральных чисел как ℵ₀. Теперь рассмотрим множество всех возможных подмножеств натуральных чисел. Определим мощность этого множества как 2^ℵ₀. Мы не стали считать мощность этого множества, а просто воспользовались идеей возвести 2 в бесконечную степень, сделав это так, чтобы получилось конечное множество значений степени для числа 2.

Нет никакой надежды на то, что однажды у нас получится записать все возможные подмножества для множества всех натуральных чисел; с другой стороны, мы никогда не сможем записать все натуральные числа. Фактически ситуация сложилась еще хуже. Подмножества натуральных чисел несчетные, а значит, бессмысленно пытаться составить их список. Это невозможно даже теоретически, как минимум одно число будет пропущено.

Получается, что мы можем использовать нечто вроде диагонального аргумента Кантора для того, чтобы доказать, что набор подмножеств всегда больше самого множества. Если речь идет о конечных множествах чисел, то все вполне очевидно. Независимо от того, сколько всего у вас пар обуви, возможных обувных комбинаций для отпуска у вас будет еще больше. С бесконечными множествами то же самое, и это можно доказать, хотя дело тут обстоит немного сложнее. По тому, как мы считаем 2n, уже ясно, что 2n всегда будет больше, чем n. Это значит, что вот эта наша предполагаемая иерархия бесконечностей

продолжаясь, действительно будет увеличиваться. Итак, независимо от того, насколько велика наша бесконечность, мы всегда можем получить еще большую бесконечность, использовав свойство набора всех ее подмножеств.

А значит, когда в детском споре речь заходит о бесконечности, то для того, чтобы сделать свою бесконечность больше, нужно сказать: «Я прав два в бесконечной степени раз!». Продолжение спора будет выглядеть примерно так:

«А я прав два в бесконечной степени два в бесконечной степени раз!»

«А я прав два в бесконечной степени два в бесконечной степени два в бесконечной степени раз!»

...

¹ Континуум-гипотеза, или первая проблема Гильберта, — любое бесконечное подмножество континуума является либо счетным, либо континуальным. Континуум-гипотеза стала первой из двадцати трех математических проблем, о которых Давид Гильберт доложил на II Международном конгрессе математиков в Париже в 1900 году. — Примеч. ред.

² Система аксиом Цермело — Френкеля (ZF) является стандартной системой аксиом для теории множеств. Названа в честь Эрнста Цермело и Адольфа Френкеля. Современная теория множеств строится на системе аксиом — утверждений, принимаемых без доказательства, — из которых выводятся все теоремы и утверждения теории множеств. — Примеч. ред.