Ученые приблизились к пониманию псевдощели в высокотемпературных сверхпроводниках

Рис. 1. Схематическое изображение энергетического спектра вещества в нормальном (слева) и в сверхпроводящем состоянии. Валентная зона показана синим цветом, зона проводимости — красным. Взаимное пересечение (перекрытие) двух зон — фиолетовым. Куперовские пары (пара обведенных линией черных кружков) образуют основное (наиболее выгодное с энергетической точки зрения) состояние сверхпроводника. На энергетической шкале оно располагается в узкой области в окрестности уровня Ферми E_F. Остальные электронные состояния отделены энергетической щелью Δ. Пропорции не соблюдены, в реальности образованный куперовскими парами зазор очень узкий. Рисунок Юрия Ерина

Попытки выяснить, почему некоторые вещества становятся сверхпроводниками при относительно высокой температуре, а также что регулирует эту температуру, связаны с тщательным изучением разнообразных свойств и характеристик высокотемпературных сверхпроводников в нормальном и сверхпроводящем состоянии. Ученые из США, Японии и Таиланда провели серию экспериментов, в ходе которых им удалось существенно приблизиться к пониманию одного из самых загадочных свойств высокотемпературных сверхпроводников — наличия в них псевдощели.

В поисках возможности осознанного и направленного синтеза материалов, которые бы сверхпроводили при комнатной температуре, физикам приходится сталкиваться с промежуточными задачами, решение которых приближает к пониманию феномена высокотемпературной сверхпроводимости. Пожалуй, наиболее значимая из этих подзадач — выяснение причин возникновения и природы псевдощели в высокотемпературных сверхпроводниках (ВТСП).

В одном из последних выпусков журнала Science группа ученых из США, Японии и Таиланда опубликовала экспериментальную работу From a Single-Band Metal to a High-Temperature Superconductor via Two Thermal Phase Transitions, которая может помочь в поисках ответа на вопрос, что же такое псевдощель. Чтобы оценить результаты проведенных исследований, а также понять, чем данная работа выделяется среди множества других публикаций по псевдощелевой тематике, надо познакомиться с некоторыми ключевыми понятиями физики сверхпроводимости.

Энергетическая щель и псевдощель

Сверхпроводимость — это полное отсутствие электрического сопротивления и восприимчивости к внешнему магнитному полю (силовые линии не проникают внутрь материала). Это явление возникает в определенных веществах, когда их температура становится ниже критической. Критическая температура (T_c) — это характеристика, индивидуальная для каждого материала.

Несмотря на то что сверхпроводимость была открыта еще в 1911 году (см. Сверхпроводимость отмечает столетний юбилей, «Элементы», 08.04.2011), окончательная теория, объясняющая это явление, была создана только в 1957 году американскими физиками Джоном Бардиным, Леоном Купером и Робертом Шриффером. Она получила название «теория БКШ» по первым буквам фамилий ее создателей. Согласно теории БКШ, при температуре ниже T_c за счет квантов колебаний кристаллической решетки вещества, фононов, между электронами возникает притяжение, именуемое электрон-фононным взаимодействием. Поскольку электрон-фононное взаимодействие сильнее кулоновского отталкивания между электронами, электроны начинают объединяться в так называемые куперовские пары, которые ведут себя когерентным образом, то есть как единая квантовая система. Благодаря такому «единению» электроны проводимости без потерь энергии, а следовательно, и без сопротивления, могут протекать через кристаллическую решетку вещества.

Формирование куперовских пар приводит не только к изменению макроскопических характеристик вещества, таких как исчезновение электрического сопротивления или абсолютное непроникновение магнитного поля, но и к метаморфозам на микроскопическом уровне, а именно к модификации энергетического спектра материала.

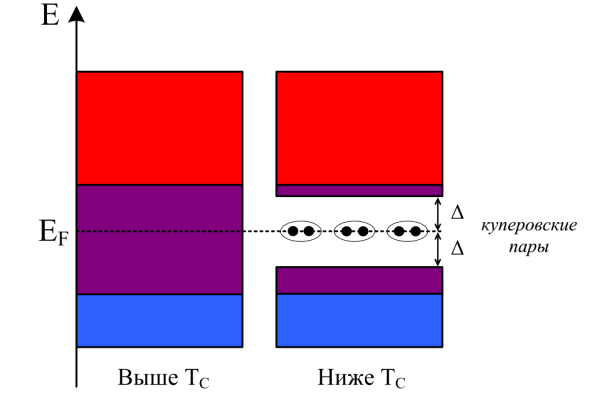
Что такое энергетический спектр? Еще из школьного курса известно, что электроны в атоме могут принимать только разрешенные значения энергии, располагаясь на определенных уровнях энергетической шкалы. Дискретный набор дозволенных уровней энергии атома называется его энергетическим спектром. В твердом теле таких атомов может быть огромнейшее количество. К тому же, они еще и взаимодействуют между собой. По этим причинам энергетические уровни каждого атома в твердом теле расщепляются на очень большое количество подуровней. Они расположены настолько близко друг к другу, что энергетический спектр атома перестает быть дискретным и становится практически непрерывным (или, как говорят, квазинепрерывным), образуя энергетическую зону. Для вещества, которое может стать сверхпроводником — а таковым может быть только вещество с металлической проводимостью, — энергетический спектр выглядит так, как это показано на рис. 1 слева.

В металле электроны с меньшими значениями энергии располагаются в валентной зоне, электроны с большей энергией — в зоне проводимости. Особенность энергетического спектра металла — перекрытие валентной зоны и зоны проводимости. Заметим, что в полупроводниках и изоляторах валентную зону и зону проводимости разделяет щель. Чем больше ее величина, тем сильнее выражены изолирующие свойства материала (см. рисунок из Википедии).

Как было сказано выше, электроны проводимости при температуре ниже критической начинают объединяться в куперовские пары. Однако, согласно теории БКШ, не все частицы задействованы в этом процессе, а лишь те, которые находятся вблизи определенного уровня энергии — так называемого уровня Ферми. Объединение в куперовские пары заканчивается тем, что в энергетическом спектре металла появляется симметричный относительно уровня Ферми разрыв — энергетическая щель (см. рис. 1, справа).

Может возникнуть вопрос: а как ведут себя носители заряда, которые находятся выше или ниже уровня Ферми? Так как суммарная энергия двух свободных электронов больше энергии куперовской пары, то они тоже стремятся сгруппироваться в пару и осесть на уровне Ферми. Чтобы разорвать куперовскую пару, необходимо затратить энергию, равную удвоенной величине щели (рис. 1). В свою очередь, величина энергетической щели определяется критической температурой. Поэтому чем больше T_c, тем больше энергии нужно затратить, чтобы пара электронов перестала существовать. Очевидно, что выше критической температуры энергетическая щель исчезает.

Заметим, что сверхпроводящая щель отличается от энергетических щелей в спектре полупроводников или диэлектриков. В случае диэлектрической или полупроводящей щели в ней вообще отсутствуют электроны, поскольку для них это своеобразное энергетическое «табу». В свою очередь, щель в спектре сверхпроводника просто отделяет равновесное состояние электронов (куперовские пары) на уровне Ферми от возбужденных частиц, которые могут находиться выше или ниже щели.

Довольно долго самыми «горячими» сверхпроводниками считались пленки германида ниобия Nb₃Ge c T_c = 22 К. Казалось, что это предел и теория БКШ не предусматривает веществ с большей критической температурой. Однако в 1986 году было обнаружено соединение La_2–xSr_xCuO₄ с критической температурой почти 40 К при х = 0,2 (х — степень допирования, то есть процент атомов, замененных атомами другого элемента или же просто убранных без какого-либо замещения). Так началась эра ВТСП на основе меди. В 2008 году монополия медных ВТСП была нарушена веществами на основе железа (см. Открыт новый тип высокотемпературных сверхпроводников, «Элементы», 12.05.2008).

Буквально за полгода ученые синтезировали материал YBa₂Cu₃O_7–δ (δ — всё та же степень допирования, только в данном случае показывающая «дефицит» по кислороду); его температура сверхпроводящего перехода достигала умопомрачительных для того времени 92 К. Анализ первых экспериментальных данных с ВТСП давал понять, что теория БКШ неспособна объяснять столь высокую T_c, хотя в то же время показывал, что в энергетическом спектре ВТСП имеет место щель, а электроны объединены в пары.

Вскоре ВТСП преподнесли своим исследователям новый сюрприз. При помощи различных экспериментальных методик было зафиксировано существование энергетической щели выше критической температуры. Не в силах дать какое-либо внятное объяснение такому феномену ученые назвали его «липовой» щелью, или псевдощелью. С этого момента и до сих пор не прекращаются попытки выяснить, что же представляет собой псевдощель и почему она образуется?

Было предложено несколько моделей. Одна из них утверждает, что куперовские пары не разрушаются при температуре выше T_c, они лишь теряют когерентность, то есть утрачивают между собой связь. Другая теория предполагает, что появление псевдощели выше температуры сверхпроводящего перехода обусловлено неким влиянием антиферромагнитного упорядочения ВТСП, которое возникает, когда он не допирован или слабо допирован носителями зарядов (например, для La_2–xSr_xCuO₄ носители заряда появляются из-за внедрения стронция, а в YBa₂Cu₃O_7–δ носители заряда и, соответственно, металлическая проводимость возникают благодаря аккуратному уменьшению δ, то есть «дефицита» по кислороду). В качестве доказательства этого сценария ученые приводят фазовую диаграмму вещества, демонстрирующую, как различные фазы материала с большой T_c меняются в зависимости от степени его допирования и температуры.

Рис. 2. Фазовая диаграмма состояния соединения Pb_0.55Bi_1.5Sr_1.6La_0.4CuO_6+δ (Pb-Bi2201) в зависимости от его температуры и уровня допирования носителями заряда δ (hole doping level). Черная область соответствует антиферромагнитной фазе вещества. Она возникает, когда материал слабо допирован или вообще не допирован носителями заряда. В кристалле Pb-Bi2201 уровень допирования δ определяется количеством атомов кислорода. Остальные фазы появляются при увеличении допирования: куполообразная синяя область ниже T_c задает сверхпроводящую область, загадочная псевдощелевая фаза — красная область. T* определяет температуру, при которой появляется псевдощель. Белая область — это нормальное металлическое состояние Pb-Bi2201. На вставке вверху показана кристаллическая решетка Pb-Bi2201. Зеленая полоса и стрелка обозначают направление, вдоль которого авторы обсуждаемой статьи наблюдали температурную эволюцию энергетического спектра вещества, его магнитную структуру и оптические свойства. См. подробности в тексте. Рисунок с сайта newscenter.lbl.gov

На рис. 2 приведена одна из типичных диаграмм состояния ВТСП со сложной химической формулой Pb_0.55Bi_1.5Sr_1.6La_0.4CuO_6+δ, которая сокращенно обозначается Pb-Bi2201. Видно, что сверхпроводимость в нём наблюдается лишь в определенных интервалах допирования (эта область отмечена синим цветом), при этом наибольшая T_c (приблизительно 38 К) достигается, когда δ = 0,15. Образец с максимально возможной для него критической температурой в литературе называют оптимально допированным. Меньший уровень допирования (недодопированный образец) превращает исходное вещество в антиферромагнетик и изолятор (черная область на диаграмме). Псевдощелевая фаза, которая наступает при температуре T*, показана на рисунке как красная область. Фактически она расположена как раз между антиферромагнитной и сверхпроводящей фазой ВТСП. Именно такое соседство, как полагают ученые, обуславливает рождение псевдощели.

К высокотемпературной сверхпроводимости через два фазовых перехода

Псевдощелевое состояние в Pb-Bi2201 и стало объектом исследований авторов публикации в Science. Может возникнуть вопрос: почему из множества других медных ВТСП ученые сосредоточили свое внимание именно на этом материале? Главная причина такого выбора связана с большим температурным интервалом перехода от псевдощелевого состояния к сверхпроводящему в оптимально допированном образце. Широкий температурный коридор (зеленая полоса со стрелкой на рис. 2) позволяет неспешно пронаблюдать эволюцию энергетического спектра Pb-Bi2201 и заодно попытаться прояснить природу псевдощели.

Ученые приготовили серию кристаллов Pb-Bi2201, а затем подвергли их исследованию с помощью различных методик, которые отображают желаемый энергетический спектр, а также другие характеристики, помогающие идентифицировать псевдощелевое состояние.

Наиболее распространенная методика обнаружения псевдощели — фотоэмиссионная спектроскопия с угловым разрешением (ARPES). В ARPES поверхность исследуемого образца облучается рентгеновскими лучами, которые выбивают из валентной зоны электроны. По энергии и направлению вылетевших валентных электронов определяется энергетический спектр материала. При помощи ARPES авторы статьи обнаружили, что псевдощель в оптимально допированном кристалле рождается при температуре около 132 К. Этот результат согласуется с измерениями, проведенными другими учеными, так что ничего удивительного в этом пока нет.

Фотоэмиссионная спектроскопия с угловым разрешением — безусловно, эффективная для своего круга проблем технология, однако она дает лишь поверхностную (в буквальном смысле) информацию о веществе. Для поставленной задачи этого явно недостаточно, поэтому ученые решили привлечь методики, которые могли бы заглянуть внутрь вещества и проследить, как меняется внутренняя структура и свойства кристаллов в окрестности температуры появления псевдощели и происходят ли эти изменения в Pb-Bi2201 при температуре T* = 132 К.

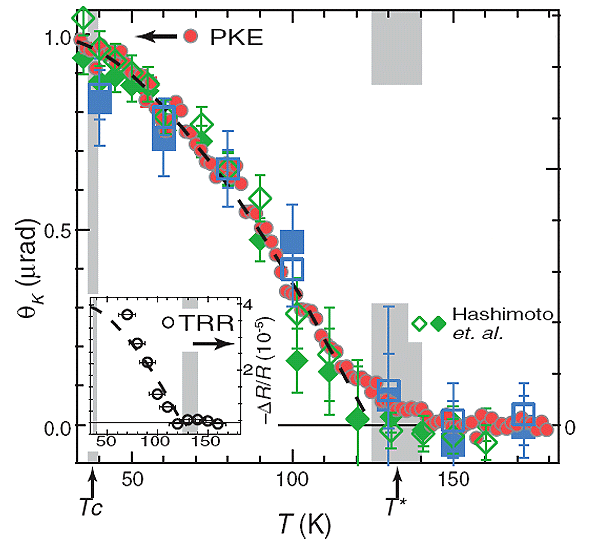
Для этого ученые обратились к измерениям в исследуемом веществе магнитооптического эффекта Керра — влияния намагниченности среды на поляризацию отраженного от нее света. Магнитное поле внутри кристалла приводит к вращению плоскости поляризации отраженного света (плоскости, задаваемой вектором напряженности электрического поля и вектором, указывающим направление распространения электромагнитной волны). Это вращение пропорционально намагниченности кристалла. Применительно к Pb-Bi2201 магнитооптический эффект Керра возникал, когда температура становилась меньше 132 К (рис. 3), то есть ниже T*. И хотя угол вращения совсем маленький, порядка микрорадиана, ясно, что при этой температуре внутри кристалла происходит изменение магнитного порядка. А при температуре выше T* никакого угла не возникает.

Этот факт, а также то, что появление ненулевого угла вращения очень точно совпадает по температуре с возникновением псевдощели, навело авторов статьи на следующую мысль: псевдощелевая фаза — это независимое от сверхпроводимости состояние, никак не связанное с «отголосками» сверхпроводящей фазы в виде некогерентных куперовских пар. Более того, появление псевдощели нужно идентифицировать как полноценный фазовый переход в веществе, такой же, как, например, переход к сверхпроводимости.

Рис. 3. Температурная зависимость угла вращения Θ_K (в микрорадианах) плоскости поляризации в магнитооптическом эффекте Керра (PKE — polar Kerr effect) для Pb-Bi2201. T* обозначает температуру возникновения ненулевого угла вращения, которая затем идентифицируется авторами как температура наступления псевдощелевого состояния, T_c — температура сверхпроводящего перехода. Красные круги соответствуют экспериментальным данным авторов статьи. Зеленые ромбы и голубые квадраты представляют аналогичные результаты по магнитооптическому эффекту Керра, взятые их других работ. Пунктирная черная линия проведена для лучшего восприятия измеренных данных. На вставке: температурная зависимость изменения коэффициента отражения, полученная при помощи спектроскопии временного разрешения (TRR — time-resolved reflectivity). Изображение из обсуждаемой статьи в Science

Чтобы проверить справедливость своей гипотезы о фазовом переходе, авторы статьи применили еще одну методику — спектроскопию временного разрешения (time-resolved spectroscopy). Данная технология является довольно распространенным способом измерения характеристик ВТСП, позволяя в реальном времени проследить за поведением электронов внутри материала при фазовом сверхпроводящем переходе, а также измерить величину сверхпроводящей щели и псевдощели. Спектроскопия временного разрешения представляет собой детектирование кратковременного изменения (в пределах пикосекунды, 10^–12 с) коэффициента отражения света, вызванного фемтосекундными (10^–15 с) лазерными импульсами линейно поляризованного света. Результаты обрабатываются специально созданной теорией, из которой можно извлечь желанные данные по веществу (динамику куперовских пар вблизи T_c, щель и псевдощель).

Применив данную технологию к Pb-Bi2201, ученые обнаружили, что, когда температура образца составляет опять-таки те же 132 К, рождается ненулевой сдвиг в значении коэффициента отражения кристалла, который при понижении температуры монотонно увеличивается. Интересно, что такой же по характеру сдвиг в значении коэффициента отражения наблюдается, когда Pb-Bi2201 становится сверхпроводником. Конечно, это изменение довольно маленькое, порядка 10^–5, как можно видеть из графика на рис. 3. Тем не менее оно есть, что лишний раз доказывает правильность гипотезы, высказанной авторами.

Итак, выходит, что три разных экспериментальных методики указывают на то, что появление псевдощели при температуре приблизительно 132 К нужно воспринимать не иначе как фазовый переход. Таким образом, чтобы кристалл ВТСП начал сверхпроводить, он по мере понижения температуры должен испытать два фазовых перехода: сначала появление псевдощели, а затем рождение сверхпроводимости.

В своей статье ученые не дают ответа на вопрос о причинах возникновения псевдощели, однако то, что псевдощель оказалась совершенно обособленным состоянием вещества, не имеющим к сверхпроводимости никакого отношения, — несомненно, очень важный результат для дальнейших исследований в псевдощелевой тематике.

Источник: Rui-Hua He, M. Hashimoto, H. Karapetyan, J. D. Koralek, J. P. Hinton, J. P. Testaud, V. Nathan, Y. Yoshida, Hong Yao, K. Tanaka, W. Meevasana, R. G. Moore, D. H. Lu, S.-K. Mo, M. Ishikado, H. Eisaki, Z. Hussain, T. P. Devereaux, S. A. Kivelson, J. Orenstein, A. Kapitulnik, Z.-X. Shen. Two Thermal Phase Transitions From a Single-Band Metal to a High-Temperature Superconductor via Two Thermal Phase Transitions // Science (2011). V. 331. P. 1579–1583.

Юрий Ерин