Столкновение твердого тела с жидкостью может генерировать сверхзвуковой воздушный поток
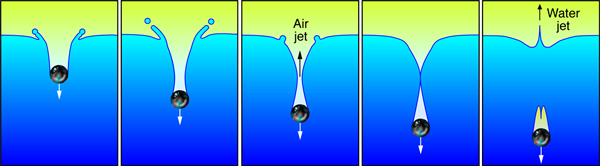
Известно, что при падении твердого тела в жидкость возникает воздушная полость, которая под действием гидростатического давления спустя некоторый промежуток времени схлопывается, образуя характерный всплеск. Эксперименты по столкновению тонкого диска с поверхностью воды, проведенные группой голландских и испанских физиков, и последующее численное моделирование указывают на то, что воздушная полость дополнительно создает еще и сверхзвуковую струю воздуха, которая может вытекать из полости со скоростью около 580 м/с.
Столкновение твердого тела с ровной поверхностью жидкости рождает последовательность нетривиальных событий, являющихся предметом активного интереса ученых на протяжении уже более ста лет. В 1908 году была издана книга «Splash of a drop» английского физика Артура Уортингтона. В своей книге он впервые подробно исследовал и описал процесс столкновения твердого тела с жидкой средой. Если попытаться кратко изложить это явление, происходит следующее (см. рис. 1): сталкивающийся объект образует в жидкой среде полость с вертикальной осью симметрии, которая, благодаря гидростатическому давлению, начинает схлопываться, что приводит к образованию воздушного перешейка (или сужения) и в конечном итоге — к отсечке стенками жидкости воздушной полости. Далее из точки, где воздушная полость отсекается, выбрасываются вверх и вниз две очень тонкие струи — струи Уортингтона.
Год назад «Элементы» рассказывали о публикации группы голландских и испанских физиков, построивших по результатам своих экспериментов теоретическую модель, объясняющую экстремально малую толщину струй Уортингтона. Теперь эта же коллаборация обнаружила необычный эффект, который возникает при падении тела в жидкость. Оказывается, схлопывающаяся воздушная полость создает струю воздуха, которая имеет скорость, близкую к скорости звука. Более того, в самый последний момент, перед тем как воздушная полость отсекается жидкостью, скорость вытекающего из нее воздуха значительно превосходит даже скорость звука, то есть исходящий из полости поток воздуха становится сверхзвуковым. Результаты своих экспериментальных и теоретических исследований ученые опубликовали в статье Supersonic Air Flow due to Solid-Liquid Impact в журнале Physical Review Letters (полный текст доступен здесь, PDF, 472 Кб).
Экспериментальная установка состояла из тонкого круглого диска радиусом 2 см. К центральной части его нижней стороны был прикреплен тонкий стержень, с помощью которого имитировалось падение диска с постоянной скоростью 1 м/с. Чтобы визуализировать, как воздух вытекает из образующейся воздушной полости, ученые использовали микроскопические (3 мкм) капельки глицерина. Эти капельки создавали над поверхностью воды дымовую завесу, которая затем увлекалась диском при его вхождении в жидкость. В распоряжении исследователей также находилась высокоскоростная камера, способная записывать видео со скоростью 15 000 кадров в секунду. На рис. 2 показаны три снимка, полученные с помощью такой камеры.

Поскольку технология, используемая авторами статьи, не позволяла им измерить скорость струи воздуха при дальнейшем сближении водяных стенок полости, они прибегли к численному моделированию динамики воздушного потока с помощью уравнений Эйлера. Графики на рис. 3 иллюстрируют результаты их расчетов, а именно — зависимости давления внутри воздушной полости pcav и скорости воздушной струи uneck, текущей через перешеек полости, от его радиуса rneck. Из графиков следует, что, когда радиус перешейка составляет около 0,5 мм, скорость струи через сужение достигает 330 м/с, то есть скорости звука. Такая скорость струи возникает за счет того, что давление воздуха внутри полости на 0,02 атмосферы больше окружающего. Удивительно, но такой небольшой разницы давлений оказалось достаточно, чтобы заставить воздух двигаться через сужение со скоростью звука.

Чтобы удостовериться в правильности своих вычислений, ученые на теоретическую кривую зависимости uneck от rneck наложили аналогичную экспериментальную зависимость (вставка на рис. 3). Явное согласие экспериментально полученных точек (черные ромбы) и сплошной теоретической кривой (красного цвета) указывало, по мнению ученых, на правильность их теоретической модели.
Далее авторы статьи решили определить более точно радиус перешейка, при котором воздух начинает течь через него со звуковой скоростью. Для этого они рассчитали эволюцию числа Маха (отношение скорости воздушной струи через сужение к скорости звука) в зависимости от радиуса перешейка для скорости диска 1 и 2 м/с (рис. 4).

Выяснилось, что, как только радиус перешейка уменьшается до 0,5 мм для меньшей скорости и 1,2 мм для большей, число Маха равно 1 — что означает, что воздух протекает через перешеек со скоростью звука.
Однако в названии обсуждаемой статьи употребляется выражение «сверхзвуковое течение воздуха» (supersonic air flow). Возникает вопрос: так где же в полости воздух течет со сверхзвуковой скоростью?
Если внимательно присмотреться к графикам на рисунках 3 и 4, можно увидеть, что расчетные кривые заканчиваются, когда радиус перешейка составляет 0,5 мм (для скорости диска 1 м/с), что соответствует скорости воздушного потока приблизительно 330 м/с. Дальнейший численный анализ установил, что скорость больше скорости звука воздушная струя приобретает, как только она миновала перешеек.

На рис. 5 показано распределение чисел Маха (Ma) воздушной струи вдоль вертикальной оси симметрии полости на участке, ограниченном верхним синим прямоугольником, когда радиус перешейка менялся от 0,9 мм (кривая 1) до 0,5 мм (кривая 5). Легко видеть, что максимальное значение Ма для области воздушного потока, расположенной чуть выше перешейка с радиусом 0,5 мм (местоположение перешейка на графике указано пунктирной линией) равно 1,75 (кривая 5). Вспомнив определение числа Маха, несложно посчитать, что струя воздуха в этот момент и в этой области двигается со скоростью почти 580 м/с.
Таким образом, сверхзвуковое течение воздуха, согласно численному моделированию, должно наблюдаться в узкой области сразу над перешейком буквально перед самым его исчезновением. Такое поведение воздушной полости в воде напоминает сопло Лаваля — специальную конструкцию, предназначенную для ускорения проходящего через него газового потока до сверхзвуковых скоростей.
Источник: Stephan Gekle, Ivo R. Peters, José Manuel Gordillo, Devaraj van der Meer, Detlef Lohse. Supersonic Air Flow due to Solid-Liquid Impact // Phys. Rev. Lett. 104, 024501 (2010).
Юрий Ерин
-
В статье упоминается, что форма полости очень напоминает сопло Лаваля. Кто не знает, расскажу, что сопло Лаваля представляет собой канал с меняющимся по длине площадью поперечного сечения, комбинацию конфузора и дифузора. Самое узкое место называется критическим сечением.
Чтобы понять, как работает сопло Лаваля, нужно сперва представить себе, как работает обычное сужающееся сопло( просто мысленно отбросить диффузор). Чтобы газ начал течь через сопло, необходимо, чтобы давление на входе было больше, чем на выходе. Отношение давлений называют перепадом. Газ, двигаясь по сужающемуся соплу, расширяется. Чем больше перепад, тем больше скорость истечения....пока перепад не достигнет критического значения. При критическом значении перепада скорость газа в критическом сечении равно скорости звука.
Дальнейшее увеличение перепада не приводит к увеличению скорости истечения. Оно равно скорости звука и не увеличивается. Чтобы увеличить скорость потока, движущегося со звуковой скоростью, его нужно направить через расширяющийся канал.
Таким образом, сопло Лаваля создает струю газа, истекающего из него со сверхзвуковой скоростью при следующих условиях:
1) Перепад должен быть сверхкритическим.
2) Скорость газа в критическом сечении долна быть звуковой. -
Особо не вникал, но я так понимаю что газ при таких течениях испытывает адиабатическое расширение и охлаждение. И не мудрено, внутренняя тепловая энергия хаотического движения молекул переходит в энергию упорядоченного течения газа. При истечении-охлаждении скорость звука резко падает - молекулы-то как двигались, так и движутся приблизительно со звуковой скоростью, но вот относительные скорости соседних молекул в быстром потоке оказываются не велики, т.к. все молекулы движутся в одном направлении строем. Так что не скорость потока обгоняет скорость звука, а уместней сказать, что в сопле Лаваля скорость звука падает ниже скорости потока. Если газ достаточно расширять, то его можно охладить до сколь угодно низкой температуры, но скорость истечения при этом в бесконечность не уйдёт. Про это как-то не было сказано ни слова - почему? Или я где-то что-то напутал?
Как итог сказанного, "Вспомнив определение числа Маха, несложно посчитать, что струя воздуха в этот момент и в этой области двигается со скоростью почти 580 м/с" - не верно, т.к. множить надо на ЛОКАЛЬНУЮ скорость звука, которая будет меньше чем общепринятая 330м/c; а насколько меньше - не ясно.-
Ну скорость звука посчитать несложно. Это sqr(k*R*T).
Здесь k - показатель политропы(для воздуха k=1.4)
R - универсальная газовая постоянная
T - температура в кельвинах.
В ваших рассуждениях Вы допустили две ошибки. Первая. Упорядоченное движение в сопле возникает только при наличии перепада, то есть разницы давлений на входе и на выходе. Естественно, при расширении газ охлаждается, но причиной движения внутренняя энергия газа не является.
А вторая Ваша ошибка заключается в том, что истечение происходит не в вакуум, а в воздушную среду с нормальным давлением и температурой. Следовательно, бесконечно расширяться газ не может - внешнее давление этому воспрепятствует. (Именно поэтому для ракетных двигателей в технических характеристиках указывают два значения тяги: в пустоте и на уровне моря.) -
Локальная скорость звука - это скорость звука в ОКРУЖАЮЩЕЙ движущийся воздух среде, т.е. воздух, который в движении не участвует.
На счёт адиабатического истечения воздуха из полости, то не стоит думать, что там температура падает очень сильно. В статье показано (и об этом сказано в новости), что давление воздуха внутри полости имеет максимум 1,02 атмосферы, снаружи - 1 атм. Из уравнения Пуассона можно посчитать падение температуры вытекающей струи - оно будет очень и очень незначительным, около 1 К.-
"Локальная скорость звука - это скорость звука в ОКРУЖАЮЩЕЙ движущийся воздух среде" - вот это тезис, который мне очень сложно принять. А если вокруг будет вакуум? В сопле Лаваля, если оно используется правильным образом, на его критическом сечении (самое узкое место) скорость потока равна именно скорости звука конкретно в том веществе, что там и течет, и не важно что вокруг. Про 1К поверю, т.к. сам считать не умею. Тем не менее, мне не ясно, откуда берётся энергия, позволяющая продолжать разгонять воздух сверх скорости звука, причем столь существенно. По моим интуитивным представлениям такое возможно лишь при значительном расширении (на расширяющейся части сопла Лаваля).
-
Если бы инженеры при проектировании летательных аппаратов руководствовались только интуицией - уверяю вас, до сих пор самолеты бы оставались такими, какими были сто лет назад, когда Уилбур Райт совершил первый полет длительностью чуть больше минуты. По сути,первый самолет - это планер Шанюта с установленным на него автомобильным движком от форда. После этого интуиция, хоть и осталась в авиастроении, все же уступила место точному расчету и многочисленным продувкам в аэродинамических трубах.
Посмотрите на графики в статье. Хорошо видно, как там растет давление в пузыре в результате схождения его стенок. Это давление и является источником энергии, которое разгоняет газ в сопле Лаваля. -
Говоря в конце новости о воздушной полости как о сопле Лаваля я имел в виду лишь приблизительную аналогию. Сопло Лаваля имеет жёсткую недеформируемую конструкцию, оно не изменяет свои размеры при вытекании из него газа в отличие от воздушной полости и её перешейка, которые постоянно меняют кривизну своей формы. Что математически означает непостоянство кривизны? Газодинамика сопла Лаваля и воздушной полости с её перешейком рассчитывается из уравнения Эйлера,но только в последнем случае начинают учитываться дополнительные слагаемые в уравнение Эйлера, которые учитывают непостоянство кривизны и которые начинают сильно сказываться в тот момент, когда перешеек совсем тонкий.
Действительно, как сказано постом выше, посмотрите на график на рисунке 3b в статье. Там показана зависимость давления воздуха в перешейке от его размера. Видно, что когда сужение очень тонкое, то давление там падает до 0,6 атм. Таким образом воздух из полости втягивается в нестационарный перешеек, а затем это сужение как бы выплёвывает из себя этот втянутый воздух, и сразу за перешейком скорость воздуха возрастает. Теперь отвечу на Ваш вопрос относительно откуда энергия? Это разность давлений в воздушной полости и перешейке и постоянно изменяющаяся кривизна этого перешейка. Причём, не весь воздух в полости участвует в сверхзвуковом движении, а лишь очень незначительная его часть. Посмотрите на рисунок 5 новости, где приведен профиль распределения скоростей выше перешейка, он очень острый. Это к тому, что для разгона до сверхзвуковой скорости не требуется уж так много энергии, как Вы, возможно, думаете.
В самой статье авторы подразумевают скорость звука в этой "системе" ИМЕННО 330 м/с, т.е. они не заморачиваются определением числа Маха. Это я уже отсебятину добавил с приблизительным значением скорости воздуха.
Если отвлечься от этой статьи, то учёных в процессе решения уравнения Эйлера особо не заботит численное значение локальной скорости звука. Они как бы загоняют его в это уравнение и потом следят за эволюцией не локальной скорости звука, а числа Маха. Если число Маха оказывается больше 1, то значит имеем сверхзвуковое течение. Какое численно значение скорости звука в этот момент, учёных особо не волнует.
Ваши сомнения относительно локальной скорости звука мне понятны. Но из-за того, что температура воздушного потока меняется очень слабо, то скорость звука остаётся фактически неизменной.-
В общем с чем-то разобрался. Но я как математик по образованию категорически не переношу такого вольного отношения к определениям, в т.ч. "числа Маха".
Про локальную скорость звука: а может и падает, кто его знает. Температура падает всего на 1К на выходе из сопла, но на сверхзвуковом участке возможно и ниже, если где-то давление падает локально до 0,6 атм. Но это так, к слову - чтоб идущие следом при решении подобных задач не зевали.
-
-
-
-
Заинтересованным рекомендую ознакомится с рвботами Седова, Логвиновича Они довольно хорошо использовали аппарат общих принципов механики для описаноя процессов происходящих при входе в воду, в том числе и с большими скоростями. Ученые филиала ЦАГИ (Москва) в этом направлении много сделали.
Последние новости