Впервые удалось увидеть уровни Ландау в графене

Рис. 1. Зонная структура твердого тела

Квантовомеханические расчеты показывают, что магнитное поле, приложенное к проводнику, заставляет электроны проводимости — заряженные частицы, которые участвуют в переносе электрического тока, — двигаться с некоторой скоростью по замкнутым орбитам с дискретным и равномерно распределенным набором значений энергий. Такие проквантованные орбиты называются уровнями Ландау. В графене уровни Ландау распределены неравномерно, поскольку электроны проводимости ведут себя в нём как безмассовые частицы — скорость их движения не зависит от их энергии. Группе американских ученых удалось впервые экспериментально зафиксировать уровни Ландау в графене. Полученные результаты прекрасно согласуются с теоретическими предсказаниями.

Двумерная форма углерода, графен, представляет интерес не только из-за перспектив использования в наноэлектронике, но и благодаря некоторым необычным эффектам, относящимся к фундаментальной науке. Например, целочисленный и дробный квантовый эффект Холла в графене ведет себя совсем не так, как в остальных веществах (о квантовом эффекте Холла см. статьи в Соросовском образовательном журнале: Е. Н. Бормонтов «Квантовый эффект Холла», PDF, 143 Кб и О. В. Кибис «Квантовый эффект Холла», PDF, 107 Кб). Уникальность физических свойств графена обусловлена необычным, релятивистским, законом дисперсии квазичастиц, которые переносят электрический ток.

Прежде чем перейти к изложению новости, совершим небольшой экскурс по основным положениям так называемой зонной теории твердого тела, поскольку для дальнейшего понимания необходимо иметь представление о квазичастицах, законе дисперсии квазичастиц и, собственно, об уровнях Ландау.

Как возникает электрический ток. Зонная теория твердого тела

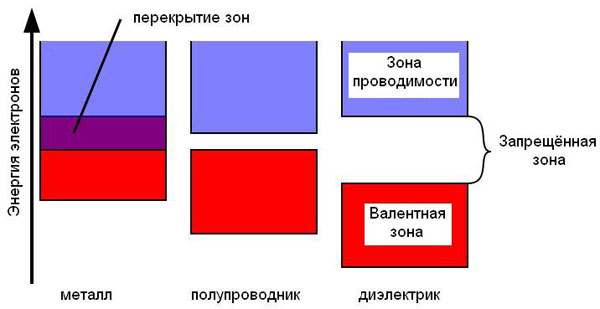
Общеизвестно, что в подавляющем большинстве твердых тел электрический ток обусловлен движением электронов (о случаях, когда это не так, см., например, новость Обнаружена суперионная проводимость в фуллериде лития, «Элементы», 23.04.2009). Такие электроны называются электронами проводимости. Они появляются во внешних, удаленных от ядра областях атома. Эти области формируют в твердом теле валентные зоны. Чтобы возник электрический ток, электроны должны из валентной зоны взобраться выше по энергетической шкале и перейти в зону проводимости, преодолев при этом зону запрещенных значений энергии, или запрещенную зону. Если все три упомянутые зоны разместить по оси энергии, то зона с меньшей энергией будет валентной, далее идет запрещенная зона и потом зона с наибольшей энергией — зона проводимости (рис. 1).

Как валентная зона, так и зона проводимости представляют собой очень плотную упаковку из множества доступных для электронов дискретных уровней энергии — энергетических «изолиний». Эти уровни расположены так близко друг к другу, что практически сливаются в непрерывную полосу, которая и называется энергетической зоной. Напротив, в запрещенной зоне доступных для электрона энергетических уровней вообще нет, и электроны там находиться не могут. Итак, чтобы возник электрический ток, необходимо, чтобы электроны из валентной зоны перескочили через запрещенную зону и попали в зону проводимости.

Как известно из школьного курса физики, вещества, в зависимости от того, как они проводят электрический ток, можно разделить на металлы, полупроводники и диэлектрики. С точки зрения зонной теории металлы — это твердые тела, у которых запрещенная зона отсутствует, вместо нее наблюдается сильное перекрытие валентной и проводящей зон. Получается, что электронам в металле нет необходимости тратить энергию на преодоление запрещенной зоны, а потому под внешним воздействием — в электрическом поле — они легко переходят в зону проводимости. Отсюда легко понять, почему металлы — хорошие проводники.

В диэлектриках ширина запрещенной зоны значительно больше тепловой энергии электронов даже при комнатной температуре, а значит, подавляющее большинство потенциальных носителей тока не могут перепрыгнуть в зону проводимости — им не хватает энергии. Преодоление запрещенной зоны может произойти лишь при очень сильных полях (тогда наблюдается электрический пробой диэлектрика) или очень высоких температурах.

И наконец, если ширина запрещенной зоны сравнима с энергией теплового движения электронов, то мы имеем полупроводник. Повышение температуры экспоненциальным образом увеличивает количество электронов, прыгающих через запрещенную зону в зону проводимости.

Что такое квазичастицы. Закон дисперсии квазичастиц

Электроны в твердых телах движутся в периодическом электрическом поле, которое создается ионным остовом кристаллической решетки твердого тела. Естественно, этот остов оказывает некоторое влияние на движение и поведение электронов — благодаря этому происходит образование вышеописанной зонной структуры твердого тела. Воздействие остова заключается еще и в том, что электроны при движении по твердому телу приобретают эффективную массу, которая уже не равна их массе покоя: она может быть меньше, а может и больше массы покоя. Поэтому электроны в твердом теле называют квазичастицами, то есть «почти» электронами.

Дальнейшее развитие зонной теории, в частности исследование эффекта Холла, показало, что перенос электрического тока можно описывать не только с помощью отрицательно заряженных квазичастиц — «почти» электронов, но и при помощи положительно (!) заряженных квазичастиц. Такие квазичастицы назвали «дырками». Сразу оговоримся, что в реальности электрический ток несут именно электроны, а введение дырок вызвано стремлением учесть некоторые экспериментально наблюдаемые факты. Таким образом, в некоторых случаях удобно считать, что ток переносится не электронами (отрицательно заряженными квазичастицами), а фиктивными квазичастицами с положительным зарядом (дырками), заполняющими все те дискретные уровни в зоне проводимости, которые не заняты электронами.

Важно понимать, что для одной и той же зоны нельзя пользоваться одновременно двумя способами описания. Если электрический ток переносят отрицательно заряженные квазичастицы (электроны), то незаполненные уровни не вносят в него никакого вклада; если же носителями тока являются дырки, то тогда нет вклада от электронов. Тем не менее в зонной теории допустимо одни зоны описывать «дырочным» языком, а другие с помощью электронов. Выбор описания зависит от удобства. Например, электроны, покинувшие валентную зону и перешедшие в зону проводимости, оставляют на своих местах дырки. Поэтому описывать зону проводимости можно в терминах электронов, а валентную зону — в терминах дырок.

Зонную теорию твердого тела можно проиллюстрировать простой аналогией. Представим себе ряд кресел в кинотеатре, заполненный зрителями. Кто-то в середине ряда хочет пересесть подальше — для этого он перепрыгивает через спинку кресла в следующий, пустой, ряд. Пустой ряд — это зона проводимости, а человек, который пересел, — электрон.

Теперь в этом ряду появилось свободное место. Представим, что еще один человек хочет сесть в этот почти заполненный ряд. Он стоит у края ряда, ближайшее кресло занято, а свободное место находится далеко от него. Люди, сидящие в этом ряду, начинают сдвигаться по одному, приближая таким образом свободное место к ожидающему его человеку. Можно сказать, что свободное место перемещается. Как только свободное место достигнет края ряда, где находится человек, он сможет сесть. Если вообразить, что люди, сидящие в этом ряду, отрицательно заряжены (как электроны), а свободные места — носители положительного заряда, то описанное движение людей соответствует электронной проводимости, а движение свободных мест — дырочной.

Зависимость энергии квазичастиц от импульса при движении в зоне проводимости называют законом дисперсии. В металлах закон дисперсии можно с хорошей точностью считать квадратичным, то есть энергия квазичастиц прямо пропорциональна квадрату импульса. Такую аппроксимацию называют приближением свободных электронов, и она дает почти полное согласие с экспериментальными данными по характеристикам твердых тел (теплопроводность, удельное сопротивление и т. д.). Почему «почти»? Да потому что воздействие периодического потенциала кристаллической решетки в металлах хоть и невелико, но совсем свободными электроны (квазичастицы) в них назвать всё-таки нельзя.

А как же устроена проводимость у графена? Его нельзя отнести ни к металлам, ни к полупроводникам, ни, тем более, к диэлектрикам. Графен — полуметалл (не единственный, к такому классу веществ принадлежат еще бор, кремний, германий, мышьяк, полоний, графит — родитель графена — и др.). Исходя из зонной теории, графен — это вещество, у которого валентная зона и зона проводимости перекрываются (запрещенная зона отсутствует, как в металлах), но, в отличие от тех же металлов, это пересечение очень мало. Точки соприкосновения зоны проводимости и валентной зоны в графене называют точками Дирака. В этих точках закон дисперсии квазичастиц имеет линейный вид: энергия квазичастиц прямо пропорциональна их импульсу.

И вот здесь начинается самое любопытное. Подобной зависимостью энергии от импульса обладают еще и безмассовые частицы — фотоны. Получается, что реальные частицы — электроны — в графене ведут себя как фотоны, то есть имеют нулевую массу и их энергия не зависит от скорости движения. Именно поэтому закон дисперсии квазичастиц в графене именуют релятивистским. Однако, в отличие от фотонов, электроны в графене еще и обладают зарядом (и полуцелым спином, то есть являются фермионами), поэтому квазичастицы графена называют также дираковскими фермионами. Среди известных в настоящее время веществ нет аналогов с подобным «графенным» законом дисперсии.

Уровни Ландау в графене

Теперь наконец можно перейти к рассказу об уровнях Ландау. Представим себе двумерный проводник с квадратичным законом дисперсии. Поместим этот проводник в перпендикулярное его поверхности внешнее магнитное поле. Лев Давидович Ландау в 1930 году показал, что квазичастицы в таком проводнике будут двигаться по замкнутым орбитам с частотой, зависящей от индукции магнитного поля. Энергия такого движения — закон дисперсии — квантуется (то есть дискретна) и пропорциональна некому целому числу n, обозначающему номер орбиты или уровня. Множество таких замкнутых орбит называют уровнями Ландау. Можно сказать, что закон дисперсии для квазичастиц в магнитном поле и уровни Ландау — одно и то же. Расстояние по энергетической шкале между соседними орбитами одинаковое, или, как говорят физики, уровни Ландау эквидистантны. Заметим также, что в случае нулевого уровня (n = 0) энергия электронов не становится равной нулю.

Рис. 2. Схематическое изображение закона дисперсии квазичастиц в графене в магнитном поле, или уровней Ландау для электронов (синие окружности) и дырок (коричневые окружности). Энергия каждого уровня отсчитывается от энергии в дираковской точке E_D — точке соприкосновения валентной и проводящей зон (см. пояснения в тексте). Рис. из обсуждаемой статьи в Science

А как зафиксировать уровни Ландау в реальном эксперименте? Оказывается, квантование Ландау приводит к возникновению как минимум двух явлений: эффекта де Гааза—ван Альфена и эффекта Шубникова—де Гааза. Первый заключается в осцилляциях намагниченности материала в сильном магнитном поле (порядка 1 Тл) при температурах жидкого гелия, второй — в осцилляциях проводимости при тех же условиях. Низкая температура и сильное магнитное поле позволяют избежать значительного влияния температуры на обнаружение квантования Ландау. В этих эффектах пики на осцилляциях физических величин и есть признак того, что произошло образование уровней Ландау.

В графене, из-за линейности закона дисперсии, уровни Ландау квантуются совершенно иначе. Во-первых, энергия квазичастиц в графене зависит от номера орбиты как √n, поэтому уровни Ландау в нём не эквидистантны (рис. 2), и во-вторых, при n = 0 энергия квазичастиц в графене равняется нулю даже в присутствии магнитного поля.

До сих пор не было четкого подтверждения этих особенностей квантования Ландау в графене. И вот сравнительно недавно группе американских ученых из Физической школы Технологического института Джорджии (Антанта, США) совместно с коллегами из Центра наноразмерных систем и технологий Национального института стандартов и технологий (Гейтерсберг, Мэриленд, США) удалось пронаблюдать около 20 уровней Ландау в графене. Их статья Observing the Quantization of Zero Mass Carriers in Graphene опубликована в журнале Science.

Графен был выращен на подложке из карбида кремния SiC. В отличие от традиционного «фундамента» для получения графена  (из оксида кремния), использование SiC позволяло избежать ненужного влияния подложки на дальнейшие измерения. Фиксирование уровней Ландау в обсуждаемой работе происходило с помощью эффекта Шубникова—де Гааза. Подавая напряжение на исследуемый образец, ученые измеряли его проводимость в присутствии сильного магнитного поля при температуре 4,3 К. Результат одного из таких измерений — в магнитном поле с индукцией 5 Тл — показан на рис. 3.

Рис. 3. Непосредственное измерение квантования Ландау в графене во внешнем магнитном поле 5 Тл. На графике приведена зависимость проводимости графена (в наносименсах) от прикладываемого к нему напряжения (в мэВ). Экспериментально полученные данные показаны синими точками. Красная кривая — интерполяция экспериментальных результатов. Каждый всплеск на осциллирующей кривой соответствует уровню Ландау (нумерация указана на кривой). Рис. из обсуждаемой статьи в Science

По оси абсцисс отложено прикладываемое напряжение в энергетических единицах (мэВ), по оси ординат — измеренная проводимость графена (в наносименсах). Ярко выраженные пики на приведенной осциллирующей зависимости свидетельствуют о том, что экспериментаторы наблюдают уровни Ландау. На этом графике видна и неэквидистантность расположения уровней Ландау, но, чтобы окончательно удостовериться в их неравномерном расположении, авторы построили также зависимость величины энергии квазичастиц на каждом из уровней Ландау от их порядкового номера n (рис. 4) для различных значений индукции внешнего магнитного поля.

Рис. 4. Энергия n-го уровня Ландау как функция квадратного корня из произведения индукции внешнего магнитного поля B и порядкового номера уровня n. Прямая линия указывает на прекрасное согласие экспериментальных данных по дисперсии квазичастиц с теоретическим законом. Рис. из обсуждаемой статьи в Science

Прямая линия на графике свидетельствует об очень хорошем согласии измеренного закона дисперсии квазичастиц графена в магнитном поле с теоретическими предсказаниями. Заодно авторами было подтверждено утверждение о том, что энергия квазичастиц, находящихся на нулевом уровне Ландау, равна нулю независимо от приложенного магнитного поля.

Источник: David L. Miller, Kevin D. Kubista, Gregory M. Rutter, Ming Ruan, Walt A. de Heer, Phillip N. First, Joseph A. Stroscio. Observing the Quantization of Zero Mass Carriers in Graphene // Science. 2009. V. 324. P. 924–927.

См. также:
Graphene Yields Secrets to Its Extraordinary Properties — пресс-релиз Национального института стандартов и технологий.

Юрий Ерин