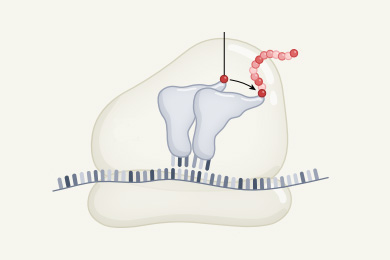
Решена давняя загадка в каталитической химии

Поверхности металлов способны расщеплять даже такие крепко связанные молекулы, как N₂. Этот процесс активно используется в химической промышленности, однако детального его понимания до сих пор нет (изображение с сайта rulgla.leidenuniv.nl)

Численное моделирование дало исчерпывающий ответ на одну из загадок каталитической химии: почему молекулам так важно, на какую именно сторону кристалла садиться. Механизмы хемосорбции теперь нуждаются в пересмотре.

Физические явления и химические реакции на атомарно гладкой поверхности кристаллов очень непохожи на те же процессы «в объеме». Например, на поверхности твердого тела могут идти процессы плавления или окисления, даже если толща материала не собирается ни плавиться, ни окисляться.

На поверхности кристаллов могут также протекать химические реакции, которые сами по себе казались бы невероятными — именно поэтому пористые пластинки некоторых металлов используют в качестве катализаторов. Даже молекула азота N₂, в которой атомы связаны друг с другом тройной ковалентной связью — одной их самых сильных в природе, — свободно диссоциирует (распадается на отдельные атомы) на поверхностях некоторых металлов, например железа. Кстати, именно этот процесс лежит в основе промышленного производства аммиака и связанного азота вообще.

Почему поверхности могут обладать каталитическими способностями, конечно, не является загадкой. Атомы и молекулы, даже разного типа, как правило, притягиваются друг к другу, и потому молекулам газа выгодно садиться на поверхность: так уменьшается суммарная энергия системы. Сев на поверхность, молекула (в данном случае N₂) попадает под действие сил тех атомов, из которых эта поверхность сложена. Металлические поверхности как бы оттягивают на себя электронные облака, связывающие два атома азота, связь ослабляется, и атомы металла разрывают «ослабевшую» молекулу.

Загадкой является другое. Уже десятки лет ученым не дает покоя вопрос: почему для диссоциации молекулы азота столь важно, на какую именно сторону, на какой именно скол кристалла она садится? Например, еще в 1980-е годы было установлено, что если взять два одинаковых кристалла вольфрама и расколоть первый вдоль главных атомных плоскостей — на языке кристаллографии, в направлении (100), — а второй расколоть под углом, в направлении (110), то каталитическая способность первого кристалла будет в сотни раз выше, чем второго. В чём причина этого эффекта — до сих пор не было известно.

Конец этой загадке положила недавняя работа испанских и аргентинских физиков. В своей статье M. Alducin et al., Physical Review Letters, 97, 056102 (31 July 2006) они описывают результаты ресурсоемкого численного моделирования тех процессов, которые происходят с молекулой азота при сближении с вольфрамовой поверхностью, и сравнивают их с опытными данными.

Подход исследователей можно назвать безыскусным, но для данной задачи он оказался самым эффективным. Последовательно перебирая несколько тысяч вариантов, авторы изучили, как меняется энергия взаимодействия молекулы с поверхностью в зависимости от шести переменных: трех координат центра молекулы, двух координат, задающих ее ориентацию в пространстве, и расстояния между атомами в молекуле. Выяснилось, что эта энергия обладает очень неровным ландшафтом. В определенных участках пространства, например непосредственно над атомами вольфрама, потенциальная энергия мала — и поэтому в эту «долину» потенциальной энергии будет втягиваться пролетающая мимо молекула. В других областях пространства вблизи поверхности есть области отталкивания, своего рода «холмы» потенциальной энергии, сквозь которые молекулы газа при обычных температурах пролететь не способны.

Оказалось, что два типа вольфрамовых поверхностей отличаются расположением холмов и долин потенциальной энергии вдали от поверхности, и именно поэтому так сильно разнятся их каталитические способности. Для поверхности (110) «первый ряд препятствий», которые подлетающая молекула встречает на расстоянии около 3 ангстрем от поверхности, расположен столь хитрым образом, что сразу попасть «в долину» можно лишь при вертикальном падении на поверхность. Если же молекула подлетает под заметным углом к вертикали, то она отражается от «предгорий» потенциальной энергии, так и не достигнув поверхности. А раз нет контакта с поверхностью, то не происходит и диссоциация. Именно поэтому каталитическая способность поверхности (110) столь низка.

Авторы, кстати, обращают внимание на то, что «догма каталитической химии» — если реакция затруднена, то значит приходится преодолевать потенциальный барьер — в этом случае дает осечку. Те молекулы, которые всё же достигают поверхности, пробираются «долинами» и вовсе не преодолевают никакого потенциального барьера. Реакция затруднена просто потому, что трудно найти такие лазейки к поверхности.

В противоположность этому, те же самые предгорья потенциальной энергии для поверхности (100) расположены в пространстве посвободнее. В результате подлетающая с любого направления молекула сразу же легко попадает в долину и уже по ней доходит до поверхности, где атомы вольфрама и расщепляют ее.

Итак, разница между каталитическими способностями двух поверхностей, как выясняется, проистекает не из разных «реакционных сил» непосредственно самих поверхностей, как подозревалось ранее, а из профилей потенциальной энергии на довольно большом расстоянии от нее (всё-таки 3 ангстрема — это целых два атомных слоя кристаллической решетки вольфрама).

Авторы завершают статью сильным заявлением о том, что их работа предлагает ни много ни мало альтернативную общепринятой точку зрения на то, как протекают химические реакции на поверхности. Не исключено, что подобные «геометрические» эффекты имеют место и для других реакций и что обнаруженное явление может вскоре привести к оптимизации промышленных химических процессов.

Игорь Иванов