Куб и окружность Эйлера
Егор Бакаев
«Квантик» №12, 2025
Куб можно схематично нарисовать на плоскости (рис. 1).

На этом рисунке 12 рёбер куба изображены как 12 равных отрезков, пусть их длины равны 1. Тогда каждая из 6 квадратных граней куба выглядит как четырёхугольник, все стороны которого равны, то есть как ромб. Мы будем рассматривать эту картинку и как изображение трёхмерного куба, и как чертёж на плоскости, и свяжем тем самым некоторые факты про куб с некоторыми фактами геометрии треугольника.
Диагонали куба
Куб симметричен относительно своего центра. Отсюда понятно, что четыре диагонали куба, соединяющие противоположные вершины, пересекаются в одной точке — центре куба. При этом каждая диагональ куба делится центром куба пополам.
Теперь рассмотрим эту картинку как обычный чертёж на плоскости. Опять же соединим противоположные вершины. Получим аналогичный факт (рис. 2) — отрезки AE, BF, CD и OH пересекаются в одной точке и делятся этой точкой пополам.
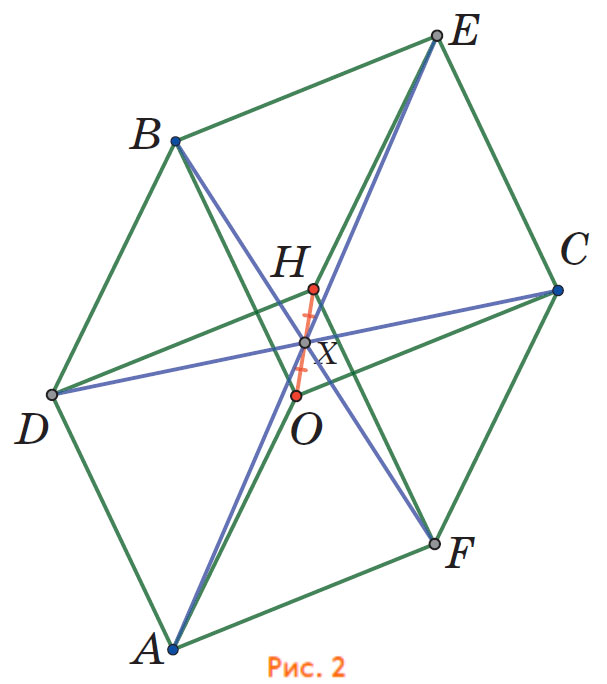
Доказать это можно так. Четырёхугольники BECO и OCFA — ромбы, поэтому отрезки BE, OC и AF параллельны друг другу, а также BE = AF. Следовательно, BEFA — параллелограмм, так как две его стороны равны и параллельны. Значит, его диагонали BF и AE делят друг друга пополам. А это как раз два из четырёх отрезков, которые нас интересуют. Аналогично рассматривая другие параллелограммы (найдите их!), для которых наши отрезки являются диагоналями, получим, что они все делят друг друга пополам, то есть проходят через одну точку. Обозначим эту точку X, она нам ещё встретится позже.
Ортоцентр
Продолжим рассматривать нашу картинку как плоскую. Обратим внимание на треугольник ABC. Где находится центр окружности, проходящей через точки A, B и C (то есть описанной окружности треугольника ABC)? Это как раз другая «вершина кубика» — точка O, потому что OA = OB = OC. Интересно, что ещё одна «вершина кубика» является замечательной точкой треугольника ABC. А именно, H — его точка пересечения высот (ортоцентр)!
Докажем это. Для этого покажем, что прямые AB и CH перпендикулярны (рис. 3). Мы уже доказывали, что BEFA — параллелограмм, значит, AB и FE параллельны. Диагонали ромба ECFH перпендикулярны, поэтому перпендикулярны AB и CH. Аналогично доказывается, что перпендикулярны BC и AH, а также CA и BH. Значит, H — ортоцентр треугольника ABC.
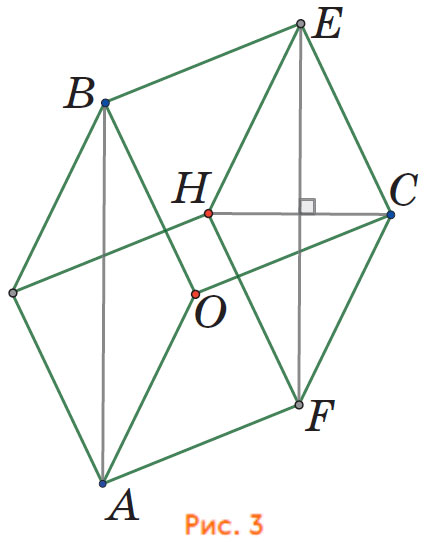
Сфера, вписанная в куб
Рассмотрим теперь центры всех шести граней куба (рис. 4). Пусть длина ребра куба равна a. Тогда все центры граней куба удалены от центра куба на одно и то же расстояние, равное a/2. Это совершенно естественное для куба свойство, ведь все его грани «устроены одинаково» относительно центра. Если соединить центры противоположных граней, получится три отрезка, параллельных рёбрам куба, длины a, проходящие через центр куба. Так как шесть точек равноудалены от центра куба, то они лежат на одной сфере с центром в этой точке — это сфера, вписанная в куб. А три отрезка длины a — диаметры этой сферы.

Центры ромбов
Во что превратится этот факт, если вместо трёхмерного куба рассмотреть изображение куба на плоскости, о котором шла речь выше? Отметим центры всех шести ромбов (со стороной 1). Докажем, что они лежат на одной окружности!
Как и раньше, соединим центры двух противоположных ромбов. Покажем, что у всех трёх таких отрезков одинаковая длина и что у них общая середина. Рассмотрим один из таких отрезков (рис. 5).

Пусть центр ромба ADBO — точка C0, а центр ромба FHEC — точка C1. (Почему выбраны такие названия точек, должно стать понятнее позже.) Нас интересует отрезок C0C1. Заметим, что ABEF — параллелограмм, и точки C0 и C1 — середины его сторон. Поэтому отрезок C0C1 равен и параллелен стороне AF параллелограмма, длина которой равна 1. Отсюда также следует, что середина отрезка C0C1 совпадает с центром параллелограмма, то есть с точкой X. Значит, все три отрезка, соединяющие центры ромбов, имеют длину 1, и их середины совпадают с точкой X. Поэтому концы этих отрезков лежат на одной окружности радиуса 1/2 (рис. 6)!
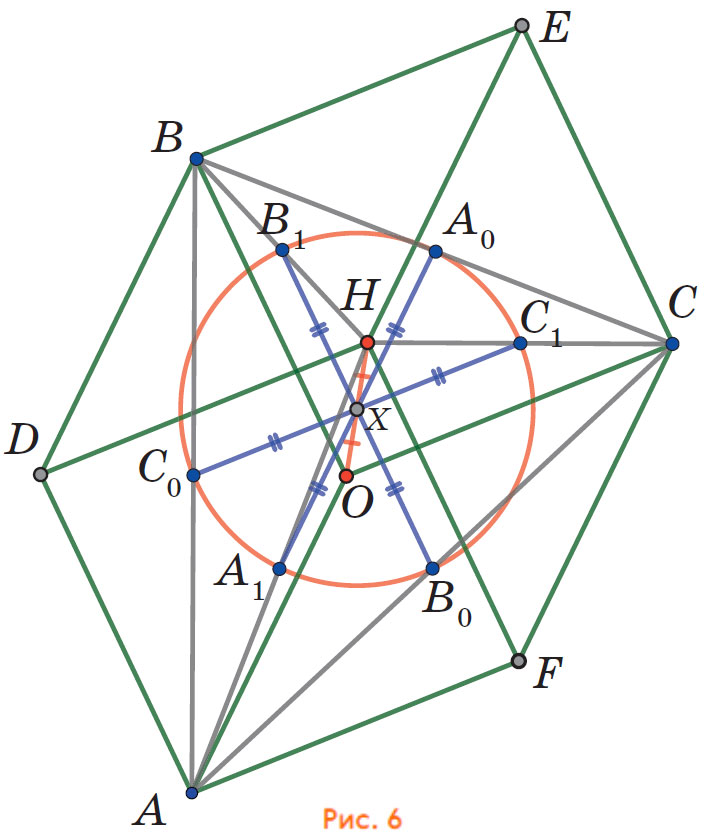
Окружность Эйлера
Обозначим концы двух других отрезков A0A1 и B0B1, как на рисунке 6. Посмотрим, какие роли выполняют шесть центров ромбов в треугольнике ABC. Точки A0, B0, C0 — это середины сторон треугольника ABC, а точки A1, B1, C1 — это середины отрезков AH, BH, CH соответственно. Таким образом, эта окружность — это знаменитая окружность Эйлера (окружность девяти точек) для треугольника ABC! В любом треугольнике на одной окружности лежат девять точек: помимо шести упомянутых, ещё на этой окружности лежат основания высот треугольника (рис. 7). Про шесть точек мы это уже доказали, осталось доказать, что на той же окружности лежат основания высот: пусть C2 — основание высоты треугольника ABC, опущенной из вершины C. Тогда угол C1C2C0 — прямой, а поэтому точка C2 лежит на окружности с диаметром C0C1, а это как раз диаметр окружности Эйлера. Аналогично, на этой окружности лежат основания и других высот.

Прямая Эйлера
Кстати, мы доказали ещё один факт, про другой знаменитый объект геометрии треугольника: центр окружности Эйлера находится в точке X и мы уже доказали, что это середина отрезка OH — одной из «диагоналей куба». Прямую, содержащую точки O, H, X, называют прямой Эйлера (помимо этих трёх точек на ней лежит ещё и точка пересечения медиан треугольника).
Задачи для самостоятельного решения
1. Докажите, что расстояние от точки O до стороны AB в два раза меньше CH.
2. В начале статьи мы сразу взяли чертёж с шестью ромбами. Но чтобы все наши утверждения считать доказанными для произвольного треугольника ABC, надо показать, что эта конструкция с шестью ромбами строится по заданному треугольнику ABC. Рассмотрите случаи:
1) ABC остроугольный, и тогда точка O лежит внутри треугольника;
2) ABC тупоугольный, и тогда точка O лежит снаружи треугольника;
3) ABC прямоугольный, и тогда точка O лежит на одной из сторон треугольника. В этом случае на рисунке будет не 6 ромбов, а 2 — но попробуйте всё же найти на нём 9 точек окружности Эйлера, и подумайте, во что вырождаются другие утверждения, о которых мы говорили.



























Художник Алексей Вайнер