Превращения графов
Валерия Сирота
«Квантик» №10, 2024
Вы, конечно, знаете, что такое графы — столько раз это в «Квантике»1 обсуждалось, как же не знать? Если говорить просто, это точки, соединённые линиями. Точки называются вершинами графа, линии (не обязательно прямые) — его рёбрами.
Вершины графа могут быть просто-так-сами-по-себе-точки, а могут что-нибудь означать. Например, в родословных вершины графа — люди, а рёбра графа соединяют мужей с жёнами и родителей с их детьми2. Или вершины графа могут обозначать ребят в классе, а линии — кто с кем дружит. Нарисовать такой граф можно по-разному — важно лишь, какие вершины с какими соединены.
Поэтому граф — это удобный способ изобразить что-то, когда нам не нужны никакие «внутренние» свойства рассматриваемых объектов, а важны только их связи с другими объектами. Например, если нам неважно, какой формы и размера страны, а важно, с кем они граничат, — можно обозначать страны точками, а те из них, которые имеют общую сухопутную границу, соединять линией.
Тогда граф стран острова Ирландия выглядит так:
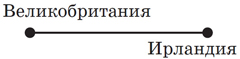
Задача 1. Нарисуйте граф стран Южной Америки (а можно сразу и Южной, и Северной) без островов (карту можно найти в интернете). Если вам понравилось, можно ещё и графы стран Азии или Европы нарисовать — это немного сложнее.
Бывает, что граф можно уложить на плоскости без самопересечений: ровненько, так что ни одна линия (ребро графа) другую не пересекает (например, это получится в задаче 1). А бывает, что это сделать нельзя; тогда приходится в месте пересечения рёбер рисовать что-то такое:  . Или такое:
. Или такое:  .
.
Ну всё, разминка кончилась, теперь держитесь! Главное — не запутаться: в одной и той же задаче у нас может встретиться многогранник со своими вершинами и рёбрами, и граф — со своими. Для ясности вместо «вершины графа» будем по старинке говорить «точки», а вместо «рёбра графа» — «линии».
Возьмём обычный кубик (рис. 1). Глядя на него, можно построить целых три графа — смотря что мы договоримся обозначать точками и линиями.
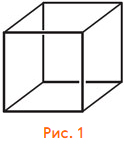
Задача 2. Нарисуйте графы а) вершин; б) граней; в) рёбер кубика.
То есть на первом графе точками будут вершины куба, а линиями нужно соединить те из них, которые на кубе соединены ребром. На втором графе точки — уже грани нашего кубика, а линии соединяют те грани, которые граничат друг с другом, то есть у которых есть общее ребро. На третьем графе точками будут рёбра куба, и те из них, что имеют общую точку (сходятся в одной вершине), нужно соединить линиями. Условие этой задачи можно записать в такую таблицу:
| Задание | Вершины графа (точки) | Соединены линией, если: |
| а) | Вершины куба | На одном ребре куба |
| б) | Грани куба | Имеют общее ребро куба |
| в) | Рёбра куба | Имеют общую вершину куба |
Проверьте, правильное ли количество «точек» получилось на ваших графах? Одинаковое ли (и правильное ли) количество линий выходит из каждой вершины («точки») графа? И не спешите сразу смотреть в ответы: сначала решите ещё хотя бы пару задачек.
Подсказка-«спойлер»: сам рисунок прозрачного кубика (такого, что на рисунке видны и передние, и задние рёбра — рис. 1) — это уже ответ на первый вопрос задачи! Каждая вершина обозначает сама себя. Только этот граф — с пересечениями. А точки и соединяющие их линии на графе можно ведь двигать: линии при этом могут растягиваться и изгибаться, как резиновые. Главное, чтобы линии не «рвались» и по-прежнему соединяли нужные пары точек. Давайте потренируемся рисовать одни и те же графы разными способами!
Задача 3. Сможете ли вы нарисовать все эти графы так, чтобы линии не пересекались?
Задача 4. Сможете ли вы нарисовать все эти графы (с пересечениями и без них) так, чтобы у них было как можно больше осей симметрии?
Решение задач 2–4
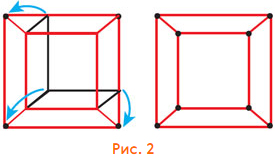
а) Подойдёт рисунок 1. Этот граф имеет ось симметрии, но у него пересекаются рёбра. Эти пересечения легко убрать, и даже повысить степень симметрии при этом (рис. 2).
б) Возьмём развёртку куба, отметим точкой середину каждой грани и соединим склеиваемые грани (рис. 3).
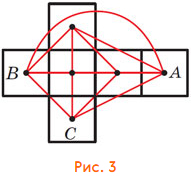
У полученного графа нет самопересечений, но он несимметричен. Чтобы сделать его и непересекающимся и симметричным, можно сместить вправо нижнюю вершину графа и немного подвинуть остальные (рис. 4). Тут 3 оси симметрии. Можно сделать и 6, но ценой появления пересечений (рис. 5).
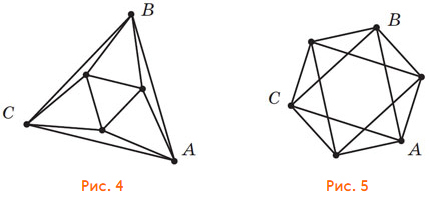
в) Это задание — посложнее. Можно, например, начать с какого-нибудь угла куба и с соединяющихся в этой вершине рёбер. Удобно пронумеровать рёбра куба, то есть вершины нашего графа, и следить, кто с кем соединяется (рис. 6).
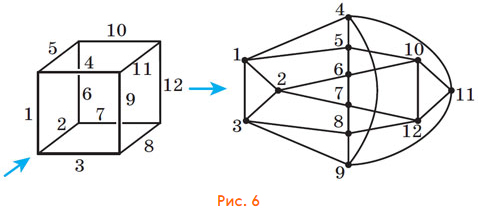
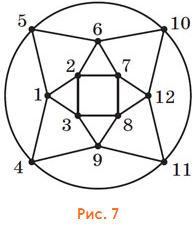
А если «посмотреть на кубик сверху», можно построить граф без самопересечений и с четырьмя осями симметрии (рис. 7).
А ведь графы могут быть не только на плоскости, но и в пространстве! Или на сфере, например, можно их рисовать — вот хоть на поверхности мячика. Или даже на поверхности бублика. И многие графы, которые не нарисуешь без пересечений на плоскости, на бублике прекрасно помещаются.
Задача 5. Как можно более симметрично расположить наши три графа не на плоскости, а в пространстве (например, если бы вы делали их из пластилина и проволочек)? Какие симметричные пространственные фигуры (многогранники) у вас получились бы?
Подсказка
Можно прямо на изначальном кубике поставить точки в середину того, что вы хотите ими обозначить — в середину каждой грани для графа граней, в середину каждого ребра для графа рёбер... и в саму вершину для графа вершин! У вас уже получится симметричная пространственная конструкция. Дальше надо только правильно соединить эти точки отрезками.
Теперь у вас должно было получиться три симметричных пространственных многогранника. Давайте повторим ту же процедуру «делания графа» ещё раз — только уже не из кубика, а из многогранника, который мы получили из этого кубика путём построения графа.
Задача 6. Какой многогранник возникнет, если взять первый из наших трёх многогранников и сделать граф его вершин? А что получится из второго многогранника (графа граней), если сделать (пространственный и симметричный) граф его граней? И, наконец, что получится из третьего графа, если сделать граф его рёбер? В последней задачке договоримся соединять линией лишь те рёбра многогранника, которые не только соединяются в одной точке, но ещё и принадлежат одной и той же грани.
Решение задач 5–6
Пространственный граф вершин куба — сам куб. Сколько эту процедуру ни повторяй, будет получаться одно и то же.
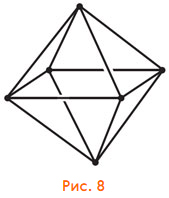
Граф граней — октаэдр (рис. 8). Его легко получить, просто нарисовав точки — вершины графа — на серединах граней куба. А что будет, если опять взять середины граней? — Снова куб (рис. 9).
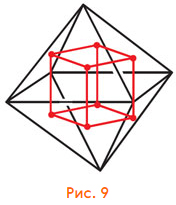
Пространственный граф рёбер тоже легко построить — просто отметить точками середины рёбер и соединить нужные (рис. 10). На плоскости картинка получается не очень-то симметричной, зато в пространстве — симметричнее не сделаешь. Это многогранник из равносторонних треугольников и квадратов: «куб с отрезанными углами», называется кубооктаэдр.
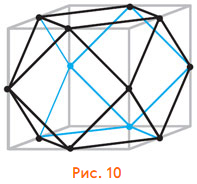
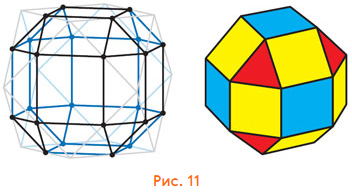
У него 12 вершин и 12·4/2 = 24 ребра (потому что из каждой вершины выходит 4 ребра). Как будет выглядеть граф его рёбер? Нарисовать его «поверх» предыдущего рисунка сложновато... но можно представить, как он выглядит, или нарисовать развёртку. У него 24 вершины — столько, сколько рёбер у кубооктаэдра. Из каждой вершины выходит 4 ребра (потому что каждое ребро кубооктаэдра имеет 4 смежных по стороне ребра). Всего 24·4/2 = 48 рёбер. Те грани, которые у кубооктаэдра были квадратами, превратятся в квадраты, повёрнутые на 45°; грани, которые были треугольниками, снова дадут треугольники. Но появятся ещё новые квадраты: теперь вокруг каждого треугольника уже не 3, а 6 квадратов. Мы, конечно, не можем быть заранее уверены, что получится многогранник именно с квадратами, а не какими-то четырёхугольниками. Но такой многогранник существует. Это ромбокубооктаэдр (рис. 11).
Ну и, наконец, на «заминку» –
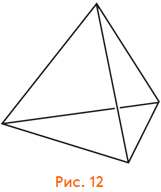
Задача 7. Проделайте все те же упражнения с тетраэдром (рис. 12)!
Решение задачи 7
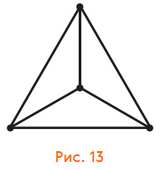
Граф граней у тетраэдра — это снова тетраэдр. На плоскости его удобнее всего нарисовать, посмотрев на тетраэдр сверху (рис. 13).
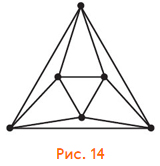
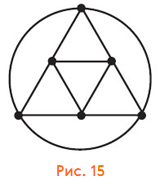
Граф рёбер выглядит так, как на рисунке 14 или 15 (что то же самое). А в пространстве это — тот же самый октаэдр, что нам уже встречался в задаче 5: 6 вершин, каждая соединена с четырьмя другими. (Какие пары рёбер соответствуют на графе противоположным точкам?)
Ну а «граф рёбер графа рёбер» это — о чудо! — снова кубооктаэдр, как в задаче 5.
1 См. статьи в «Квантике»: К. Пахомова «Спичечные графы» (№8, 2015), К. Кохась «Портрет его сиятельства» (№3, 2017), «Домики и колодцы на чайной кружке» (№8, 2020); В. Уфнаровский «Их сиятельство граф» (№8, 2021).
2 На рёбрах ещё иногда ставят стрелки — например, чтобы показать в родословной, кто родитель, а кто ребёнок и т. п.






















Художник Алексей Вайнер