Равные площади в правильных многоугольниках
Материал подготовил Григорий Мерзон
«Квантик» №10, 2024
Соединим точку внутри квадрата с вершинами квадрата (рис. 1). Какая из площадей больше — светлая или тёмная?
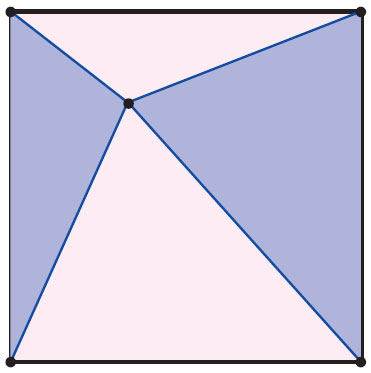
Рис. 1
Оказывается, какую бы точку мы ни взяли, суммарная площадь двух противоположных частей всегда одна и та же и равна половине площади квадрата. Это совсем не трудно понять, если провести через нашу точку вертикальную и горизонтальную прямые (рис. 2): они разбивают квадрат на части, в каждой из которых обоих цветов поровну.

Рис. 2
Можно рассуждать и по-другому. Площадь треугольника равна половине произведения его основания на высоту. Основание каждого из четырёх треугольников на рисунке является стороной квадрата. А сумма высот треугольников одного цвета всегда одна и та же (они как раз складываются в «высоту квадрата», рис. 3).

Рис. 3
Замечательно, что это утверждение можно обобщить — и даже в двух направлениях.
Во-первых, можно вместо квадрата рассматривать другие правильные многоугольники (у которых равны все углы и все стороны). Например, для шестиугольника получается даже два утверждения (рис. 4): можно покрасить части в шахматном порядке, а можно последовательно в три цвета — и в обоих вариантах общая площадь для каждого из цветов одна и та же, какую бы точку внутри многоугольника мы ни брали. Попробуйте, кстати, это доказать! Возможно, вам пригодится утверждение из заметки «Теорема Вивиани» в «Квантике» №9 за 2022 год.
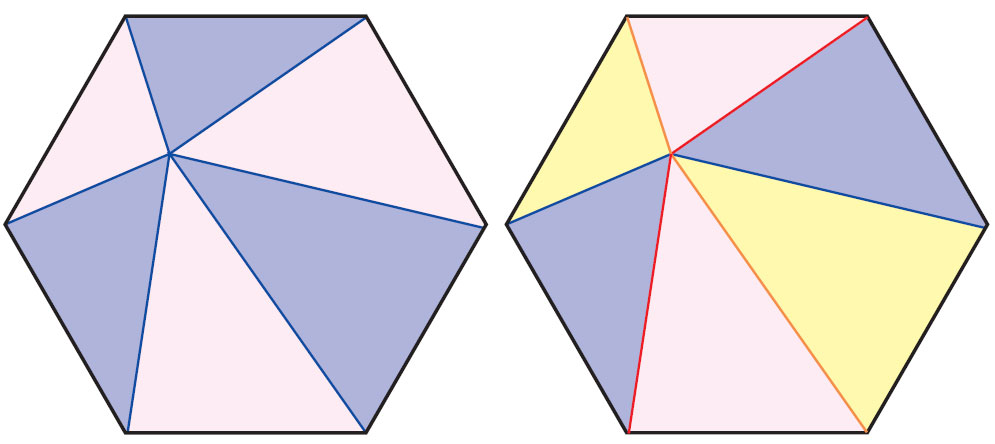
Рис. 4
Во-вторых, можно внутри правильного N-угольника выбирать не точку, а другой правильный N-угольник, и соединять соответствующие вершины. Попробуйте доказать и это утверждение. Советуем начать с квадрата (рис. 5). Если не будет получаться, подсказку можно найти в замечательной книге «Задачи на вырост» В. В. Произволова.
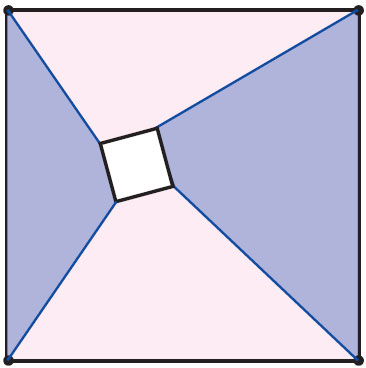
Рис. 5

















Художник Лиза Гожая