Неквадратный Пифагор

Материал подготовил Григорий Мерзон
«Квантик» №8, 2024

Теорема Пифагора гласит: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Можно построить на каждом из катетов по квадрату, разрезать их на части и сложить квадрат, построенный на гипотенузе¹.

Но на сторонах не обязательно строить именно квадраты! Площадь любой фигуры при растяжении в k раз увеличивается в k² раз. Поэтому можно вместо квадратов строить на сторонах правильные треугольники, или шестиугольники, или ещё что-нибудь.

На картинках ниже демонстрируется теорема Пифагора при помощи разрезания пятиугольников.

А вот самая, наверное, экономная из подобных картинок. Она основана на том, что высота из вершины прямого угла делит любой прямоугольный треугольник на два треугольника такой же формы, как исходный².

То есть исходный треугольник с гипотенузой c разбит на два треугольника такой же формы, но других размеров: с гипотенузой a и с гипотенузой b. Так как площадь целого есть сумма частей, получаем, что с² = a² + b².

На последней картинке на сторонах треугольника построили как на диаметрах полукруги. Полукруг, построенный на гипотенузе, наложился на полукруги, построенные на катетах. Выкинем их общую часть. От большого полукруга остаётся наш треугольник, а от двух меньших кругов — луночки сложной формы. Равенство площадей при этом сохранится (из обеих частей равенства мы вычли одно и то же: площадь пересечения).

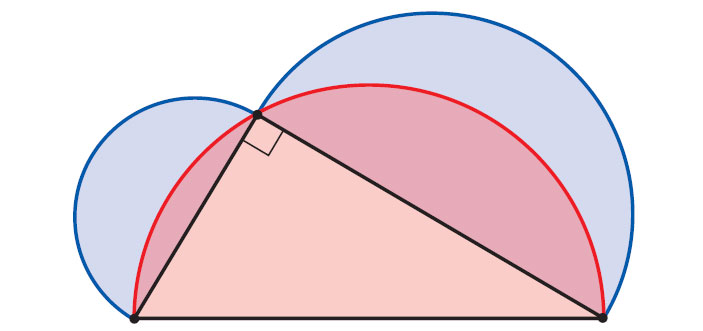
Значит, суммарная площадь двух луночек³ (их называют гиппократовыми) равна площади треугольника. Это довольно удивительно, особенно если припомнить, что в формулу для площади круга входит странное число π.

Художник Алексей Вайнер

---

¹ Резать можно многими разными способами. Можно поиграть в некоторые из них на сайте Математических этюдов или сделать свою модель самому!

² Чтобы в этом убедиться, подумайте про углы этих треугольников.

³ Кое-что ещё про площадь луночек можно узнать из статьи В. Кириченко и В. Тиморина «Квадратура луночки» в «Квантиках» №№2–3 за 2022 год.