Путь наименьшего сопротивления

Александр Бердников
«Квантик» №5, 2024

Часто задачки-парадоксы на физическое воображение предлагают разобраться, как будет двигаться какая-то машинерия, если на неё так-то надавить. Вот несколько примеров:

1. Куда покатится катушка, если за нитку потянуть, как на фотографиях?

2. А если подтолкнуть катушку за прикреплённую вот так зубочистку?

3. Куда поедет велосипед, если потянуть за педаль (с помощью красного шнура)?

4. Может ли устройство, изображённое ниже, двигаться на ветряной тяге навстречу ветру? А быстрее ветра? В устройстве колёса связаны с пропеллером так, что за каждый оборот колёс пропеллер делает фиксированное число оборотов; никаких внутренних источников энергии нет.

Такие задачи могут сбивать с толку при подходе «в лоб». Если пытаться последовательно представлять, как приложенное усилие распространяется по телу, как в ответ земля начинает на него давить и так далее, то легко увязнуть и запутаться. И даже пятёрки по физике не гарантируют, что вы легко возьмёте эти задачи грубой силой вычислений и формул, не поддавшись обманчивой интуиции. Например, ошибочное решение задачи 3 можно встретить в научно-популярной книге выдающегося математика В. И. Арнольда «Математическое понимание природы», а двое физиков, споря о задаче 4, дошли аж до пари на $10 000 (см. видео по запросу Veritasium, faster than wind videos? в интернете).

Но стоит подойти к этим головоломкам с другого конца — и они вмиг упрощаются. Спросим, не «что наш толкающий палец может сделать с машиной», а «что машина может сделать с пальцем». Если она была в равновесии («сама по себе никуда ехать не хотела»), то ничего она не может сделать, кроме как поддаться. Если бы у неё «были силы» перебороть давление пальца — толкая его, а не поддаваясь, — то без его сопротивления она бы и подавно туда сама поехала. Это главное соображение:

Если надавить на тело в равновесии, оно в точке давления сдвинется попутно давлению.

Это и так понятно в простых ситуациях: куда шар на столе толкнули, туда он и покатился. Но теперь можно легко решать задачи и посложнее. Можно не разбираться со сложной системой сил, — просто катаем машину туда-сюда и смотрим, как её части двигаются, выбираем то движение, при котором она поддаётся давлению, а не перебарывает его. Например, если катушка из задачи 2 катится вправо, то и верх зубочистки идёт вправо. Но другие точки катушки и зубочистки будут двигаться по-другому. Например, у самого стола они ни влево, ни вправо не будут двигаться, если катушка не скользит по неподвижному столу. Но тогда под столом зубочистка сдвинется в противоположную сторону, влево (см. рисунок). Значит, если надавить на зубочистку под столом, катушка покатится навстречу! Ведь не важно, как она движется в целом; главное, чтобы в точке, на которую давим, она двигалась от нас, а остальное — уж как по лучится.

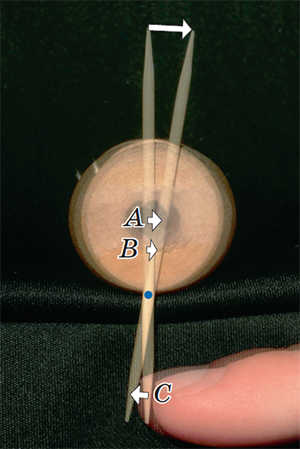
В задаче 1 верёвка прилагает силу к катушке в другой точке, над столом; можно считать, что эта верёвка привязана к зубочистке в точке B. Теперь поддаваться должна эта точка B, а раз она и центр катушки (точка А) всегда движутся в одном на правлении, то и сама катушка покатится в направлении силы (наматывая на себя верёвку, хоть мы её и пытались вытянуть). Вы можете сами так же проверить, что в случае, когда мы тянем нить вверх, катушка, наоборот, будет разматываться.

Велосипед в задаче 3 мало отличается от катушки, и шаги в решении те же самые. Куда движется точка приложения силы (педаль), когда мы катаем велосипед взад-вперёд: по ходу движения велосипеда или против? Тут можно было бы сделать расчёты по картинке, но можно обойтись и здравым смыслом. Зачем вообще нужны педали велосипеду, если мы могли бы ногами прямо от земли отталкиваться? Это приходилось бы делать с той скоростью, с которой мы едем, а педали позволяют (в том числе) крутить их гораздо медленней, но с тем же эффектом. Поэтому они движутся по ходу движения велосипеда (иначе для ездока они бы шли назад даже быстрее, чем земля). Значит, куда мы их потянем, туда он и поедет. Тут уместно задаться следующим вопросом.

Рис. 1

В случае с машинкой с пропеллером мы будем считать, что давление ветра на всё, кроме пропеллера, можно сделать пренебрежимо малым (делая конструкцию тонкой) и что лопасти сами не испытывают трения о воздух, он только давит на их поверхность, как на парус. Можно для наглядности представить (рис. 1), что они — бесконечно тонкие, часть этакой винтовой поверхности, вдоль которой они могут скользить, вращаясь вокруг оси и двигаясь вперёд. Для удобства положим, что эта поверхность — и винт, вдоль неё скользящий, — делают один оборот за метр.

Теперь мы готовы ответить на ключевой вопрос, который опять такой: при каких движениях поверхность лопастей поддаётся напору ветра, а при каких идёт навстречу? Покатаем машинку. Если винт будет при этом совершать один оборот за каждый метр, проезжаемый машиной, то сама винтовая поверхность с лопастями никуда не сдвинется (рис. 2а), винт лишь проскользит внутри неё, так ветру не поддашься. Если же винт при движении машины совсем не вращается, то поверхность лопастей сдвигается вместе с ним и вместе с машиной как парус (рис. 2б). Настраивая связь между колёсами и винтом, можно создать промежуточную ситуацию, чтобы винт делал меньше одного оборота за метр. Тогда поверхность лопастей сдвигается по ходу машины, но меньше, чем сама машина (рис. 2в), и чтобы поддаться ветру вперёд, машинка поедет вперёд. И будет поддаваться и разгоняться до тех пор, пока парус не поддастся полностью, то есть его поверхность не станет двигаться вместе с ветром. И коли движение машины (серая стрелка на рисунке) у нас больше, чем сопутствующее ей движение поверхности паруса (чёрная стрелка), который движется со скоростью ветра, машина будет двигаться в этом случае быстрее ветра, который её двигает.

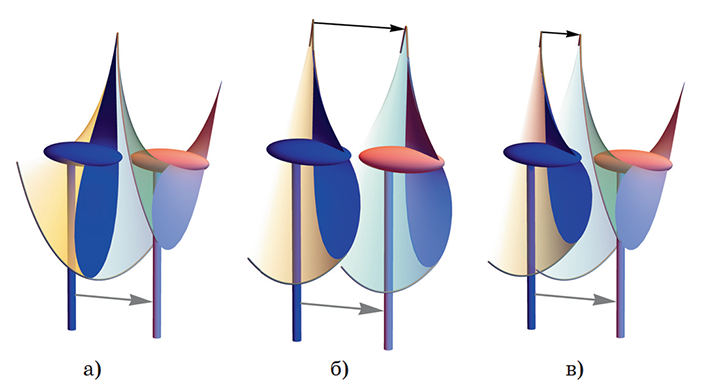
Рис. 2

Эта ситуация — лишь завуалированная катушка из задачи 2, которую толкают в точке B. В случае катушки неудивительно, что сама катушка (точка A) смещается быстрее, чем то, что её толкает (в точке B). Можно ещё сблизить эти примеры, если представить, что у катушки в точке B парус, и толкается он ветром. Возникнет небольшая проблема: по мере разгона катушка повернётся, и парус окажется уже в другом положении. Но это можно исправить, установив кучу свёрнутых парусов, которые у точки B разворачиваются, а уйдя — сворачиваются обратно, так что ветер всегда давит около точки B.

С другой стороны, если связь между колёсами и пропеллером настроить так, что при движении машины поверхность пропеллера движется в противоположную сторону, мы получим будто бы катушку, которую толкаем в точке C. Пропеллер поддаётся ветру, движется в его сторону, а машина тогда — навстречу.

Вот так легко можно понимать некоторые механические загадки, ища не «что произойдёт при попытке так-то надавить», а «что должно было случиться, если попытка надавить удалась». Но надо учитывать пару деталей. Этот трюк даёт простой ответ в случаях, когда у системы есть только один способ подвигаться вперёд-назад — тогда если движение «назад» идёт наперекор давлению, у нас остаётся единственное «вперёд». Но если система может сдвинуться из исходного положения многими разными способами, многие из них могут поддаваться давлению, и остаётся неопределённость. Если я толкну край руля велосипеда вперёд, то и руль повернётся, и велосипед вперёд поедет, но непонятно, будет ли какое-то из этих движений доминировать и насколько. И иногда эти «другие движения» прячутся от глаз, как в следующем примере.

Художник Алексей Вайнер