Справедливый делёж, последовательность Туэ — Морса и снежинка Коха

Валентина Кириченко, Владлен Тиморин
«Квантик»№12, 2023

Как разлить чай из чайника по двум чашкам, чтобы в итоге получить две порции чая примерно одной и той же крепости? Обычно в заварочном чайнике (если не перемешивать содержимое) более крепкий чай образуется на дне, а более водянистый — на поверхности. Если налить доверху сначала первую чашку, а потом — вторую, в первой чашке чай будет не таким крепким, как во второй. Это не очень-то справедливо, если вы хотите угостить чаем друга, а тот любит такой же крепкий чай, как и вы. Мы расскажем о более справедливом способе и его далеко идущих обобщениях.

Нужно сначала налить чай в первую чашку, но не доверху, а до середины. Затем целиком заполнить вторую чашку. Наконец вернуться к первой чашке и заполнить её. Схематически церемонию справедливого розлива чая можно изобразить такой последовательностью:

AББA

Буквы А и Б указывают на то, в какую именно чашку нужно налить полчашки чая. Можно договориться, что если А, то наливаем другу, если Б — себе. После этой нехитрой процедуры чай в обеих чашках будет примерно одной крепости, в чём легко убедиться по его цвету.

Педанты могут попытаться улучшить процедуру АББА. Для чая это уже не столь актуально, но в футбольных соревнованиях может пригодиться. Если две команды сыграли вничью, то для определения победителя обычно используется серия из десяти пенальти (пять раундов по два пенальти), после чего побеждает команда, набравшая больше очков по пенальти. Если же и здесь получилась ничья, то раунды добавляются по одному до первого раунда с результатом 0:1 или 1:0. Именно так выиграла команда ФРГ в знаменитом матче с командой Франции в полуфинале чемпионата мира по футболу в 1982 году. В шестом раунде французский игрок не смог забить пенальти (он бил первым по очереди), а немецкий игрок смог (он бил вторым). При таком способе определения победителя вторая команда часто испытывает большее психологическое давление: если первая команда забивает пенальти в очередном раунде, то второй команде надо непременно сравнять счёт, чтобы не проиграть сразу же. Поэтому футбольные ассоциации серьёзно рассматривают возможность заменить последовательность АБАБАБ... (в каждом раунде первой бьёт команда А) на более справедливую последовательность. Например, на такую:

AББAБААБ

Это начальный фрагмент длины 8 последовательности Туэ — Морса, о которой мы теперь расскажем поподробнее. Она формируется из двух букв (или из цифр 0 и 1) по следующему принципу. Первая буква A. Начальный фрагмент длины 2 получается приписыванием другой буквы (не А), в нашем варианте это Б (хотя часто используют латинское В). Начальный фрагмент длины 4 получается приписыванием «зеркального варианта» фрагмента длины 2: каждая А меняется на Б, а каждая Б — на А. Получается уже знакомая нам последовательность для справедливого розлива чая: АББА. Начальный фрагмент длины 8 получается приписыванием зеркального варианта фрагмента длины 4. Получается справедливая последовательность пенальти. Можно пойти дальше и выписать фрагмент длины 16:

AББAБААББААБАББА

Последовательность Туэ — Морса можно продолжать таким образом сколько угодно, каждый раз длина фрагмента будет удваиваться. За 10 удвоений получится фрагмент приличной длины — 1024 буквы. В футболе такое вряд ли пригодится — самая длинная на сегодняшний день серия пенальти состояла из 54 попыток (то есть из 27 раундов). Однако даже очень длинным фрагментам последовательности Туэ — Морса можно найти красивое применение. С их помощью легко нарисовать хорошие приближения кривой Коха (см. рисунки вверху следующей страницы) — изящной самоподобной кривой (такие геометрические объекты часто называют фракталами). Доказательство мы приводить не будем, но сейчас объясним, как провести подтверждающие эксперименты.

Несколько начальных приближений к кривой Коха. Начать построение следует с ломаной, показанной слева вверху. Каждое звено этой ломаной нужно заменить уменьшенной копией той же ломаной и продолжать этот процесс до бесконечности. Кривая Коха получается в пределе

Заметим, что выше мы использовали последовательность Туэ — Морса, точнее её начальные фрагменты, как программу действий, или алгоритм. То есть как нечто вроде компьютерной программы, только не для компьютера, а для хозяина, разливающего чай по чашкам, или для судьи, определяющего очерёдность пе нальти. Эту аналогию можно развить и превратить последовательность Туэ — Морса в настоящую компьютерную программу для черепашки из языка Лого¹.

Представим себе черепашку, которая за один ход может исполнить одну из двух команд.

Первая команда — повернуть на 120° по часовой стрелке и проползти один шаг. Эту команду мы схематически изобразим символом «острый угол + стрелка».

Вторая команда — повернуть на 60° против часовой стрелки и проползти один шаг. Изобразим её символом «тупой угол + стрелка».

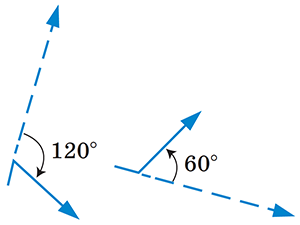
Почему символы выбраны именно так? Рядом нарисован маршрут черепашки, выполняющей первую команду (слева) и вторую (справа). Пунктиром обозначено исходное направление движения (куда черепашка ползла бы дальше, если бы не повернула). Видно, что маршруты похожи на выбранные нами символы.

Теперь проинтерпретируем последовательность Туэ — Морса как последовательность команд для черепашки. Каждая буква задаёт один ход черепашки. Первый ход особенный, поскольку тут не очень важно, как черепашка повёрнута. Для определённости договоримся, что за первый ход она проползает один шаг на восток. Эту особую команду изобразим символом «просто стрелка».

Символ «просто стрелка» встретится ровно один раз, в самом начале программы. Он соответствует первой букве A. Дальше будем двигаться вдоль последовательности Туэ — Морса и заменять каждую букву на команду по следующему правилу. Если перед текущей буквой стоит такая же буква, то приписываем к программе команду «острый угол + стрелка». Если нет, то приписываем команду«тупой угол + стрелка».

Например, начальный фрагмент длины 16 превратится в такую последовательность команд:

Если черепашка будет ползти в соответствии с заданной программой из 16 команд, то она оставит след, уже немного напоминающий кривую Коха.

Вы можете сами поработать черепашкой, для этого вам понадобятся только карандаш и бумага, расчерченная на треугольники². Можно рисовать и на обычной бумаге, если у вас хороший глазомер.

Задача 3. Изобразите путь черепашки, выполняющей программы:

а) ААА; б) АБАБАБ; в) ААББААББААББ.

Задача 4. Напишите программу, которая позволит черепашке проползти вдоль нарисованной справа снежинки (не Коха).

Выполнить программу из 64 или 256 команд с помощью карандаша и бумаги уже не так легко, хотя и существенно легче, чем забить такое же количество пенальти. Для ускорения процесса можно воспользоваться компьютером. По ссылке расположен код (на языке Python), результаты выполнения которого можно сразу увидеть в правом окне, нажав на зелёную кнопку (с изображенным на ней белым треугольником) под текстом программы. Содержательно экспериментировать с траекториями черепашки можно даже не разбираясь в основном коде, а меняя только последнюю строчку. Там сейчас написано move(thue(8),4). А смысл этой строчки состоит в следующем: move — это процедура, запускающая черепашку, thue(8) — это строчка, представляющая программу движения черепашки (в настоящий момент это начальный фрагмент последовательности Туэ — Морса длины 256, но можно вместо thue(8) вписать любую строчку, заключённую в одинарные или двойные кавычки, например, ‘AAA’ или ‘ABABAB’); наконец, 4 — это длина каждого шага черепашки (если шагов мало, то эту длину стоит увеличить). Для начала впишите вместо thue(8) какую-нибудь короткую строчку и поставьте вместо 4 какое-нибудь число побольше (скажем, 100). Например, попробуйте написать move(‘AABAB’, 100) и посмотрите, как будет двигаться черепашка. Удачных экспериментов!

Художник Мария Усеинова

¹ Старый язык программирования, изначально разработанный для обучения детей компьютерным наукам. Об очень похожем на Лого языке программирования Малыш можно прочесть в увлекательной книжке А. К. Звонкина «Малыши и математика», МЦНМО, 2022, с. 85–89.

² Треугольную сетку можно скачать или распечатать с мышематического сайта Евгении Кац.