Лёд, вода и пар
Игорь Акулич
«Квантик»№12, 2023
Студентам, изучающим теплотехнику, чтобы они лучше «прочувствовали» некоторые особенности обыкновенной воды, нередко предлагают такую задачу.
При поиске ответа на вопрос полезно взглянуть в таблицу, где приведены некоторые справочные данные (их легко найти в интернете). Вот чему равно количество тепла (в килоджоулях), необходимое, чтобы при нормальном давлении:
| − нагреть 1 кг льда от −100 °С до 0 °С | 170 |
| − растопить 1 кг льда | 330 |
| − нагреть 1 кг воды от 0 °С до 100 °С | 420 |
| − испарить 1 кг воды | 2300 |

Взглянув на эти числа, постарайтесь сначала угадать ответ с ошибкой хотя бы не более 5 градусов. А потом проверьте свою догадку, выполнив расчёт или читая дальше. Возможно, будет повод удивиться!
* * *
Въедливый читатель может спросить: а возможно ли в такой «пёстрой» смеси поддерживать постоянное нормальное давление? В самом деле, при нагревании льда объём его хоть немного, но растёт, зато при таянии он существенно снижается (почти на 10%). С водой ничуть не проще: при нагревании от 0 до 4 °С её объём опять-таки уменьшается, но после этого, наоборот, увеличивается (и чем дальше, тем сильней). А с паром вообще катастрофа: при его конденсации объём резко падает — в сотни раз. Но изменение объёма мгновенно влечёт изменение давления (как правило, в обратную сторону). Вот и попробуй поддерживать постоянное давление после смешивания всех компонентов! К счастью, есть испытанные способы добиться практически постоянного давления — например, поместить смесь в цилиндрический сосуд, верхняя часть которого ограничена подвижным поршнем. Вес поршня вкупе с наружным атмосферным давлением и создают нужное постоянное давление в сосуде (поршень «ходит» по необходимости вверх-вниз).

Впрочем, мы отвлеклись от сути задачи. Вернёмся к делу.
Возьмём 1 кг льда и будем постепенно нагревать его, пока он весь не превратится в пар. Этот процесс разобьётся на четыре этапа. Вот они:
1) нагревание льда от −100 °С до 0 °С;
2) плавление льда (превращение его в воду) — при этом температура будет постоянной и равной 0 °С, пока весь лёд не растает;
3) нагревание воды от 0 °С до 100 °С;
4) кипение воды — при этом температура будет постоянной и равной 100 °С, пока вся вода не выкипит.
Если продолжать подводить тепло дальше, пар начнёт перегреваться и температура его станет подниматься выше 100 °С, но это уже выходит за пределы нашей задачи, так что здесь притормозим.
Величины затрат тепла на все этапы были указаны как справочные в условии. Давайте теперь изобразим всё это схематично в виде диаграммы, причём в масштабе. Четыре разноцветных (и соответственно пронумерованных) столбика как раз соответствуют четырём этапам.

Что сразу бросается в глаза? Конечно, подавляющее превосходство высоты четвёртого столбика над первыми тремя. Она, очевидно, больше не только высоты каждого из трёх остальных столбиков, но и их суммы, притом в несколько раз! То есть, чтобы лишь испарить воду, требуется затратить во много раз больше тепла, нежели для нагревания льда, его плавления и последующего нагревания воды до ста градусов.
Но как это относится к нашей задаче? Самым непосредственным образом! Если такое огромное количество тепла надо затратить на испарение, то в точности такое же количество будет выделено, если сконденсировать пар, превращая его обратно в воду. А ведь у нас как раз такое явление имеет место.

В самом деле, попавший в сосуд пар начнёт постепенно конденсироваться, выделяя тепло, которое пойдёт на нагревание льда, его плавление и последующее доведение образовавшейся воды до температуры 100 °С — и этого с избытком хватит. Более того, его же хватит и на нагревание до 100 °С второй компоненты нашей смеси — воды при изначально нулевой температуре.
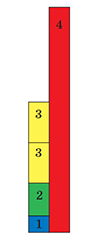
А чтобы это утверждение не выглядело голословным, изобразим всё это опять же на диаграмме, поставив друг на друга первые три столбика (что соответствует количеству тепла, потребному для доведения до 100 градусов исходного льда) и дополнительно ещё раз третий столбик (что соответствует подогреву до той же температуры исходной воды) и приложив слева к четвёртому столбику.
Что мы видим? Суммарная высота синего, зелёного и двух жёлтых столбиков составляет где-то 60% от высоты красного (точную величину можете подсчитать сами — числа возьмите из таблицы). А это как раз означает, что примерно 0,6 кг попавшего в сосуд пара сконденсируется, причём выделившегося при этом тепла будет достаточно, чтобы преобразовать остальные два компонента смеси в воду при температуре 100 °С. А оставшаяся часть пара (около 0,4 кг) так паром и останется.
Вот и ответ: температура получившейся смеси составит ровнёшенько 100 °С — и ни градусом меньше! А получившаяся смесь будет содержать 2,6 кг воды и 0,4 кг пара.
Обычно эта задача предлагается, чтобы решающий хорошенько прочувствовал, насколько велика теплота парообразования воды. Это очень важный фактор для многих технологических процессов, в частности — при работе тепловых и атомных электростанций, вырабатывающих основную часть электроэнергии в мире (ведь вода в большинстве из них — главное «рабочее тело»).
Художник Мария Усеинова
-
Теплота парообразования указывается при постоянном давлении и "учитывает" эту работу. То есть если мы в сосуд с поршнем нальём литр воды при температуре 100 градусов и будем греть его, скажем, электрическим нагревателем, то до полного испарения воды нам понадобится 2300 кДж (а не 2300 кДж + 0,1 гПа * 2 м^3 = 2500 кДж)
Избранное
См. также





















Имеется при нормальном давлении:
− 1 кг льда при температуре −100 °С;
− 1 кг воды при температуре 0 °С;
− 1 кг пара при температуре +100 °С.
Всё это смешали в одной ёмкости (в которой тоже поддерживается нормальное давление), пока не установилось тепловое равновесие. Какова окажется температура получившейся смеси?