Центр тяжести и геометрия

Максим Волчкевич
«Квантик» №5, 2023

Исходный текст опубликован в учебнике М.А. Волчкевича «Геометрия. 8 класс» (М.: Просвещение, 2021).

Каждый из вас может проверить: чтобы уравновесить карандаш или линейку на ребре ладони, нужно поместить руку точно под серединой линейки и карандаша. Правда, такое равновесие не всегда будет устойчивым. Ещё со времён Архимеда людям было известно правило рычага. Если два одинаковых груза закрепить на концах прямой палки, а потом середину этой палки поставить на камень, то палка останется в равновесии. А если грузы неодинаковы, то для равновесия палку нужно поставить на камень в такой точке, которая разделит палку в отношении, обратно пропорциональном массам данных грузов (рис. 1). Более строго можно сказать так: произведение массы каждого груза на длину его плеча до опоры на рычаге должно быть одинаковым.

Рис. 1

Если палка с грузами на концах, поставленная на данную точку, останется в равновесии, мы говорим, что в этой точке находится центр её тяжести.

Давайте применим идею центра тяжести в геометрии. При этом мы будем исходить из двух вещей: будем считать, что любая система грузов имеет один центр тяжести и что искать его можно разными способами, группируя данные массы в любом порядке.

Центр тяжести четырёхугольника

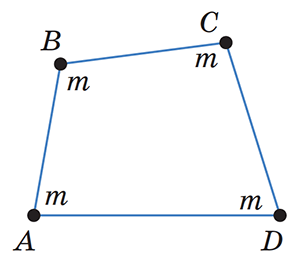
Рис. 2

Давайте найдём центр тяжести системы четырёх одинаковых грузов, которые находятся в вершинах данного четырёхугольника (рис. 2). Поместим в каждую вершину четырёхугольника ABCD одинаковую массу m и будем считать, что его стороны — тонкие невесомые стержни.

Давайте разобьём четыре равные массы в вершинах четырёхугольника ABCD на две пары: две массы на концах его стороны AB и две такие же массы на концах стороны CD. Центр тяжести отрезка AB находится в его середине — можно мысленно заменить две массы на его концах их суммой 2m, находящейся в середине отрезка. Так же сумму масс на концах отрезка CD мы заменим на их сумму 2m и поместим её в его середину (рис. 3).

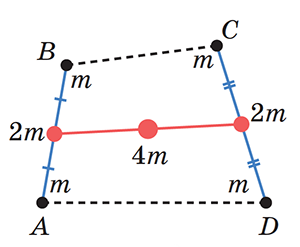
Рис. 3

Где же тогда находится центр тяжести всего четырёхугольника? Если рассуждать по аналогии, то он должен быть в середине отрезка, соединяющего центры масс сторон AB и CD четырёхугольника, то есть в середине его средней линии. Именно туда можно поместить сумму 4m всех масс его вершин.

А теперь самое интересное. Давайте разобьём четыре массы в вершинах четырёхугольника на пары другим способом: сгруппируем массы на концах его стороны BC в середине этого отрезка, а массы на концах стороны AD — в её середине. Тогда центр тяжести всего четырёхугольника должен будет находиться в середине отрезка, соединяющего середины этих сторон. Значит, он лежит на второй средней линии нашего четырёхугольника (рис. 4).

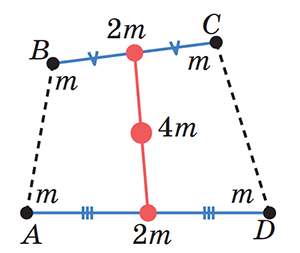
Рис. 4

Что из этого следует? Только то, что средние линии четырёхугольника должны иметь общую середину — делиться точкой пересечения пополам. Этот факт можно доказать и чисто геометрически, он равносилен теореме Вариньона: середины сторон четырёхугольника являются вершинами параллелограмма, а две его средние линии — диагонали этого параллелограмма. Значит, здесь механика отлично согласуется с геометрией.

Рис. 5

Интересно посмотреть, что получится, если начать группировать массы в вершинах четырёхугольника ещё одним способом. Давайте заменим массы на концах каждой его диагонали их суммой 2m, находящейся в середине этой диагонали (рис. 5). Тогда центр тяжести всей системы должен находиться в середине отрезка, соединяющего середины диагоналей четырёхугольника. Конечно, из этого следует, что средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, имеют общую середину.

Рис. 6

Итак, центр тяжести четырёх точек с равными массами лежит на пересечении средних линий четырёхугольника, вершинами которого являются эти точки. Значит, центр параллелограмма Вариньона в четырёхугольнике совпадает с центром тяжести этой системы. Если изготовить четырёхугольник с двумя средними линиями из тонкой проволоки, а во все его вершины поместить одинаковые грузы, то можно будет поставить точку пересечения этих средних линий на остриё иглы, и такая конструкция окажется в равновесии (рис. 6).

Тем же способом можно найти центр тяжести для четырёх неравных грузов, расположенных в вершинах произвольного четырёхугольника.

Центр тяжести треугольника

Теперь тем же механическим методом давайте найдём центр тяжести системы трёх одинаковых грузов.

Мысленно поместим во все вершины произвольного треугольника ABC одинаковые массы m и найдём центр тяжести этой системы. Центр тяжести двух грузов, помещённых в вершины A и C, лежит в середине отрезка между ними. Поэтому данные две массы мысленно можно заменить их суммой 2m, расположенной в середине отрезка AC.

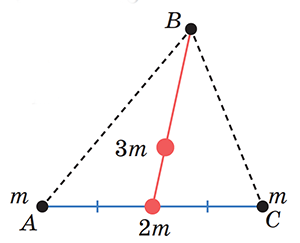
Рис. 7

Как же теперь найти центр тяжести всех трёх масс в вершинах треугольника? Поскольку две из них мы заменили на одну суммарную массу в середине его стороны AC, то нам осталось найти центр тяжести только двух грузов, расположенных на концах данной медианы, проведённой из вершины B треугольника. По правилу рычага этот центр должен лежать на этой медиане и делить её в отношении 2 : 1, то есть обратно пропорционально массам на концах медианы. Именно в этом месте будет сосредоточена суммарная масса 3m всей системы (рис. 7).

Рис. 8

А теперь точно таким же методом давайте заменим массы m в вершинах A и B треугольника на их сумму 2m и поместим её в середину отрезка AB. Тогда центр тяжести всего треугольника будет лежать на медиане, проведённой из его вершины C, и тоже разделит её в отношении 2 : 1 (рис. 8).

Такое же рассуждение можно провести и для третьей медианы треугольника. Значит, центр тяжести всей системы обязан находиться одновременно на всех медианах данного треугольника и делить каждую из них в отношении 2 : 1. Вот почему медианы треугольника должны пересекаться в одной точке (рис. 9).

Рис. 9

Мы убедились, что к теореме о средних линиях четырёхугольника и теореме о медианах треугольника легко можно прийти с помощью соображений классической механики. Многие свои математические открытия великий Архимед делал тоже с помощью правила рычага. Об этом он даже написал целую книгу «Метод механических теорем». Она долгие века считалась навсегда потерянной и была случайно обнаружена на стёртом пергаменте в подвале библиотеки Константинополя только в начале XX века.

Рис. 10

Конечно, мы пользовались тем, что центр тяжести системы не зависит от того, в каком порядке группировать массы её частей. И чтобы рассуждать более строго, нужно это доказать. Но сделать это будет гораздо удобнее, если пользоваться уже не правилом рычага, а складывать векторы.

Если вы вырежете из картона треугольник любой формы, найдёте точку пересечения его медиан и поставите эту точку на остриё вертикальной иглы, то треугольник на ней будет оставаться в равновесии (рис. 10). Это следует из того, что центр тяжести треугольной пластины всегда совпадает с центром тяжести равных масс, расположенных в её вершинах. Но такой же эксперимент с четырёхугольной пластиной произвольной формы у вас уже не получится. И дело здесь в том, что центр тяжести четырёхугольной пластины находится уже не на пересечении её средних линий.

Задачи

Рис. 11

1. В вершинах треугольника поместили массы m, 2m, 3m. Постройте центр масс этого треугольника.

2. Во все вершины пятиугольника поместили равные массы. Как построить центр масс этого пятиугольника?

3. Начертите произвольный четырёхугольник ABCD. Отметьте точку M₁ пересечения медиан треугольника ABC. Проведите отрезок M₁D, как показано на рисунке 11. Теперь отметьте точку M₂ пересечения медиан треугольника BCD и соедините её отрезком с вершиной A. По аналогии проведите отрезки M₃B и M₄C. Какой факт вы заметили? Как бы вы его доказали?

Художник Мария Усеинова