Кратчайшие пути и гипотеза Пуанкаре

Владимир Протасов
«Квант» №11–12, 2020

Управляя каждым шагом,
Повели меня, погнали
Фантастическим зигзагом
По неведомой спирали.

М. Щербаков. Аллилуйя

Геодезические линии

Почему самолет из Москвы в Монреаль летит через Гренландию? Москва находится на 56-й широте, Монреаль — на 45-й, а вся Гренландия — севернее 60-й. Почему самолет туда залетел? А потому, что маршрут стараются проложить по кратчайшему пути по поверхности Земли. А он, как это ни странно, проходит через Гренландию. Часто это противоречит нашей географической интуиции. Кратчайший путь из Екатеринбурга в Лос-Анджелес и вовсе проходит через Северный полюс.

Кратчайший путь по заданной поверхности идет вдоль геодезической линии. Само слово «геодезическая» происходит от науки геодезии, буквально по-гречески γεωδαισία — «деление земли». И если на плоскости геодезические — это прямые, то нахождение геодезических на других поверхностях порой весьма сложно. Величайший математик Леонард Эйлер (1707–1783) в 1732 году вывел общее уравнения геодезических линий. Позже они преобразились в уравнения Эйлера-Лагранжа и стали главным инструментом не только при построении геодезических на поверхностях, но и в других экстремальных задачах. Главным приложением геодезических в то время была картография (отсюда и название). Расстояние между двумя пунктами на карте нужно всегда измерять по геодезической, причем делать это с учетом рельефа местности. Потом геодезические стали применять для построения внутренней геометрии произвольной поверхности, где за расстояние между точками естественно брать кратчайшее расстояние по поверхности. Следует, однако, отличать геодезические линии от кратчайших!

Что такое «геодезическая»? Геодезической на поверхности называется линия, локально кратчайшая в каждой своей точке.

Рис. 1. Геодезическая — локально кратчайшая линия

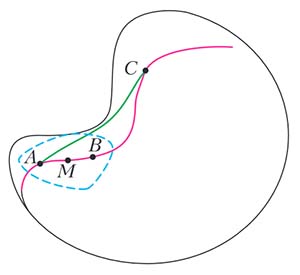
Это значит, что для любой точки M, лежащей на линии, верно следующее: какие ни взять на линии точки A и B, достаточно близкие к M, дуга геодезической AB является кратчайшим путем по поверхности между A и B. Математик сформулирует локально-кратчайшее свойство так: для любых двух точек, лежащих в некоторой окрестности точки M, дуга геодезической является кратчайшим путем по поверхности между ними. Заметим, что кратчайший путь между любыми двумя точками является геодезической линией, но обратное верно не всегда. Красная линия на рисунке 1 — геодезическая, хотя кратчайший путь из точки A в точку C по этой линии не проходит — есть короче. Но для точек, близких к M, все будет хорошо: кратчайший путь будет проходить по геодезической (как между точками A и B на рисунке 1). Например, две близкие точки на сфере соединяются двумя дугами большого круга — длинной синей и короткой красной (рис. 2). Короткая — это кратчайший путь из A в B по сфере. Но и короткая, и длинная — обе — являются геодезическими.

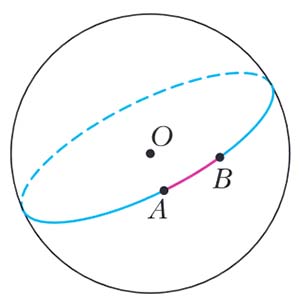
Рис. 2. Геодезические на сфере

Геодезические нужны не только для нахождения кратчайших путей на поверхностях. Именно этим линиям, согласно принципу наименьшего действия Гамильтона, соответствует движение любой механической системы в фазовом пространстве. Любая частица, вынужденная двигаться по поверхности, при этом не подверженная никаким силам, движется вдоль геодезической. В теории относительности движение также происходит по геодезической пространства-времени. Такое же представление имеет теория калибровочных полей.

Все геодезические на плоскости — прямые. На боковой поверхности цилиндра или конуса геодезические построить очень просто — с помощью развертки на плоскость. Геодезические — ровно те линии, которые «распрямляются» при развертке (рис. 3). У сферы, увы, никакой кусок на плоскость не разворачивается. Но геодезические найти легко. Это — дуги больших кругов, т. е. окружностей, получающихся в сечении сферы плоскостями, проходящими через центр. (Будьте внимательны: большой круг — это не круг, а окружность!)

Факт. Все геодезические на сфере — дуги больших кругов.

Рис. 3. Геодезические на цилиндре и на конусе

Доказывается это так же, как и для прямых на плоскости. Сначала надо доказать неравенство треугольника для сферы. Рассмотрим произвольный сферический треугольник, стороны которого — дуги больших кругов. Поскольку длина дуги большого круга пропорциональна углу между радиусами-векторами, будем мерить длины дуг в градусах. Итак:

Неравенство треугольника на сфере. Если все стороны сферического треугольника меньше 180°, то для него выполнено неравенство треугольника.

Доказать это можно так же, как обычное неравенство треугольника на плоскости, — с помощью проекции одной из вершин треугольника на плоскость, содержащую противоположную сторону. Теперь, с помощью неравенства треугольника, доказываем, что любая ломаная на сфере короче дуги, соединяющей концы ломаной. То же, конечно, верно и для любой кривой на сфере. А значит, дуга большого круга (меньшая из двух дуг) является кратчайшим путем между ее концами.

Заметим, что дугами больших кругов являются на сфере не только кратчайшие пути, но и все геодезические линии. Любые две точки на сфере, кроме диаметрально противоположных, соединяют ровно две геодезических. А вся большая окружность — замкнутая геодезическая. Именно с замкнутыми геодезическими нам и предстоит иметь дело.

Три геодезические Пуанкаре. Когда ошибаются гении

Замкнутые несамопересекающиеся геодезические представляют для исследователей особый интерес. Им соответствует периодическое движение механической системы. Есть у замкнутых геодезических и многочисленные геометрические приложения. Мы всегда будем искать только геодезические без самопересечений, и будем в большинстве случаев опускать это длинное слово «несамопересекающаяся».

Рис. 4. Выпуклая поверхность

Поверхность будем всегда предполагать ограниченной и выпуклой. Последнее означает, что ограниченное ею множество выпукло: вместе с любыми двумя своими точками оно содержит и весь отрезок между ними (рис. 4). Для выпуклых поверхностей геодезическую можно представить наглядно: это натянутое на поверхность тонкое резиновое колечко, которое не сползает.

Кроме выпуклости бывает и еще одно предположение — гладкость. Математик скажет, что уравнение, задающее поверхность, имеет вторую непрерывную производную. Для нас будет достаточно такого описания: поверхность не имеет пиков и выступов. Она в самом деле «гладкая», похожая на морскую гальку. Шар и эллипсоид — гладкие поверхности, а многогранник — нет. Для гладких поверхностей верен принцип «локальной единственности» геодезической.

Факт. Две близкие точки на гладкой поверхности можно соединить единственной геодезической линией.

Заметим: не только кратчайшая линия локально единственна, но и геодезическая тоже (в этом случае, она, конечно, и будет кратчайшей). «Две близкие точки» — это значит, что существует такое число r, что между любыми двумя точками на расстоянии не более r есть ровно одна геодезическая. Этот факт сослужит нам хорошую службу и поможет в доказательствах.

В 1905 году великий французский математик Анри Пуанкаре (1854-1912) выдвинул гипотезу о том, что на любой гладкой выпуклой поверхности есть как минимум три замкнутые геодезические. Почему именно три, а не больше? Потому что на эллипсоиде, у которого длины всех осей различны, таких геодезических три — это три его «экватора», т. е. три сечения эллипсоида координатными плоскостями. Напомним (хотя читатель, конечно, это знает), что эллипсоид — это шар, сжатый в трех перпендикулярных направлениях. Его можно задать уравнением

\(\frac{x^{2}}{a^{2}}+\frac{x^{2}}{b^{2}}+\frac{x^{2}}{c^{2}}\geq 1,\)

где a, b, c — положительные числа. Если y=z=0, то x=а или x=−а. Таким образом, ось OX пересекает эллипсоид по отрезку длины 2a — это ось эллипсоида. Всего у эллипсоида три оси, их половины — полуоси, длины полуосей — это a, b и c. Полуоси пересекают поверхность в полюсах, а координатные плоскости — по экваторам.

Экваторы — это геодезические. Каждый экватор эллипсоида является замкнутой геодезической.

В самом деле, возьмем на экваторе две близкие точки M и N. Если кратчайший путь между ними по поверхности эллипсоида не совпадает с дугой MN экватора, то отразим этот путь относительно плоскости экватора. Получим другой путь, тоже кратчайший. Это противоречит единственности.

Итак, разноосный эллипсоид (у которого длины полуосей различны) имеет три замкнутые геодезические — линии экваторов. Пуанкаре предположил, что любое гладкое выпуклое тело будет «не хуже» эллипсоида и тоже будет иметь не меньше трех замкнутых геодезических. Может и больше — шар имеет их бесконечно много. Но три — обязательно! Сам же Пуанкаре доказал свою гипотезу, правда в очень частном случае — для аналитических поверхностей, близких к эллипсоиду. А в общем виде эта проблема долго оставалась нерешенной. Занимались ею многие видные ученые. Крупнейший математик XX века Давид Гильберт (1862-1943) писал об этой задаче в своей книге «Наглядная геометрия», созданной в соавторстве с С. Э. Кон-Фоссеном. Ею занимался один из основателей общей топологии Павел Самуилович Урысон (1898-1924). В 1930 году гипотеза Пуанкаре, наконец, была доказана. Это сделали советские математики Лазарь Аронович Люстерник (1899-1981) и Лев Генрихович Шнирельман (1905-1938), причем для этого они разработали новую теорию топологических методов в вариационных задачах. Ну а гораздо позже, в 1992 году, американские математики Дж. Фрэнкс и В. Бангерт доказали, что на самом деле на любой гладкой выпуклой поверхности существует не три, а бесконечно много замкнутых геодезических.

Стоп, стоп! Как бесконечно много? Мы же знаем, что на эллипсоиде их три! Нет, тут что-то не так. Открываем «Наглядную геометрию» Гильберта и Кон-Фоссена, читаем: «Так можно показать, что на трехосном эллипсоиде единственными замкнутыми геодезическими линиями без самопересечений являются те три эллипса, которые получаются в пересечении этой поверхности с тремя плоскостями симметрии».

Значит, «можно показать». Но авторы не пишут, как именно. Не стали ли они жертвами самообмана, как П. Ферма, которому «не хватило места» на полях книги для доказательства своей Великой теоремы? Ведь согласно теореме Фрэнкса-Бангерта, геодезических бесконечно много на любой гладкой выпуклой поверхности, значит, и на эллипсоиде тоже.

Выходит, Гильберт и Кон-Фоссен ошибались? И Пуанкаре, не ставивший под сомнение, что на разноосном эллипсоиде их ровно три? И Урысон, и Люстерник, и Шнирельман — все они ошибались? Да! Более того, все они прошли мимо элементарного примера «четвертой» геодезической на эллипсоиде. Пример этот появился в 1982 году в книге В. Клингенберга «Riemannian geometry», а потом еще многократно переоткрывался¹.

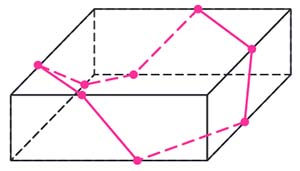
Рис. 5. Перевязочная лента

Четвертая геодезическая на эллипсоиде. Пример этот настолько наглядный и замечательный, что его можно разбирать на уроках в школе. Все видели, как перевязывают коробки с конфетами: пускают часть ленты внизу, по дну коробки, затем ведут наверх, по крышке, затем опять спускают вниз и затем опять наверх. Получается линия из четырех частей — две противоположные части внизу и две наверху (рис. 5). А теперь надо сделать то же, но не на прямоугольной коробке, а на круглой. Сейчас мы построим эту линию на эллипсоиде.

Возьмем эллипсоид, у которого одна ось сильно меньше двух других. Почти плоский. Обозначим концы длинных полуосей (в порядке следования) A, B, C, D. Соединим A и B кратчайшей линией, идущей по поверхности эллипсоида. Так как эллипсоид почти плоский, эта линия будет близка к отрезку AB и уж точно не будет идти по экватору, потому что длина дуги экватора больше отрезка АВ. Теперь проведем такую же дугу AD по другой (нижней) стороне эллипсоида. Иначе говоря, дуга AD переходит в дугу AB при повороте на 180° относительно оси AC. Далее пустим такую же дугу DC по верхней стороне и закончим дугой CB с нижней стороны.

Мы получили замкнутую линию, состоящую из четырех равных дуг (рис. 6). Оказывается, она будет геодезической.

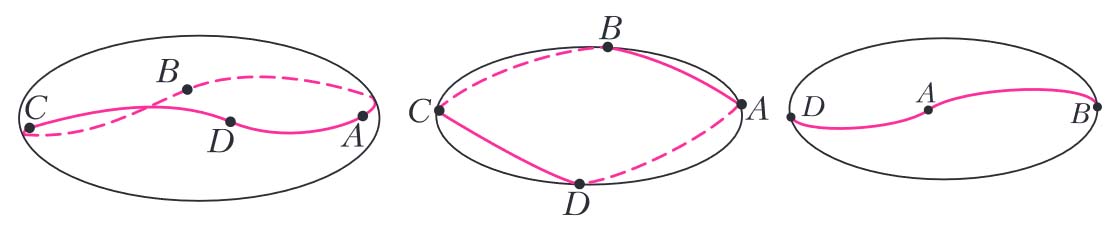
Рис. 6. «Четвертая» геодезическая на эллипсоиде

Теорема 1. Построенная замкнутая линия ABCD является геодезической на поверхности эллипсоида.

Доказательство. В каждой внутренней точке дуги AB линия является локально кратчайшей. Если нет, просто заменим ее маленький кусочек на более короткий и получим более короткий путь из A в B, что невозможно. Так же — с тремя другими дугами. Таким образом, во внутренних точках дуг все хорошо. Проблема возникает на концах дуг. Почему, скажем, в точке A наша линия локально кратчайшая? Возьмем рядом с A две точки M и N на разных дугах. Почему путь MN вдоль линии является кратчайшим на эллипсоиде? Из построения этого не следует.

Рис. 7

Предположим, что дуга AM длиннее дуги AN. Тогда возьмем на продолжении дуги AN за точку N точку M', для которой дуга AM' равна дуге AM (рис. 7, а). Ясно, что M и M' переходят друг в друга при повороте на 180° относительно оси AC. Если дуги AM и AN равны, то просто обозначим M'=N. Теперь предположим обратное: есть более короткий путь на поверхности эллипсоида между точками M и N. Добавив к этому пути дугу NM', получаем более короткий путь по поверхности между M и M'. Значит, кратчайший путь между M и M' не совпадает с дугой нашей линии MM'. Сделаем поворот на 180° относительно оси AC. Точки M и M' поменяются местами, а кратчайший путь между ними должен перейти в себя — ведь он единственный! Обозначим через P середину этого кратчайшего пути (расстояния меряются вдоль пути). Поворот на 180° относительно оси AC оставляет эту точку на месте. Но тогда она лежит на оси вращения — прямой AC. А поскольку она находится на поверхности эллипсоида, она совпадает либо с A, либо с C. До точки C слишком далеко, кратчайший путь туда не заходит. Значит, P=A. Итак, середина кратчайшего пути из M в M' находится в точке A (рис. 7, 6). Значит, кратчайший путь из A в M идет по нашей линии. Иначе, поставим его вместо дуги AM и тем самым уменьшим длину дуги AB, что невозможно. Значит, и кратчайший путь из M в M' идет по нашей линии, что противоречит предположению. Теперь все доказано.

Ну вот, а обещали совсем элементарный пример... А он потребовал довольно тонкого рассуждения. Да, но это — для доказательства. А построение этого примера действительно очень просто. Если учитель младших классов даст ребятам подобный плоский эллипсоид и попросит натянуть на него резиновое колечко иначе, чем вдоль одного из трех экваторов, они несомненно справятся. Зацепить петлей сверху, продеть внизу, затем — другой петлей сверху. Тем удивительнее, что мнгие десятилетия никто не додумался до этого примера. И никто, включая крупнейших математиков XX века — Пуанкаре и Гильберта, не допустил мысли, что на эллипсоиде может быть четвертая геодезическая. Чудеса случаются!

На самом деле это — не единственный пример «неправильной» геодезической на эллипсоиде. Есть еще. В упражнении 5 мы предлагаем вам их построить. А нас ждут многогранники!

Продолжение следует.

¹ Например, его в 2004 году независимо придумал российский математик С. С. Анисов, который и сообщил его автору. Лишь значительно позже мы узнали, что такой же пример содержится в книге Клингенберга.