Закрыть

Меню

Библиотека > В популярных журналах > «Квантик»

Изобретая логарифмическую линейку

«Квантик» №2, 2022 • Математика • Комментировать

Виктор Клепцын
«Квантик» №2, 2022

До середины XX века логарифмическая линейка была непременной принадлежностью инженера. Она позволяла быстро выполнять различные действия — умножать, возводить в степень и многое другое, что сейчас для нас делает компьютер, калькулятор или приложение на телефоне.

А как она была устроена? Чтобы разобраться, воспользуемся наиболее надёжным способом — придумаем её сами, — а заодно научимся с ней обращаться.

Механическое сложение

Начнём с гораздо более простого вопроса: а как нам сделать что-нибудь, что позволяло бы одним движением складывать (небольшие) числа?

Представим себе, что мы взяли две (настоящие, деревянные) линейки, причём на одной из них шкала у верхней границы (как это обычно бывает), а на другой у нижней (а вот так почти никогда не бывает, но можно же и самим перенести деления с одной линейки на другую!). Приложим их друг к другу так, чтобы совпали нули — тогда шкалы на них совпадают.

Сдвинем нижнюю линейку вправо — скажем, на 2 см (рис. 1, в центре) Что будет напротив отметки «3 см» на той же линейке? Это отметка на расстоянии 3 см от нуля на нижней линейке, который сам отстоит на 2 см от нуля на верхней. Значит, всего эта отметка отстоит на 2 см+3 см=5 см от нуля на верхней линейке, и напротив отметки в «3 см» мы видим отметку «5 см».

Рис. 1. Сложение с помощью двух линеек

Ура! Всего лишь с помощью абзаца рассуждений и двух линеек мы научились механически складывать 2 + 3 и получать в ответе 5. Но лиха беда начало!

А как складывать двузначные числа? Да точно так же! На линейке ведь есть ещё и миллиметровая шкала. И можно сказать, что 16 + 27 = 43, можно, что 16 мм + 27 мм = 43 мм, а можно, что 1 см 6 мм + 2 см 7 мм=4 см 3 мм (рис. 1, справа).

Ну хорошо. Мы научились механически, сдвигом линейки, складывать одно- и двузначные числа. Но трудно-то умножать! Как бы нам и эту операцию переложить на нашего механического помощника?

Умножение степеней 10

Сначала научимся умножать друг на друга не любые числа, а только 10, 100, 1000 и т. п. Не то чтобы это сложно: когда мы умножаем друг на друга числа вида «единица и сколько-то нулей», нужно просто сложить количество нулей: скажем, 100×1 000=100 000.

Постойте, сложить? Так это мы уже умеем! Возьмём нашу линейку и вместо деления «1 см» поставим 10, вместо деления «2 см» поставим 100, вместо «3 см» поставим 1000 и т. п. И вместо нулевого деления поставим «единицу с нулём нулей», то есть просто 1. Но вот куда поставить другие числа, чтобы выполнять умножение таким же сдвигом линеек?

Рис. 2. Умножение степеней 10

Давайте сформулируем явно, что именно должно выполняться: если на расстоянии r см стоит число a, а на расстоянии s см стоит число b, то на расстоянии r+s см должно стоять число a ⋅ b. Обозначим расстояние, на котором мы поставим число a, довольно длинным образом — как $\log_{10}a$. Тогда нам нужно, чтобы выполнялось соотношение

$\log_{10}ab$=$\log_{10}a$ ⋅ $\log_{10}b$. (1)

А можно ли такие расстояния $\log_{10}a$ подобрать для всех чисел a, а не только для степеней 10 — которые мы уже расставили, поставив число

$1\hspace{-3pt}\underbrace{0 \ldots0}_{\mbox{$r$ нулей}}=$ $\underbrace{10×⋅⋅⋅×10}_{\mbox{$r$ десяток}}=10^r$

на расстоянии $\log_{10}10^r$ = r см? Оказывается, что можно, и мы научимся это делать. Такой способ расставлять числа называется логарифмической шкалой (рис. 3), а функция $\log_{10}$ — десятичным логарифмом.

Рис. 3. Логарифмическая шкала

Но прежде чем выяснять, как именно такую функцию $\log_{10}$ строить, давайте воспользуемся готовым результатом (таблицей или файлом со шкалой) и сделаем «демоверсию» логарифмической линейки своими руками!

Рис. 4. Логарифмическая линейка: принцип работы

Настоящая логарифмическая линейка

В настоящей логарифмической линейке обычно её подвижная часть вставляется в жёлоб в неподвижной части, чтобы легко вдоль неё скользить, не выпадая (рис. 5, справа). Самому сделать такое из дерева не очень просто, но для демонстрации принципа можно сделать её и из бумаги, обернув неподвижную часть вокруг подвижной (рис. 5, слева), распечатав заготовку по ссылке kvan.tk/rule (попробуйте!).

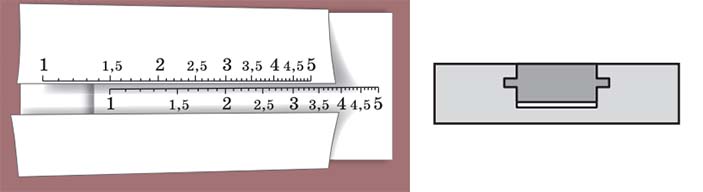
Рис. 5. Слева: самодельная логарифмическая линейка; справа: логарифмическая линейка в разрезе (один из вариантов конструкции; подвижная часть выделена тёмным цветом)

А ещё можно такую шкалу нанести самостоятельно — воспользовавшись таблицей логарифмов, компьютером или инженерным калькулятором (одна из функций, которые любой инженерный калькулятор умеет вычислять, — это логарифм)¹.

Как можно увидеть на фотографии (рис. 6), настоящая логарифмическая линейка сложнее, чем наше простое описание: на ней значительно больше шкал, и благодаря этому она позволяет легко выполнять значительно больше операций.

На этой фотографии видны шкалы A (на неподвижной части) и B (на подвижной) — это те самые логарифмические шкалы. Сдвиг подвижной части и позволяет легко умножать (и делить!) числа. Но что, если нам часто приходится возводить числа в квадрат? Можно каждый раз умножать число само на себя, a²=a · a, сдвигая 1 на подвижной части к a и читая ответ напротив отметки a на подвижной части. А можно заметить, что

$\log_{10}a^{2}$=$\log_{10}a$ + $\log_{10}a$=2$\log_{10}a$. (2)

Рис. 6. Логарифмическая линейка: шкалы и нить. Мелкие цифры 1, 2, 3 ... на шкале D отмечают десятые доли, то есть это деления 1,1; 1,2; 1,3...

На фотографии видна шкала D — это логарифмическая шкала A, растянутая в два раза. И это позволяет возводить числа в квадрат одним движением прозрачного ползунка с нитью (применяемого для точного сопоставления чисел на разных шкалах): напротив числа a на шкале D мы видим на шкале A число a². А чтобы извлечь из числа b квадратный корень, нужно найти число b на шкале A; напротив него на шкале D и будет искомый корень $\sqrt{b}$ (например, напротив 2, записанного на шкале A, стоит на шкале D число, чуть большее 1,4).

А что, если мы хотим возвести число в третью или в пятую степень? Аналогично (2),

$\log_{10}a^{3}$=$\log_{10}(a · a2)$ = $\log_{10}a$ + $\log_{10}a^{2}$
= $\log_{10}a$ + 2$\log_{10}a$ = 3$\log_{10}a$,

и вообще

$\log_{10}a^{n}$=$\textit{n}$$\log_{10}a$. (3)

Поэтому n-ю степень числа a можно вычислить так: сначала вычислить логарифм a, потом умножить его на n — и результатом будет логарифм aⁿ. И тут нам нужно умножать на n.

Стоп, умножать? Так мы это уже научились делать быстро — как раз с помощью логарифмов! Давайте применим (ещё раз!) логарифм к равенству (3): получаем

$\log_{10}$($\log_{10}a^{n}$)=$\log_{10}$($\textit{n}$$\log_{10}a$)=$\log_{10}a^{n}$+$\log_{10}$($\log_{10}a$).

Поэтому — если поставить каждое число a на расстоянии $\log_{10}$($\log_{10}a$) на ещё одной шкале, то мы сможем вычислять aⁿ, просто сдвигая относительно этой шкалы обычную логарифмическую (рис. 7).

Рис. 7. Возведение в степень

Так вот — на некоторых шкалах (их часто подписывают символами LL, см. рис. 6) число a стоит на расстоянии в $\log_{10}$($\log_{10}a$) единиц длины². И теперь мы знаем зачем — чтобы легко возводить числа в степени!

Упражнение. На рисунке 8 отмечены 1, 8 и 25 на логарифмической шкале. С помощью обычной линейки отметьте на этой же шкале числа 200, 64, 5, 2, 10, $\sqrt{2}$, 0,5. Где располагается число 15, ближе к 8 или к 25?

Рис. 8

Художник Алексей Вайнер.

Окончание следует.

¹ Ещё симулятор логарифмической линейки есть на сайте «Математических этюдов». Но сделать своими руками всё-таки интереснее!

² Везде выше мы писали о десятичном логарифме, просто потому, что мы естественно придумали именно его. Но логарифмы бывают не только десятичные — и об этом мы поговорим в следующий раз.

Написать комментарий