Квантик, Ноутик и фигурные преобразователи

Александр Перепечко
«Квантик» №4, 2021

— Квантик, да здесь целый склад фигурных преобразователей!

— Давай опробуем их в действии!

Вот так Квантик и Ноутик, забравшись на заброшенный чердак, принялись исследовать диковинные устройства — фигурные преобразователи.

Рис. 1

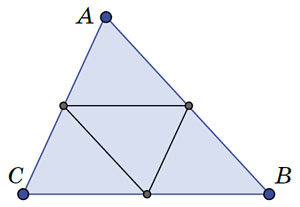
— Смотри, Квантик, этот — самый простой. Если ему дать треугольник ABC, он разделит его стороны в отношении 1:1, то есть пополам, и выдаст новый треугольник с вершинами в полученных точках (рис. 1).

— Ага, новый треугольник будет такой же, как прежний, но в 4 раза меньше по площади. — Квантик уже скормил преобразователю треугольник и показал Ноутику, как исходный треугольник складывается из четырёх копий полученного. — Видишь, стороны нового треугольника — это средние линии исходного, то есть они соединяют середины его сторон.

— Так-так... средняя линия треугольника параллельна соответствующей стороне, — припомнил Ноутик, — и в два раза короче её!

— И поэтому новый треугольник имеет такие же углы, но в два раза меньшие стороны.

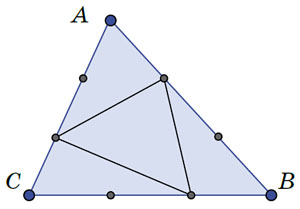
Рис. 2

— Ну да... — немного разочарованно протянул Ноутик и перешёл к следующему. — А вот преобразователь поинтересней! Он делит стороны треугольника уже в отношении 1:2 (рис. 2).

— Да, здесь треугольник делится уже не на одинаковые части. Но у нового треугольника площадь меньше ровно в три раза!

И Квантик пустился в пространные объяснения. Полчаса спустя Ноутик всё же понял ключевое утверждение Квантика: если два треугольника имеют общий угол, то их площади соотносятся так же, как произведения прилегающих к этому углу сторон.

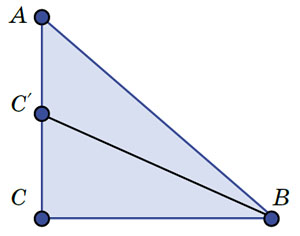
Рис. 3

Задача. Докажите утверждение Квантика, используя такой факт: отношение площадей треугольников ABC и ABC′, где C′ лежит на AC (рис. 3), равно отношению AC к AC′.

— Ага, — наконец просветлел Ноутик. — При преобразовании от АВС отрезали три угловых треугольника, каждый площадью \( \frac{1}{3} · \frac{2}{3} = \frac{2}{9} \) площади АВС, суммарно — \( \frac{6}{9} \), и остался огрызок как раз в \( \frac{1}{3} \) площади АВС. Интересно, а полученный треугольник будет с такими же углами, как и АВС?

— Наверное, не всегда, — предположил Квантик. — Ладно, пошли вон к тем, совсем заковыристым преобразователям. Им нужно давать четырёхугольники!

— О, вот этот опять делит стороны пополам. Получается четырёхугольник, совсем не похожий на исходный (рис. 4). А какая у него площадь?

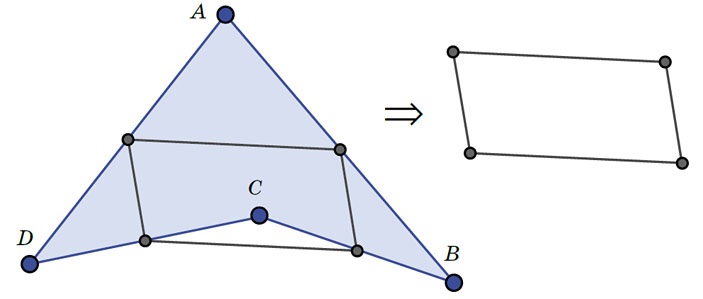
Рис. 4

Рис. 5

— Используем такой трюк: если в исходном четырёхугольнике ABCD сдвинуть одну диагональ (AC) вдоль самой себя, а другую (BD) оставить на месте, получится четырёхугольник A′BC′D той же площади (рис. 5). Как бы это тебе попроще объяснить...¹

— Ну уж нет, ещё час я слушать не намерен! — возмутился Ноутик.

— Это очень красиво! — запротестовал Квантик, но, смирившись, решил объяснить в следующий раз и продолжил: — Сдвигая диагонали таким образом, мы можем превратить ABCD в параллелограмм.

— Надо же! А преобразованный четырёхугольник при этом вообще не меняется — только двигается.

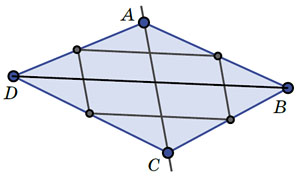
Рис. 6

— Ну естественно! Его стороны, как средние линии, параллельны диагоналям и вдвое меньше по длине, — пояснил Квантик (рис. 6).

— А значит, его площадь вдвое меньше параллелограмма АВСD, ура! — возликовал Ноутик. — Ух ты, а это что за экземпляр?

— Он тоже преобразует четырёхугольники, но стороны AB и CD он делит в отношении 1:2, а стороны BC и DA — в отношении 2:1.

— Какой странный преобразователь! Во сколько же раз будет меньше полученный четырёхугольник? И обязательно ли он будет меньше?

Правильно ответив на последний вопрос Ноутика, вы решите задачу 40 «Нашего конкурса» на с. 32, а также догадаетесь, почему на чердаке не было преобразователя, делящего стороны четырёхугольника в одном и том же отношении 1:2.

Художник Екатерина Соловей

¹ См. статью Г. Мерзона «Площади и перекашивания» в «Квантике» №2 за 2020 год.