Прорыв в задаче о раскраске плоскости

Андрей Райгородский, Всеволод Воронов, Савватеев Алексей
«Квант» №11, 2018

Введение

В этой статье мы расскажем о недавнем удивительном продвижении в одной из самых известных задач комбинаторной геометрии. Это задача о так называемом хроматическом числе плоскости. Требуется найти минимальное число цветов, в которые можно так покрасить плоскость, чтобы расстояние между точками одного цвета никогда не равнялось единице. Это число и называется хроматическим, а обозначается оно \( χ (\mathbb{R}^2) \). Зачем так много букв? Ну, просто красить можно не только плоскость — можно и прямую, и пространство, и многие другие интересные объекты. На прямой, кстати, все почти очевидно: \( χ (\mathbb{R}^1) = 2 \), так как одного цвета, конечно, не хватит, а двух достаточно, о чем свидетельствует рисунок 1. Что же с плоскостью?

Рис. 1. Раскраска прямой в 2 цвета

Рис. 2. Мозеровское веретено

Ясно, что не хватит одного цвета, и легко видеть, что не хватит и двух цветов. Действительно, рассмотрим вершины правильного треугольника со стороной 1. Уже для «правильной» раскраски этих трех точек, очевидно, необходимо использовать три различных цвета. Чуть более сложная конструкция так называемого мозеровского веретена (рис. 2) показывает, что \( χ (\mathbb{R}^2) ≥ 4 \).

В то же время легко покрасить плоскость в 7 цветов без точек одного цвета на расстоянии 1. Целых две разных покраски изображены на рисунках 3 и 4. На рисунке 3 цвета образуют правильные шестиугольники с большими диагоналями длины x чуть меньше единицы. Границы между двумя или тремя шестиугольниками красятся в цвет любого из них (в любой из двух или трех цветов, соответственно, но не в один из оставшихся цветов). Расстояния между ближайшими шестиугольниками одного цвета равны \( x \frac{\sqrt{7}}{2} \), и это число, в свою очередь, должно быть уже строго больше единицы. Таким образом, кажется, что у раскраски есть «запас прочности», позволяющий как-то ее модифицировать в раскраску шестью цветами. На рисунке 4 цвета образуют квадраты, и здесь никакого запаса прочности нет, даже границы приходится красить с осторожностью¹.

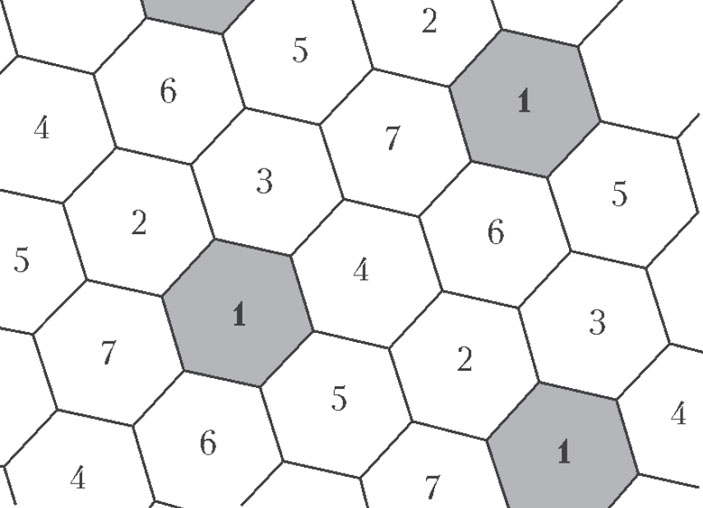
Рис. 3. Первая раскраска плоскости в 7 цветов

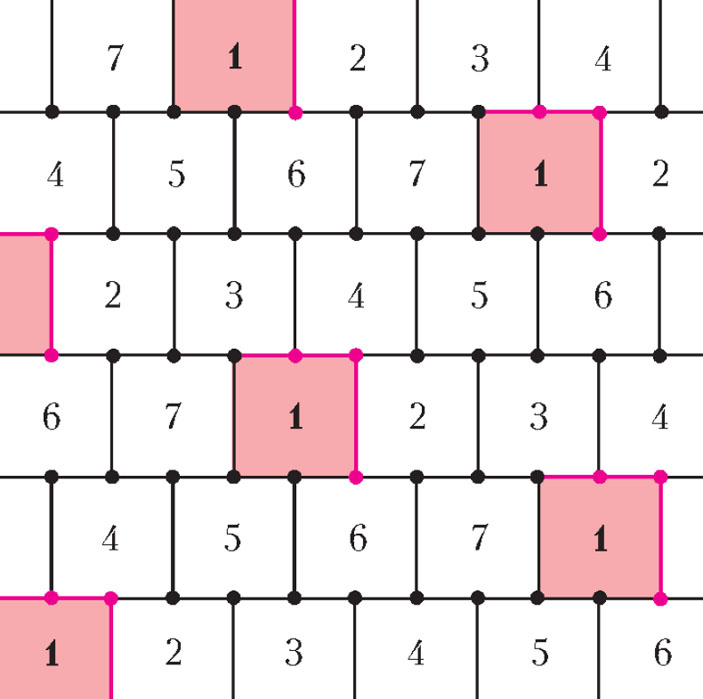
Рис. 4. Вторая раскраска плоскости в 7 цветов

Задача об отыскании хроматического числа плоскости возникла в 1950 году (см. [1]), хотя еще в 1944 году очень близкую задачу изучал Хадвигер. До недавнего времени все, что было известно о хроматическом числе, — это с легкостью доказанные нами только что оценки

\( 4 ≤ χ (\mathbb{R}^2) ≤ 7 \).

Иными словами, около 70 лет в крайне популярной задаче было целых 4 варианта ответа, и никаких продвижений к установлению истины не было!

Отметим ряд интересных смежных фактов. Например, все нижние оценки, которые мы получали, это фактически оценки с помощью графов. И треугольник, и мозеровское веретено — это так называемые дистанционные графы, т.е. графы, вершины которых — точки плоскости, а ребра — отрезки длины 1, соединяющие пары точек, отстоящих друг от друга на расстояние 1. Напомним, что хроматическое число графа G — это минимальное число цветов \( χ(G)\), в которые можно так покрасить вершины графа, чтобы концы любого ребра имели разные цвета. Таким образом, \( χ (\mathbb{R}^2) ≥ χ(G) \) для любого дистанционного графа G. В 1976 году Эрдёш поставил вопрос, существуют ли дистанционные графы с хроматическим числом 4 (как у мозеровского веретена), но без треугольников. Оказалось, и такое бывает! Сейчас известны примеры всего лишь на двадцати трех вершинах (см. [2]).

В 1971 году Вудалл доказал, что если красить плоскость в некотором смысле так же, как на рисунках 3 и 4, то потребуется не меньше шести цветов. Что значит «так же»? Ну, скажем, каждый цвет — это объединение некоторого числа многоугольников (не обязательно выпуклых и не обязательно содержащих всю свою границу). Получается, что если вдруг \( χ (\mathbb{R}^2) < 6 \), то раскраску и представить себе трудно!

В 2016 году Канель-Белов предложил [4] следующую интерпретацию задачи. Рассмотрим в трехмерном пространстве слой между двумя плоскостями толщины ε. Понятно, что при достаточно малых ε запас прочности с рисунка 3 позволяет и весь слой покрасить в 7 цветов без точек одного цвета на расстоянии 1. Оказалось, что при любом ε > 0 четырех цветов уже не хватает: нужно хотя бы 5! Иными словами, если вдруг \( χ (\mathbb{R}^2) = 4 \), то раскраску не просто трудно, а запредельно трудно себе представить!

Многие другие любопытные факты можно найти в книгах [1] и [3].

А 8 апреля 2018 года случилось замечательное событие. На ресурсе arxiv.org, куда выкладываются статьи до своей публикации в журналах, появилась заметка Обри ди Грея [5], в которой описывался дистанционный граф с хроматическим числом 5! Поскольку задача невероятно популярна, огромное количество специалистов взялось за проверку и практически сразу результат был подтвержден. Теперь мы знаем, что

\( 5 ≤ χ (\mathbb{R}^2) ≤ 7 \).

Интересно, что ди Грей не является профессиональным математиком. Он геронтолог по специальности, т.е. он занимается изучением процессов старения. Свежий взгляд на задачу позволил ему добиться такого успеха.

В работе ди Грея дистанционный граф с хроматическим числом 5 имел 1581 вершину. Сейчас уже найдены графы с 553 вершинами [6]. И есть смельчаки, надеющиеся отыскать графы с хроматическим числом 6!

В настоящей статье мы расскажем о том, как получается результат ди Грея.

О пользе свежего взгляда

Посмотрим, как устроены самые простые дистанционные графы с хроматическим числом 4. Это веретено Мозеров, изобретенное братьями Лео и Вильямом Мозерами, и граф Голомба. В веретене Мозеров есть два подграфа-«ромба», состоящих из двух равносторонних треугольников с общей стороной. При любой раскраске вершин такого подграфа в 3 цвета точки M, N имеют один цвет (рис. 5, а). Значит, в веретене Мозеров точки P, Q, R одного цвета, но Q и R соединены ребром (рис. 5, б). Можем ли мы получить противоречие таким же способом, когда цветов не три, а четыре? Другими словами, построить такой граф, что в нем есть пара вершин, цвета которых совпадают при любой правильной раскраске. Тогда было бы доказано, что плоскость не красится в четыре цвета. Но как построить такой граф — непонятно.

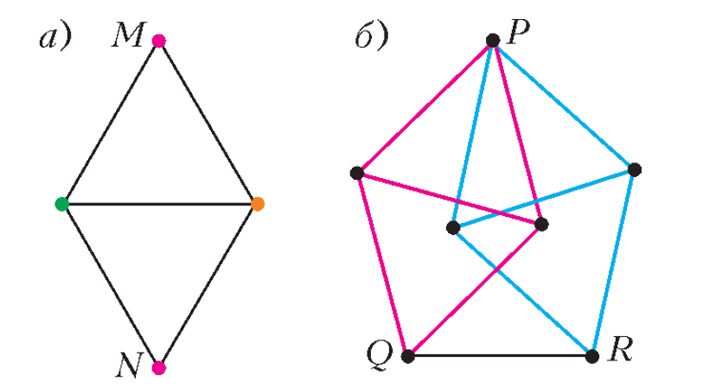
Рис. 5. Подграфы в веретене Мозеров

Разобьем граф Голомба на два подграфа (рис. 6, а). Первый из них — шестиугольник, содержащий шесть равносторонних треугольников. С точностью до перестановок цветов он красится в три цвета единственным образом (рис. 6, б) Значит, вершины равностороннего треугольника A′B′C′ со стороной \( \sqrt{3} \) раскрашены в этом случае в один цвет.

Рис. 6. Подграфы в графе Голомба

Обозначим здесь и далее \( Δ_{\sqrt{3}} \) — множество, состоящее из вершин равностороннего треугольника со стороной \( \sqrt{3} \). При этом расположение треугольника на плоскости может быть любым.

Во втором подграфе вершины такого равностороннего треугольника соединены с вершинами равностороннего треугольника со стороной 1 (рис. 6, в). При раскраске в три цвета точки X, Y, Z разноцветные. Тогда A″, B″, C″ не могут быть одного цвета, поскольку он совпадет с цветом одной из точек X, Y, Z. Таким образом, в графе Голомба к противоречию приводит раскраска двух подграфов: первый из них гарантирует, что вершины \( Δ_{\sqrt{3}} \) будут одноцветными, а второй исключает такую возможность.

Теперь нас интересует дистанционный граф, который невозможно раскрасить в четыре цвета. Может быть, проще искать не весь граф целиком, а подграфы, раскраска которых приводит к противоречиям? В первом подграфе некоторый набор вершин, «шаблон», при любой правильной раскраске будет одноцветным, а во втором подграфе он всегда разноцветный. Или так: если в первом подграфе найдется хотя бы один одноцветный шаблон, а во втором подграфе его невозможно покрасить в один цвет, то это непременно приведет к противоречию при раскраске плоскости. (С одной стороны, одноцветный шаблон должен где-то обнаружиться, а с другой стороны, он запрещен — ведь к любому его расположению на плоскости можно прикрепить второй граф.)

Именно так и действовал ди Грей: он рассматривал в качестве шаблона треугольник \( Δ_{\sqrt{3}} \), как в графе Голомба, и перебирал раскраски в 4 цвета двух довольно сложных дистанционных графов, о которых речь пойдет далее.

Построение графа, содержащего одноцветный \( Δ_{\sqrt{3}} \)

В каких множествах точек среди попарных расстояний встречается много единиц, а среди всевозможных треугольников — много \( Δ_{\sqrt{3}} \)? Первое, что приходит в голову, это кусок треугольной решетки. Рассуждая от противного, предположим, что одноцветный треугольник \( Δ_{\sqrt{3}} \) отсутствует. Это не приводит к противоречию сразу, но сильно ограничивает число возможных раскрасок.

Упражнения

1. Убедитесь, что если правильная раскраска в 4 цвета графа на рисунке 7 не содержит одноцветного \( Δ_{\sqrt{3}} \), то: а) каждый цвет, кроме цвета центральной вершины, встречается ровно два раза; б) с точностью до поворотов и перестановок цветов допустимы только две раскраски.

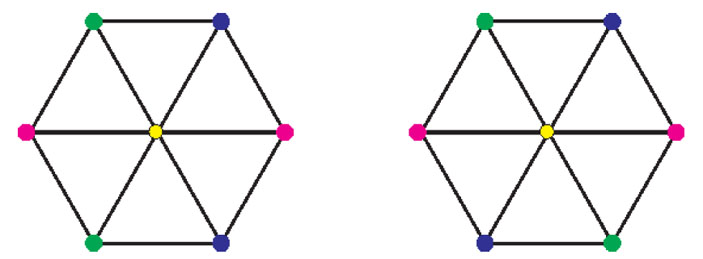
Рис. 7. Раскраски графа на 7 вершинах

2. Докажите, что всякая раскраска треугольной решетки в 4 цвета, не содержащая одноцветного \( Δ_{\sqrt{3}} \), состоит из чередующихся линий сетки, на каждой из которых есть вершины только двух цветов.

Указание. Можно рассмотреть два случая: а) в шестиугольниках встречается только раскраска, приведенная на рисунке 7 справа; б) хотя бы в одном шестиугольнике встречается тип раскраски, как на рисунке 7 слева.

Рис. 8. Граф Q

Возьмем участок треугольной решетки в форме цветка (рис. 8) и назовем этот граф Q. С точностью до поворотов и перестановок цветов существует шесть раскрасок центрального большого шестиугольника без одноцветного \( Δ_{\sqrt{3}} \) (рис. 9). Цвета двенадцати крайних вершин нам не интересны, хотя их наличие влияет на число вариантов раскраски. Важно, что в раскрасках a, г все вершины шестиугольника раскрашены в тот же цвет, что и его центр; в раскрасках б, д таких вершин четыре, а в раскрасках в, е только две.

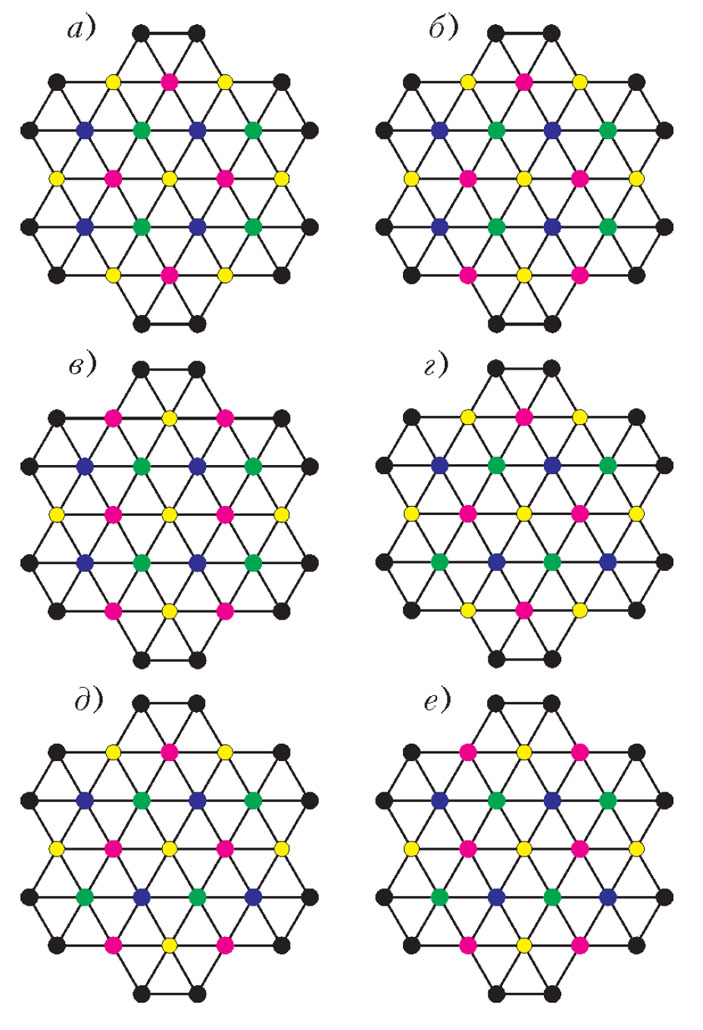
Рис. 9. Возможные раскраски центральной области в графе Q

Рис. 10. Граф X состоит из двух экземпляров графа Q с общей центральной вершиной

Что будет, если взять два экземпляра графа Q₁ и Q₂ с общей центральной вершиной и повернуть один из них на угол \( α = 2 \text{arcsin} \frac{1}{4} \) относительно другого (рис. 10)? В получившемся графе, обозначим его X, расстояния между соответствующими вершинами шестиугольников равны единице:

AA′ = BB′ = CC′ = DD′ = EE′ = FF′ = 1.

Кроме того, в каждом из экземпляров графа Q две, четыре или шесть вершин шестиугольника раскрашены в тот же цвет, что и центральная. Если хотя бы в одном из экземпляров таких вершин четыре или шесть, то найдутся две вершины одного цвета на расстоянии 1. Следовательно, в Q₁ и Q₂ допустимы лишь раскраски в, е.

Наконец, заметим, что в раскрасках в, е концы диагоналей шестиугольников раскрашены одинаково. Поэтому в графе X при дополнительном условии об отсутствии одноцветного \( Δ_{\sqrt{3}} \) вершины A, D имеют один цвет — почти как в трехцветной раскраске веретена Мозеров. Возьмем два экземпляра графа X, совместим их и повернем один из них относительно другого вокруг A на угол \( β = 2 \text{arcsin} \frac{1}{8} \). Тогда \( D\tilde{D} = 1 \) и эти вершины раскрашены в тот же цвет, что и A. Мы пришли к противоречию, а значит, построен граф G, в котором хотя бы один треугольник \( Δ_{\sqrt{3}} \) раскрашен в один цвет (рис. 11).

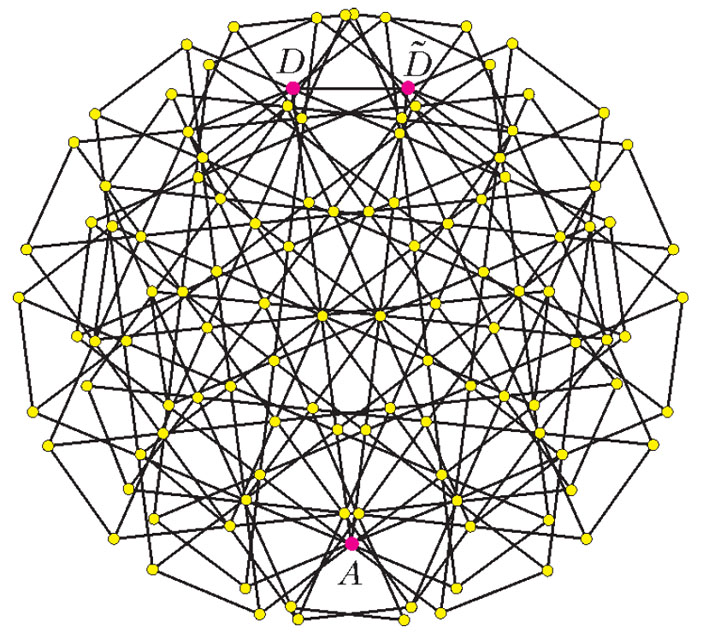
Рис. 11. Граф G, в свою очередь, состоит из двух экземпляров графа X

Упражнение 3. Докажите, что если множество узлов треугольной сетки размножить тремя поворотами на углы α, β, α вокруг одного и того же узла, получая при этом еще три экземпляра сетки (рис. 12), то полученный бесконечный дистанционный граф при любой раскраске узлов в 4 цвета также содержит одноцветный \( Δ_{\sqrt{3}} \). Как и выше, \( α = 2 \text{arcsin} \frac{1}{4} \), \( β = 2 \text{arcsin} \frac{1}{8} \).

Рис. 12. Четыре экземпляра треугольной сетки

Построение графа, исключающего раскраску \( Δ_{\sqrt{3}} \) в один цвет

Правильность описанного выше построения можно проверить если не в уме, то хотя бы с ручкой и листком бумаги. К сожалению, второй граф из статьи ди Грея не допускает наглядных объяснений. Пока никто не придумал, как доказать без компьютера, что этот граф обладает нужным свойством, или как построить другой граф, для которого доказательство было бы «человеческим» от начала до конца.

Ди Грей предположил, что если в дистанционном графе содержится достаточно много веретен Мозеров в качестве подграфов, то удастся исключить одноцветную раскраску хотя бы одного фиксированного треугольника \( Δ_{\sqrt{3}} \). Как построить такой дистанционный граф, чтобы на одну вершину в среднем приходилось как можно больше веретен? После ряда неудачных попыток ди Грей пришел к конструкции, при описании которой пригодится следующее определение.

Определение. Пусть X, Y — некоторые множества векторов (вообще говоря, X, Y могут состоять из чего угодно, лишь бы была определена операция сложения). Суммой Минковского M = X + Y называется множество, состоящее из всех возможных сумм x + y, где x ∈ X, y ∈ Y (см. пример на рисунке 13).

Рис. 13. Сумма Минковского {u₁, u₂} + {v₁, v₂, v₃}

Иногда мы будем говорить о сумме Минковского дистанционных графов, имея в виду граф, вершины которого — сумма множеств вершин слагаемых, а ребра — всевозможные отрезки единичной длины.

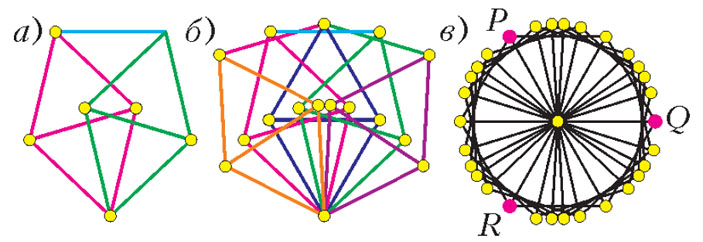
Рис. 14. Классы эквивалентности ребер. Граф V

На рисунке 14, б совмещены «обычное» веретено Мозеров (рис. 14, а) и «тройное» веретено — два веретена Мозеров с общим подграфом-«ромбом». Назовем два ребра эквивалентными, если угол между ними кратен 60°. Ребра разобьются на 5 классов, отмеченных цветом (см. рис. 14, б). Сопоставим каждому ребру вектор, приписав ему произвольное направление. Теперь представим, что на плоскости сидит кузнечик и он может прыгать на единичное расстояние или в одном из этих направлений, или в любом из них, повернутом на угол, кратный 60°. Отметим начальную точку и все точки, в которые кузнечик попадает за один прыжок. Таких точек будет 5 · 6 + 1 = 31 — это вершины графа V, показанного на рисунке 14, в. Очевидно, точки P, Q, R образуют \( Δ_{\sqrt{3}} \). Пусть O — начало координат. При вычислении суммы Минковского V + V каждая точка будет складываться с точкой O, поэтому

{P, Q, R} ⊂ V ⊂ V + V ⊂ V + V + V.

Упражнение 4. а) Убедитесь, что если кузнечику разрешается сделать не более 2 прыжков, то ему доступны вершины графа W = V + V. б) Докажите, что W содержит веретено Мозеров в качестве подграфа.

Оказывается, что если отметить все точки, в которые кузнечик может попасть за 0, 1, 2 или 3 прыжка (V + V + V) и покрасить точки P, Q, R в один цвет, то правильно раскрасить остальные вершины в четыре цвета невозможно!

Искомый граф построен, но компьютерный перебор раскрасок затрагивает лишь небольшую часть вершин. Ди Грей не стал спешить с публикацией и попробовал сделать построение более экономным. Опишем вариант, к которому он пришел.

Пусть W′ состоит из векторов из W, длина которых не превосходит \( \sqrt{3} \). Пусть U — подграф V на 7 вершинах, показанный на рисунке 7.

Упражнение 5. Найдите мощности множеств W и W′.

Рис. 15. Граф H на 1345 вершинах

Граф H = W′ + U имеет 1345 вершин и является подграфом V + V + V (рис. 15). Если раскрасить в первый цвет три точки в вершинах \( Δ_{\sqrt{3}} \), выбранных из вершин U, компьютерный перебор показывает, что для раскраски остальных вершин четырех цветов (включая первый) не хватает.

Проверить это утверждение без написания программы пока никому не удалось. По сравнению со многими другими «компьютерными» доказательствами объем вычислений невелик: порядка минуты счета на одном ядре современного процессора. Но и этот перебор намного превышает человеческие возможности. А вот проверка с помощью компьютера доступна для большинства программистов.

Используется слегка усовершенствованный поиск в глубину. Во-первых, полезно вначале упорядочить вершины графа так, чтобы у следующей вершины было как можно больше соседей среди раскрашенных ранее (например, сортировкой по убыванию степени вершины, хотя есть способы и получше). Во-вторых, после раскраски какой-либо вершины следует сразу же проверять, нет ли среди соседних вершин таких, для которых остался только один вариант раскраски, и красить их немедленно (подобно тому, как сразу же вписываются единственные варианты при разгадывании судоку).

Плоские дистанционные графы с хроматическим числом 5

В предыдущих разделах мы описали построение графа G, при раскраске которого в 4 цвета хотя бы один из треугольников \( Δ_{\sqrt{3}} \) будет раскрашен в один цвет, и графа H, при раскраске которого в 4 цвета фиксированный треугольник \( Δ_{\sqrt{3}} \) не может быть одноцветным. Из первого условия следует, что на плоскости, раскрашенной в 4 цвета, найдется одноцветный \( Δ_{\sqrt{3}} \), а из второго — что одноцветного \( Δ_{\sqrt{3}} \) на плоскости нет. Это уже означает, что

\( χ (\mathbb{R}^2) ≥ 5 \),

но нетрудно указать и конкретный граф, обеспечивающий нижнюю оценку. Прикрепим к каждому из 52 шестиугольников в графе G по экземпляру H. При этом многие вершины совпадут, но это не должно нас беспокоить. Если не существует правильной раскраски графа в четыре цвета без учета их расположения на плоскости и отождествления вершин, то после отождествления ее тем более не будет. Полученный граф P на 20425 вершинах невозможно правильно раскрасить в четыре цвета.

Как и при переборе раскрасок H, выясняется, что большую часть вершин можно отбросить. Ди Грею удалось выделить из графа P подграф P′ на 1581 вершине, который также не красится в четыре цвета (рис. 16).

Рис. 16. Граф P′ на 1581 вершине. Не существует правильной раскраски P′ в четыре цвета

Статья ди Грея привлекла внимание энтузиастов комбинаторной геометрии к нескольким вопросам. Какое наименьшее число вершин может иметь плоский дистанционный граф с хроматическим числом 5 или больше? Нельзя ли найти граф с хроматическим числом 6 или 7, усложняя конструкцию? Существует ли доказательство новой нижней оценки, доступное для непосредственной проверки человеком?

Вскоре был найден алгоритмически более простой, хотя, увы, еще менее «человеческий» способ строить графы с хроматическим числом 5 и меньшим числом вершин. Выяснилось, что для этого можно взять в качестве множества вершин (V + V + V) ∪ φ_β (V + V + V), где φ_β — поворот на угол \( β = \text{arcsin} \frac{1}{8} \) вокруг начала координат. Автор статьи [6] перебирал различные способы отбрасывания «лишних» вершин при вычислении суммы Минковского, а затем использовал так называемые SAT-решатели², чтобы найти подграф, из которого нельзя удалить ни одной вершины без уменьшения хроматического числа. По состоянию на текущий момент удалось сократить число вершин до 553, но, разумеется, нет никакой гарантии, что это число минимально. Вполне вероятно, что рекорд еще не раз обновится. Его текущее значение можно узнать на сайте проекта Polymath [7] в разделе, посвященном данной задаче.

Литература
1. A. Soifer. The Mathematical Coloring Book. Springer, 2009.
2. А. Райгородский, О. Рубанов, В. Кошелев. Хроматические числа // Квант, 2008, №3.
3. А. М. Райгородский. Хроматические числа. М.: МЦНМО, 2015.
4. А. Я. Канель-Белов, В. А. Воронов, Д. Д. Черкашин. О хроматическом числе плоскости // Алгебра и анализ, 29:5 (2017), с. 68–89.
5. A. D. N. J. de Grey. The chromatic number of the plane is at least 5 // arXiv preprint arXiv:1804.02385 (2018).
6. M. J. H. Heule. Computing small unit-distance graphs with chromatic number 5 // arXiv preprint arXiv:1805.12181 (2018).
7. Проект Polymath.

¹ На рисунке 4 розовым выделена часть границы, окрашиваемая в тот же цвет, что и сам квадрат. Черная часть границы получает цвет от соседних квадратов.

² Специализированные алгоритмы и программы, предназначенные для решения задачи о выполнимости булевых формул — NP-полной задачи, к которой сводится в том числе и задача о раскраске графа в k цветов.