Песочная горка

Валерия Сирота
«Квантик» №10, 2019

Проходя мимо детской площадки, Мишка замедлил шаг. Малыши расползлись по углам, а в центре, у песочницы, шло недетское обсуждение. На углу деревянной рамы среди остатков былых куличиков лежал раскрытый номер «Квантика»^*. Миша подошёл поближе и прочитал:

Задача 1. Если аккуратно сыпать сверху сухой песок (из одной точки), получается ровная коническая горка. Измерьте зависимость высоты песчаной горки от радиуса её основания и нарисуйте график этой зависимости.

— ...вязальной спицей мерить! — говорила Лера. — Я у бабушки одолжу. Протыкаем горку спицей, потом к линейке прикладываем, так можно и диаметр, и высоту...

— Не годится, это тоже разрушающее измерение, — отверг идею Дима. — Ты спицей проткнёшь, горка просядет.

— Ну и что? Пускай проседает. Мы же уже измерим...

— Так за-ви-си-мость же надо измерить! А не только для одной какой-то горки. Штук семь хотя бы разных радиусов, и для каждого — высоту. Что же ты, каждый раз новую горку насыпать будешь? Лучше так — насыплем маленькую, измерим, подсыплем ещё, опять измерим... Только аккуратно измерять надо...

— Я и говорю — штангенциркуль нужен! — вставила Оля, похоже, уже не в первый раз.

— И где ты найдёшь этот свой циркуль? — спросил Дима, который, видимо, не знал, что это такое.

— Такой большой — нигде, — уверенно и мрачно заявил Костя.

— А может, прямо на линейку сыпать?

— Нет, тоже не очень: вдруг у нас горка перекосится немного, и будет не ровно круг, а мы будем измерять только один радиус. Или даже не совсем радиус, если центр сдвинется. Неточно получится.

— А может, миллиметровку вниз постелить?

— Или бумагу, большой лист, и каждый раз обводить карандашиком край горки, а потом уж радиусы измерим. Или наоборот, заранее круги нарисовать и сыпать песок, пока они не заполнятся.

— А высоту как измерять? Поставить заранее линейку вертикально? Но как закрепить?

— И это тоже будет разрушающее... Линейка симметрию нарушит. Может, всё-таки спицей?

Тут Мишка вмешался в разговор.

— Эй вы, экспериментаторы! Бросайте своё бесполезное занятие! Я и так знаю, какой ответ должен получиться.

Экспериментаторы обиделись, но решение выслушали.

— Действительно, очень просто, — сказала Лера. — Как же это мы сами-то...

— А вы сразу стали думать, как измерить, а что именно собираетесь измерять — подумать забыли! — назидательно сказал Мишка.

— Ну и что! — сказал Дима. — А эксперимент всё равно нужен. Мы им твою теорию проверим. Вдруг всё не так на самом деле? И вообще, как ты без измерений коэффициент трения узнаешь?

— Какой коэффициент трения?

— А ты читай внимательно, тут ещё задачи есть:

Задача 2. А как зависит от радиуса основания горки вес насыпанного песка?

Задача 3. Для старших — тех, кто уже начал изучать физику: как из этих измерений найти коэффициент трения песка о песок?

Здесь мы оставим эту компанию. Предлагаем вам повторить их подвиги: решить задачи теоретически, как Мишка, и понять, как должны выглядеть соответствующие графики, а потом проверить эти результаты экспериментально — или наоборот, сперва измерить и построить график, а потом уж разобраться, почему так. Рисовать график лучше на миллиметровке — будет гораздо точнее! Кстати, у ребят зависимость высоты горки от диаметра получилась не в точности такая, как предсказал Мишка, — никакой эксперимент не может быть абсолютно точным. Как вы думаете, для каких горок — больших или маленьких — точность их измерений была ниже?

Художник Мария Усеинова

Ответы

Рис. 1

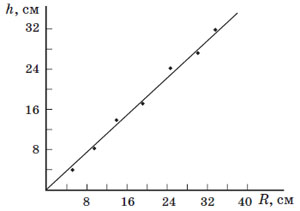
1. Мишка использовал идею подобия. Физические причины, определяющие форму горки, не зависят от ее размера — по крайней мере, для не очень больших горок, которые можно сделать в песочнице. Поэтому все горки подобны друг другу — у всех «крутизна склона» примерно одна и та же, все размеры отличаются в одно и то же число раз. Значит, высота прямо пропорциональна радиусу: на графике экспериментальные точки расположатся вдоль прямой линии, примерно как на рисунке 1.

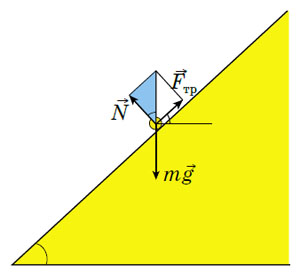
Рис. 2

2. Чтобы теоретически определить зависимость веса песка от радиуса горки, опять нужна идея подобия. Если одна горка по всем измерениям больше другой в 2 раза, то можно разделить их обе на воображаемые маленькие кубики (а по краешкам — другие кусочки, например половинки кубиков), и сторона каждого кубика первой горки будет больше стороны соответствующего кубика второй в 2 раза. А объем — в 2³ = 8 раз. Можно заменить в этом рассуждении 2 на R: объем любой горки прямо пропорционален кубу ее радиуса (или высоты), V = c · R³. Чтобы найти массу, умножим объем на плотность песка, получим M = m · R³. Здесь m и c — некоторые числа. Если у вас есть весы, можно это тоже проверить экспериментально и, построив график, сравнить его с теоретическим предсказанием: коэффициент m можно определить по одной из точек.

3. Ответ: от 0,7 до 0,9, в зависимости от степени сухости и сорта песка.

На песчинку, лежащую на склоне, действуют три силы: сила притяжения Земли (mg), направленная вниз, сила реакции опоры (N), направленная перпендикулярно поверхности, и сила трения (F_тр) — вдоль поверхности. (На самом деле сумма двух последних — это одна сила, действующая на песчинку со стороны остального песка.) Коэффициент трения — это отношение μ = F_тр/N. Чтобы песчинка не двигалась, сумма всех сил должна быть равна нулю, а значит, сумма векторов N и F_тр должна быть направлена вертикально вверх.

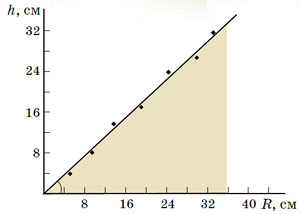
Рис. 3

Угол между N и вертикалью — такой же, как угол наклона горки (они получаются друг из друга поворотом картинки на 90°). Из подобия голубого и жёлтого треугольников получаем μ = F_тр/N = h/R — коэффициент трения равен отношению высоты горки к радиусу её основания. Его можно подсчитать для какой-нибудь одной из точек графика (одной горки) — но точнее взять среднее по всем измеренным горкам.

Между прочим, проведённая «посередине между точками» прямая линия на рисунке 1 имеет примерно тот же угол наклона, что и — в среднем — склоны песочных горок. Поэтому бежевый треугольник на рисунке 3 тоже подобен голубому и жёлтому на рисунке 2, а значит, можно измерить коэффициент трения и по нему; получится точнее, чем по одной какой-то точке.

^* Читатели «Квантика», угадайте — какой это был номер?