Чему смеялся Гельфанд
(Математическая новелла для нематематиков)

Е. Глаголева, В. Птушенко
«Квант» №4, 2013

2 сентября 2013 года исполнилось бы 100 лет Израилю Моисеевичу Гельфанду — одному из крупнейших ученых XX века.

В научном мире Гельфанд известен прежде всего как математик, оставивший свой след почти во всех областях современной математики. Знают его также биологи (курьезно, что, когда появились работы Гельфанда по биологии, некоторые специалисты интересовались, имеет ли этот биолог какое-либо отношение к знаменитому математику Гельфанду). И совсем почти неизвестен Гельфанд-педагог.

Впрочем, это неудивительно: он никогда не был педагогом-теоретиком, у него нет ни одной работы по педагогике. Его чрезвычайно интересные и, можно сказать, мудрые педагогические взгляды реализованы в его обширной многолетней деятельности. И, конечно, в его учениках.

Не слишком преувеличивая, можно сказать, что учениками Гельфанда становились все, кому доводилось с ним общаться. Будь то дело, сопровождающееся более-менее длительным общением, или единственный разговор, или даже простое присутствие при какой-то беседе — люди непременно в той или иной степени испытывали на себе его влияние.

А еще он одним из первых стал вести математический кружок для школьников при МГУ, принимал участие в организации первых московских математических олимпиад.

Но главный вклад Гельфанда в педагогику — это, несомненно, Заочная математическая школа (известная теперь как ВЗМШ), которая является в полной мере его детищем и которая была придумана и создана буквально с нуля.

Это было почти 50 лет назад. Мне довелось тогда работать с Израилем Моисеевичем. Я была первым «штатным» сотрудником Заочной школы, и это время было одно из самых трудных и счастливых в моей жизни.

Эта статья является последним поручением Израиля Моисеевича. Он жил тогда уже в Америке, и беседа шла в его кабинете в университете Ратгерса. Больше я с ним не встретилась. А Заочная школа выросла и продолжает работать, хотя формально ее не существует.

Е. Глаголева

С давних пор бытует такая легенда: будто бы однажды куда-то в глубинку в школу приехало какое-то начальство, а на уроке математики учитель объяснял ученикам правило сложения дробей. «Числитель первой дроби, — говорил учитель, — надо сложить с числителем второй, а знаменатель первой — со знаменателем второй». После урока удивленный «высокий гость» подошел к учителю и рассказал ему, как правильно надо складывать дроби. И следующий урок учитель начал словами: «Нас тут поправили: пришло новое указание из Центра, и теперь надо складывать дроби иначе».

Лет 15 назад этот анекдот кто-то рассказал во время беседы в кругу нескольких математиков, среди которых был Израиль Моисеевич Гельфанд. Один из авторов этой статьи, присутствовавший при разговоре, откликнулся на анекдот неожиданным для собеседников пассажем:

— Ну, а почему, собственно, нельзя так складывать дроби? Давайте введем такое правило сложения дробей и так и будем их складывать! Что нам мешает?

На это сейчас же последовало возражение:

— Но ведь тогда не будет выполняться распределительный закон!

— Ну, если при этом всё остальное оставить без изменения, то конечно! А мы изменим правило умножения дробей так, чтобы распределительный закон выполнялся, как и все остальные свойства сложения и умножения.

— Ну, ну, попробуйте! — еще больше удивились собеседники. — Интересно, как это Вам удастся!

В ответ на доске появилась формула:

Вот тут Гельфанд и засмеялся:

— Здорово! — сказал он. — Напишите про это. Вот мы и пишем.

Почему же смеялся Гельфанд?

Дело в том, что по правилу умножения Израиль Моисеевич узнал давно известные в математике и широко применяемые в разных областях числа, только наряженные в чужую одежду!

Поэтому сознаемся в этом «спектакле с переодеванием» и отметим, что запись «a/b» в нашем случае не означает, конечно, дробь, хотя бы потому, что дроби складываются и умножаются по другим правилам. Так что мы заменим «маскарадный костюм» каким-либо другим обозначением, например , а также вместо незаконно присвоенного названия «дроби» дадим другое, например «странные числа», или коротко «с-числа».

Но почему какие-то странные «дроби» можно считать числами? И откуда взялся этот самый распределительный закон, да и другие законы? И вообще:

А что мы называем числами?

Говоря попросту, числа — это то, что можно складывать и умножать, и чтобы при этом выполнялись некоторые правила — законы сложения и умножения, а именно:

a + b = b + a,   a · b = b · a,

(a + b) + c = a + (b + c),  (a · b) · c = a · (b · c),

a (b + c ) = ab + ac.

Эти требования выполняются для всех видов чисел, начиная с натуральных и кончая действительными.

Но почему так важны эти свойства чисел — в частности, именно такие, а не иные, законы сложения и умножения? Например, почему сумма непременно должна не меняться при перемене мест слагаемых, а произведение суммы на число должно быть обязательно равно сумме попарных произведений? И откуда вообще взялись эти правила?

Потрогать числа руками

Когда мы решаем любую задачу с помощью математики, мы используем вместо реальных предметов их математические образы. Но числа (точнее, натуральные числа) очень долго не отделялись от своих, так сказать, материальных носителей: люди считали не словами, а камушками, узелками, зарубками, в конце концов, пальцами.

Даже позже, когда уже появились натуральные числа, практические вычисления часто производились не на бумаге, а, например, на абаке или на русском его варианте — счетах. И числа можно было буквально потрогать руками, а действие законов было видно непосредственно. Действительно, если в одной корзине 100 яблок, а в другой 150, то необязательно ссыпать их в одну кучу и пересчитывать заново, чтобы узнать, сколько их всего. И поскольку число яблок не зависит от того, с какой корзины вы начнете их пересчитывать, то и результат сложения чисел не должен зависеть от порядка слагаемых.

При этом, естественно, в формулировке законов не было никакой нужды.

Не счетом единым...

Знакомство с новыми явлениями природы, развитие человеческой деятельности требовали новых математических образов. Для счета предметов было достаточно только натуральных чисел; когда же начались различного рода измерения — появились дроби.

Кроме того, числа из простого инструмента человеческой практики стали предметом научного исследования, и стало ясно, что в построении системы чисел должна быть своя логика, внутренняя согласованность разных свойств этой системы, их взаимная непротиворечивость. Вряд ли в практике кому-то могло быть нужным знать, что получится, если 2 разделить на ноль. А вот в Индии уже в VII веке об этом спорили: некоторые математики считали, что x : 0 = х, так как «разделить на ноль — это значит ни на что не разделить, поэтому останется то, что было»! Попробуйте-ка опровергнуть это высказывание, не задумываясь о взаимосвязи разных свойств чисел, т. е. о теории чисел! Можно, конечно, сказать, что делить на ноль — это не «ни на что не разделить», а «разделить на ничто», но это справедливо будет расценено как игра словами, не проясняющая сути вопроса. В таких вопросах интуиции, основанной на практике, на прямом наблюдении, в ряде случаев было уже недостаточно.

Да и до сих пор нередко наши интуитивные представления вступают в противоречие с математическими закономерностями. И сейчас бывает, что люди удивляются: «Как это так: мы умножаем число «двадцать» на одну вторую и получаем десять? Умножать — значит увеличивать, а получается меньше». А ответ на вопрос: «Что больше — пять процентов от трех или три процента от пяти?» далеко не всегда очевиден даже для школьников, поступающих в математический класс, а ведь этот ответ — прямое следствие коммутативного закона умножения.

С отрицательными числами не проще: хотя имеется хорошее истолкование отрицательных чисел как «долга», в отличие от положительных, означающих «прибыль», всё равно отрицательные числа кажутся менее естественными, чем дроби. Что такое половина яблока или треть стакана воды, может видеть или вообразить себе каждый. А кто когда-нибудь держал в руках «минус три рубля»? А уж правила действий! «Что плюс на плюс дает плюс — это правильно; что плюс на минус будет минус — это может быть, но чтобы минус на минус давал плюс — это ты врешь!»¹ Неудивительно, что мы до сих пор часто в быту обходимся без отрицательных чисел, говоря, например, «восемь градусов мороза» вместо «минус 8 градусов» или «у меня 3 тысячи рублей долгу» вместо «у меня минус 3 тысячи рублей».

Назвался груздем — полезай в кузов!

Итак, свойства чисел и действий над ними отчасти определяются свойствами тех физических объектов или процессов, которые они призваны описывать, отчасти же — вытекают из необходимости построить непротиворечивую, внутренне согласованную систему. Непротиворечивость же и внутренняя согласованность так же необходима для математического аппарата, как согласованность между собой движений всех деталей любой машины — без нее она просто не будет работать.

Эта непротиворечивость обеспечивается тем, что все правила обращения с числами и с буквенными, т. е. алгебраическими, выражениями следуют из тех пяти законов, которые мы привели выше. В этом смысле они играют в алгебре ту же роль, что и геометрические аксиомы, и, требуя их выполнения для каких-то новых чисел, мы получаем «гарантию», что новое не испортит старое, что со всеми числами можно будет обращаться по единым правилам.

Собственно говоря, мы только тогда и сможем называть новое число «числом», когда убедимся, что оно удовлетворяет всем требованиям, общим для чисел, известных ранее. Пословица: «Хоть горшком назови, только в печь не ставь» неприменима в математике; здесь гораздо больше подходит другая: «Назвался груздем — полезай в кузов!» В математике уж если что-то назвали горшком, то это можно ставить в печь. Если что-то названо «числом» (или «вектором», или «функцией», или «альфа-бета-гамма-абракадаброй»), то будьте уверены — с ним можно будет выполнять все действия и оно будет обладать всеми свойствами, характерными для данного типа математических объектов.

Странные, но всё же — числа

Поэтому, не веря на слово, прежде чем называть странные дроби числами, хотя и странными, нужно было бы аккуратно проверить выполнение всех пяти законов. Мы проверим только два из них, предоставив читателю проверить остальные самостоятельно.

1) Переместительный закон (коммутативность) для сложения: . В самом деле

Здесь среднее равенство верно, поскольку коммутативный закон справедлив для сложения действительных чисел (и над, и под чертой совершаются действия с «обычными» вещественными числами), а крайние знаки равенства верны в силу нашего определения операции сложения «странных чисел».

2) Распределительный закон (дистрибутивность): В самом деле:

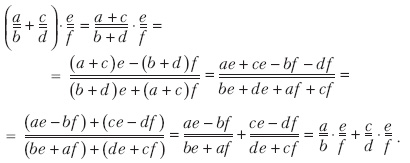
В этой цепочке равенств использованы все пять свойств действий с действительными числами. Что же мы получили?

Нули и единицы

Итак, формальное требование соблюдено: введенные нами с-числа подчиняются законам, обязательным для всех чисел.

Теперь попробуем «повертеть в руках» эти новые числа, посмотреть, чем они похожи на известные нам действительные числа, чем от них отличаются, как происходят с ними различные действия, всегда ли выполняются обратные действия, есть ли среди этих чисел ноль и единица и т. д.

Кстати: а что такое ноль?

Легче всего получить ноль вычитанием:

z – z = 0.

Это верно для любого числа z. Другими словами, при любом z будет верно равенство

z + 0 = z,

т. е. ноль — это такое число, от прибавления которого к любому числу оно не меняется. Это равенство можно считать определением числа ноль.

Легко понять, что среди с-чисел роль нуля играет число . Действительно:

Теперь поищем единицу. Единица — это для умножения то же, что ноль для сложения, т. е. число, от умножения на которое никакое число не меняется: если для любого числа то можно назвать единицей среди с-чисел. Легко показать, что x = 1, y = 0, т. е. роль единицы для с-чисел играет число .

Действительные и странные: протянем связующие ниточки

Теперь посмотрим, как множество с-чисел связано с множеством «обычных», т. е. действительных, чисел? Воспользуемся тем, что любое с-число можно разбить на два слагаемых (по правилу сложения с-чисел):

Рассмотрим первое слагаемое. Оказывается, числа вида ведут себя в точности так, как самые обыкновенные действительные числа: сумма и произведение таких чисел будет числом того же рода, так как

при этом и сложение, и умножение (и обратные к ним операции) происходят по «обычным» правилам (как у «обычных» действительных чисел, если не считать приписанного в конце каждого числа нолика под чертой). И, что очень важно, и нулевой, и единичный элементы с-чисел также будут среди этих чисел вида , т. е. и «ноль», и «единица» у с-чисел и у действительных чисел оказываются общими! Поэтому мы «числа» вида смело можем обозначать просто a. Тогда число представится в виде суммы .

Рассмотрим теперь второе слагаемое, т. е. число вида . Легко убедиться, что сложение таких чисел дает число того же рода:

Получается, что с-числа складываются (и вычитаются) «почленно»: действительные слагаемые с действительными, а странные — со странными. Естественно: ведь мы и хотели, чтобы при сложении «дробей» складывались «числители» и «знаменатели».

С умножением дело сложнее, придется рассмотреть разные ситуации.

Сначала посмотрим, как умножается с-число вида на действительное число. Для этого надо в формуле, задающей правило умножения с-чисел, положить a = 0 и d = 0. Получим

т. е. от умножения с-числа с нулевым «числителем» на действительное получается с-число. Тогда любое с-число можно представить как произведение действительного числа b на число :

.

Получается, что число , так сказать, порождает все с-числа, подобно тому как единица порождает все действительные. Поэтому назовем (временно) это число «с-единицей» и обозначим его так: 1_c.

Теперь всякое с-число можно будет записать в виде

Здесь a и b — действительные числа, «+» — знак сложения, b·1_c — произведение действительного числа b на с-единицу, т. е. с-число .

Такая форма очень удобна для с-чисел: в этой форме с ними можно обращаться по всем правилам алгебры, так как мы проверили, что все законы соблюдены, а правила алгебры следуют из этих законов. Поэтому мы можем теперь перемножить два с-числа, записанных в такой форме, по правилу умножения многочленов.

Неожиданный результат

Чтобы закончить с умножением с-чисел, нам остается проверить, что получается при умножении двух с-чисел вида . Поскольку, как мы только что показали, каждое число можно представить в виде произведения действительного числа и с-единицы, то достаточно проверить, чему равен квадрат с-единицы, т. е. (1_c)² . Возьмем число и умножим само на себя:

Вот здесь можно закричать: караул! Квадрат с-числа оказался действительным отрицательным числом! Вот это, действительно, совсем новое и (как мы увидим уже скоро) очень важное свойство с-чисел (среди действительных чисел, как мы помним, ничего похожего не встречалось).

Итак, . Заменив в следующем равенстве (1_c)² на -1, получим

(a + b · 1_c) · (c + d · 1_c) = ac + ad · 1_c + bc · 1_c + bd · (1_c)² = ac – bd + (ad + bc) · 1_c.

Если эту формулу записать в старых обозначениях, где действительное слагаемое стоит в «числителе», а странное — в «знаменателе», т. е. заменить a + b · 1_c на , c + d · 1_c на и ac – bd + (ad + bc) · 1_c на , то мы и получим то правило умножения, которое было предложено в беседе с Гельфандом:

Снимем маски

Теперь станет понятно, почему Гельфанда не обманула наша маскировка. Освободимся от нее и мы и возвратим с-числам их собственную «одежду» — обозначение и наименование, которые употребляются в математике.

На самом деле с-единица называется не «странной» единицей, а мнимой и обозначается буквой i (от слова imaginarius — мнимый). Соответственно, наши странные числа bi называются мнимыми, а числа вида a + bi, где i = –1, называются комплексными числами.

Ясно, что множество комплексных чисел содержит в себе все действительные числа (если b = 0) и все мнимые числа (если a = 0).²

Откуда взялись комплексные числа?

Итак, эти новые числа содержат число, квадрат которого отрицателен: i² = –1 . Это и в самом деле новые числа, таких чисел среди действительных нет.

Ясно, что «из опыта» такие числа не могли возникнуть — ведь даже отрицательные числа не очень-то спокойно воспринимались математиками, поскольку трудно себе представить «отрицательные» предметы реального мира. А комплексные числа — это нечто еще более «экзотическое», чему еще труднее найти соответствие в «реальном» мире.

Разумеется, здесь на первый план выступают «внутриматематические» потребности. В частности, с развитием математики появился новый стимул для введения новых чисел: выполнимость обратных операций. Так, введение отрицательных чисел и нуля обеспечило выполнимость вычитания, а введение дробей — деления. (Правда, для деления осталось существенное ограничение: деление на ноль невозможно. Но это ограничение только подчеркивает, что в математике нельзя делать всё что угодно: новое не должно противоречить всему, ранее сделанному и доказанному.) Благодаря введению комплексных чисел становится всегда возможным действие, обратное к возведению в степень.

Но появились комплексные числа в математике совсем по другому поводу. Это было в XVI веке. Среди математиков того времени были распространены разные соревнования, конкурсы (иногда публичные, вроде современных матбоев) по решению трудных задач. Одной из таких задач было нахождение общей формулы решения кубических уравнений. Итальянский математик Кардано (он был также медиком и инженером: карданный вал — это его работа) при решении этой задачи столкнулся с удивительным фактом. Один из подходов к решению кубических уравнений состоял в том, чтобы с помощью подстановок свести кубическое уравнение к квадратному, способ решения которого был уже известен, а затем через полученные корни квадратного выразить искомые корни кубического. При этом тогда, разумеется, считалось, что квадратное уравнение при отрицательном дискриминанте не имеет корней. Казалось, естественно было бы, что если вспомогательное квадратное уравнение корней не имеет, то и соответствующее кубическое тоже их не имеет.

Но неожиданно оказалось, что именно в том случае, когда дискриминант вспомогательного уравнения отрицателен, (т. е. под знаком квадратного корня стоит отрицательная величина), исходное кубическое уравнение не только имеет корень или два, но имеет три различных действительных корня! Чтобы вычислить эти корни, приходилось оперировать с квадратными корнями из отрицательных чисел. И тут Кар-дано сделал смелый шаг: он обозначил «неизвлекающийся» корень из -1 буквой i.

Эту ситуацию можно уподобить движению по извилистой дороге. Мы можем «перепрыгнуть» с одной ее петли на другую; при этом, сойдя с дороги, мы, в конечном итоге, опять вернемся на нее. Точки пространства, окружающего нитку дороги, идущей через бескрайние поля или леса, могут не интересовать движущегося по дороге путника сами по себе, могут быть непреодолимы без специальных транспортных средств, могут даже показаться «ненастоящими» и ненужными (на них ведь не стоят верстовые столбы, и перемещаться из города в город они не помогают). Но если по ним всё же возможно как-то двигаться, то они позволяют существенно «срезать» дорогу.

Тем не менее, эти «ненастоящие» точки вокруг «действительных» со временем также оказались и весьма интересными сами по себе, и даже не столь уж «ненастоящими». Для них нашлись прообразы в «реальном» мире, и для описания этих прообразов комплексные числа впоследствии очень пригодились. Среди этих прообразов оказались, например, маятники и волны. А поскольку еще с первых шагов квантовой физики стало ясно, что вся материя обладает волновыми свойствами, то можно сказать, что комплексные числа окружают нас повсюду.

А главное, комплексные числа внесли определенную гармонию в математические представления. Так, например, при решении алгебраических уравнений в действительных числах мы постоянно сталкиваемся с вопросом: имеет ли данное уравнение корни, и если да, то сколько? Для разных уравнений ответы на эти вопросы могут быть различными. А при введении комплексных чисел всё становится красиво и закономерно: каждое алгебраическое уравнение n-й степени имеет ровно n корней. И это — только один пример.

С миру по нитке — голому куча ниток

Как вы помните, автору статьи, предложившему Гельфанду складывать дроби по «правилу» числитель с числителем, знаменатель со знаменателем, «пригрозили» невыполнением распределительного закона (или других законов).

Другой автор статьи со свойственной ему дотошностью решил проверить, в чем именно состоит это нарушение закона. И тут случился казус! Оказывается, что если принять «правило» сложения и не менять правило умножения, то все законы действий прекрасно себе выполняются.

Что же получается? А получается то, что такие «дроби» тоже можно считать числами!

На первый взгляд, кажется непонятным, почему же такой простой объект «не попал» в математику, почему математики обошли его вниманием, введя вместо него совсем другие, более сложные правила обращения с парами чисел? Но приглядитесь внимательно к этим простым правилам сложения и умножения: ни при каких операциях «числители» и «знаменатели» таких «дробей» не «перемешиваются»! «Числитель» результата будет зависеть только от «числителей» слагаемых или сомножителей, а «знаменатель» — только от «знаменателей». Числитель и знаменатель такой дроби «живут» каждый своею собственной жизнью — жизнью «обычного» множества целых чисел. В каждом из этих двух «миров» (над чертой и под чертой) будет свой ноль, своя единица — в точности такие же, какие есть в мире целых чисел.

Такая конструкция не дает ничего нового: это по-прежнему действительные числа, просто теперь «ходящие» парами. Вспомним, что рациональные числа — это принципиально новые объекты по отношению к целым числам, точно так же, как комплексные — по отношению к вещественным: введение первых позволило решать любые линейные уравнения, введение вторых — алгебраические уравнения любых степеней. В нашем же примере произошло примерно то же, что сказано в шутке в заголовке этого параграфа: совокупность ниток оказалась не рубашкой, а просто кучей ниток...

«А мы чем хуже?», или Почему векторы — не числа?

В заключение скажем пару слов еще об одном математическом объекте, похожем на только что рассматривавшиеся нами: о двумерных векторах. Ведь это тоже упорядоченные пары чисел! Почему же они не считаются числами? Чем они хуже комплексных чисел? Сложение двумерных векторов действительно очень похоже на сложение комплексных чисел — оно тоже почленное: первое число (в случае вектора оно называется компонентой) складывается с первым, второе — со вторым. Здесь сходство налицо. Можно добавить, что комплексные числа часто изображают двумерными векторами на так называемой комплексной плоскости.

Однако на этом сходство и заканчивается: у векторов нет умножения. Так называемое скалярное произведение двух векторов не является вектором — а ведь это основное требование к операции умножения тех объектов, которые можно назвать числами: чтобы она давала объект той же природы, что и сомножители. Правда, в векторной алгебре вводят еще и векторное произведение двух векторов, и его результатом является снова вектор. Но, во-первых, оно существует для векторов в пространстве, т. е. имеющих три компоненты. А, во-вторых, оно не удовлетворяет коммутативному закону. Почему (и зачем)? — это тема отдельного разговора, далеко выходящего за пределы той математической шутки, о которой просил написать Гельфанд.

---

¹ Из книги Ивана Василенко «Рассказы об Артемке. Артемка у гимназистов».
² Числа вида bi иногда называют чисто мнимыми.