Моделирование критических явлений в популяциях лесных насекомых

Фото с сайта https://lessad.ru/blog/sosnovy-shelkopryad-atakuet-lesa-rossii

Моделирование и прогнозирование динамики численности популяций часто включает анализ многих факторов, что затрудняет реальное их применение. В настоящей работе предпринята попытка построения минималистских моделей динамики численности насекомых, использующих только данные по плотности изучаемого вида без точного знания характеристик регулирующих и модифицирующих факторов. Для моделирования такого критического явления, как вспышка массового размножения насекомых, мы используем два подхода – описание экологических процессов как аналогов фазовых переходов в физических системах и как аналогов экономических процессов, в которых текущее состояние системы зависит от ее прошлых состояний.

Наверное, нет области знаний, в которой не изучались бы критические явления. Эти процессы, связанные с качественными изменениями состояния изучаемых объектов, наблюдаются в физике, химии, экономике, биологии, экологии, психологии. Так, в физике хорошо известно, что под влиянием изменений внешний среды – например, изменения ее температуры, – могут происходить такие критические явления, как кипение и скачкообразный переход физической системы из жидкого в газообразное состояние (фазовый переход первого рода) или появлении у вещества новых свойств – магнитного момента или сверхтекучести (фазовый переход второго рода). В экологии примером критических явлений являются смена древесных пород в насаждении, пожары, вспышки массового размножения насекомых. В медицине самое важное критическое явление – болезнь и смерть. Можно говорить об общих системных свойствах критических явлений и сравнивать эти общие свойства для разных систем. В представленных работах с общих позиций рассматривались модели таких критических явлений, как вспышки массового размножения лесных насекомых рода Dendrolimus (например, сибирский и сосновый шелкопряды) и эпидемия коронавируса на нашей планете в 2020 г.

Рис. 1. Квадрат w² доли штатов и территорий США (по данным Университета Дж. Гопкинса; Johns Hopkins University, 2020), в которых на дату t не наблюдалось больных COVID19: 1 – начальная стадия эпидемии (три штата, 2 – латентный период эпидемии, 3 – стадия массового заражения, 4 – эпидемии по всей территории США.

В этих работах показано, что критические явления в биологических и экологических системах можно моделировать как аналоги моделей фазовых переходов в физических системах. Это означает, что такие системы характеризуются наличием отрицательных обратных связей, позволяющих поддерживать систему в стабильном (метастабильном) состоянии и положительных обратных связей, перебрасывающих систему из одного устойчивого состояния в другое. Существование критических явлений – обязательное свойство бистабильной системы.

Можно говорить о пороговом характере возникновения критических явлений и наличие критических значений характеристик системы, при достижении которых начинаются качественные изменения в системе. Эти процессы можно описать как аналоги фазовых переходов первого рода в физических системах. Согласно этим моделям, можно говорить о существовании как минимум двух стабильных или метастабильных состояний систем, характеризуемых колебаниями характеристик состояния вблизи некоторого значения каждого из состояний и о наличии потенциального барьера, препятствующего перебросу системы из одного состояния в другое. Чем выше значение потенциального барьера, тем меньше вероятность реализации критического явления.

Классические» модели вирусных эпидемий (Kermack, McKendrick A., 1927) - беспороговые, то есть допускается возможность развития эпидемии после единичного случая заболевания, однако в наших работах рассмотрены бистабильные модели с критическими пороговыми значениями и для плотности популяции насекомых, и для числа заболевших коронавирусом.

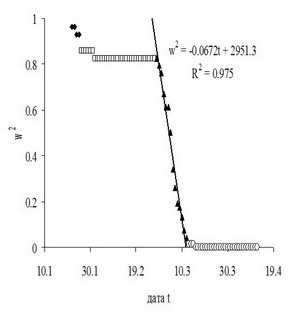
Если ввести понятие параметра порядка как некоторого обобщенного показателя состояния системы, то описать изменения состояния системы можно, используя аналоги уравнения Л.Д.Ландау (1937) для фазовых переходов второго рода как для процесса распространения эпидемии коронавируса по территории, так и для распределения гусениц насекомых по деревьям в насаждении (рис.1 и 2).

Рис. 2. Связь между квадратом доли неповрежденных деревьев q² и логарифмом плотности х популяций сибирского шелкопряда в очагах массового размножения в 1953–1969 гг.: 1 – плотности популяции ниже критической плотности освоения деревьев вредителями x _m ; 2 – плотности популяции выше критической плотности освоения x _m .

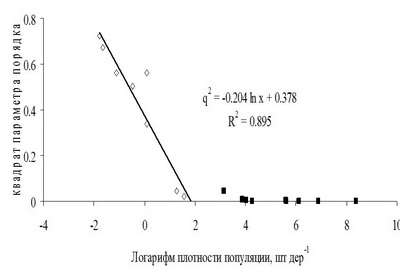
В физике в рамках теории фазовых переходов вводится принцип универсальности, согласно которому процессы фазовых переходов зависят только от некоторых основных свойств систем, таких как размерность, число компонентов у параметра состояния системы, зависимость взаимодействия в системе от расстояния (Брус, Каули, 1984). Использование идеи универсальности фазовых переходов упрощает и унифицирует построение моделей фазовых переходов. Даже не зная точного вида функции состояния системы, все же можно описать процесс фазового перехода и найти критические значения внешнего фактора и значения параметров в устойчивых состояниях системы. И эти свойства моделей критических явлений использованы в описанных работах.